
SL Paper 3
Observer A detects the creation (event 1) and decay (event 2) of a nuclear particle. After creation, the particle moves at a constant speed relative to A. As measured by A, the distance between the events is 15 m and the time between the events is 9.0 × 10–8 s.
Observer B moves with the particle.
For event 1 and event 2,
Explain what is meant by the statement that the spacetime interval is an invariant quantity.
calculate the spacetime interval.
determine the time between them according to observer B.
Outline why the observed times are different for A and B.
Rocket A and rocket B are travelling in opposite directions from the Earth along the same straight line.
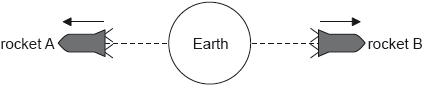
In the reference frame of the Earth, the speed of rocket A is 0.75c and the speed of rocket B is 0.50c.
Calculate, for the reference frame of rocket A, the speed of rocket B according to the Galilean transformation.
Calculate, for the reference frame of rocket A, the speed of rocket B according to the Lorentz transformation.
Outline, with reference to special relativity, which of your calculations in (a) is more likely to be valid.
The diagram shows the motion of the electrons in a metal wire carrying an electric current as seen by an observer X at rest with respect to the wire. The distance between adjacent positive charges is d.

Observer Y is at rest with respect to the electrons.
State whether the field around the wire according to observer X is electric, magnetic or a combination of both.
Discuss the change in d according to observer Y.
Deduce whether the overall field around the wire is electric, magnetic or a combination of both according to observer Y.
Identical twins, A and B, are initially on Earth. Twin A remains on Earth while twin B leaves the Earth at a speed of 0.6c for a return journey to a point three light years from Earth.
Calculate the time taken for the journey in the reference frame of twin A as measured on Earth.
Determine the time taken for the journey in the reference frame of twin B.
Draw, for the reference frame of twin A, a spacetime diagram that represents the worldlines for both twins.
Suggest how the twin paradox arises and how it is resolved.
Muons are created in the upper atmosphere of the Earth at an altitude of 10 km above the surface. The muons travel vertically down at a speed of 0.995c with respect to the Earth. When measured at rest the average lifetime of the muons is 2.1 μs.
Calculate, according to Galilean relativity, the time taken for a muon to travel to the ground.
Deduce why only a small fraction of the total number of muons created is expected to be detected at ground level according to Galilean relativity.
Calculate, according to the theory of special relativity, the time taken for a muon to reach the ground in the reference frame of the muon.
Discuss how your result in (b)(i) and the outcome of the muon decay experiment support the theory of special relativity.
This question is about simultaneity.
Daniela is standing in the middle of a train that is moving at a constant velocity relative to Jaime, who is standing on the platform. At the moment the train passes Jaime, two beams of light, X and Y, are emitted simultaneously from a device held by Daniela. Both beams are reflected by mirrors at the end of the train and then return to Daniela.

State and explain the order of arrival of X and Y at the mirrors according to Jaime.
Outline whether the return of X and Y to Daniela are simultaneous according to Jaime.
A long current-carrying wire is at rest in the reference frame S of the laboratory. A positively charged particle P outside the wire moves with velocity v relative to S. The electrons making up the current in the wire move with the same velocity v relative to S.
State what is meant by a reference frame.
State and explain whether the force experienced by P is magnetic, electric or both, in reference frame S.
State and explain whether the force experienced by P is magnetic, electric or both, in the rest frame of P.
This question is about a Galilean transformation and time dilation.
Ben is in a spaceship that is travelling in a straight-line with constant speed \(v\) as measured by Jill who is in a space station.
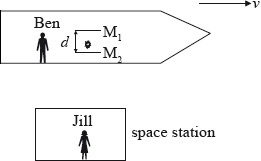
Ben switches on a light pulse that bounces vertically (as observed by Ben) between two horizontal mirrors \({{\text{M}}_{\text{1}}}\) and \({{\text{M}}_{\text{2}}}\) separated by a distance \(d\). At the instant that the mirrors are opposite Jill, the pulse is just leaving the mirror \({{\text{M}}_{\text{2}}}\). The speed of light in air is \(c\).
The time for the light pulse to travel from \({{\text{M}}_{\text{2}}}\) to \({{\text{M}}_{\text{1}}}\) as measured by Jill is \(\Delta t\).
On the diagram, sketch the path of the light pulse between \({{\text{M}}_{\text{1}}}\) and \({{\text{M}}_{\text{2}}}\) as observed by Jill.

(i) State, according to Jill, the distance moved by the spaceship in time \(\Delta t\).
(ii) Using a Galilean transformation, derive an expression for the length of the path of the light between \({{\text{M}}_{\text{2}}}\) and \({{\text{M}}_{\text{1}}}\).
State, according to special relativity, the length of the path of the light between \({{\text{M}}_{\text{1}}}\) and \({{\text{M}}_{\text{1}}}\) as measured by Jill in terms of \(c\) and \(\Delta t\).
The time for the pulse to travel from \({{\text{M}}_{\text{2}}}\) to \({{\text{M}}_{\text{1}}}\) as measured by Ben is \(\Delta t'\). Use your answer to (b)(i) and (c) to derive a relationship between \(\Delta t\) and \(\Delta t'\).
According to a clock at rest with respect to Jill, a clock in the spaceship runs slow by a factor of 2.3. Show that the speed \(v\) of the spaceship is 0.90c.
This question is about relativistic kinematics.
A spacecraft is flying in a straight line above a base station at a speed of 0.8c.
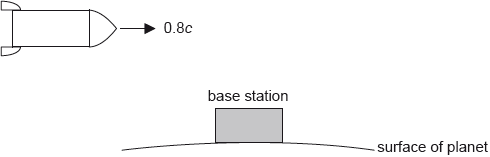
Suzanne is inside the spacecraft and Juan is on the base station.
While moving away from the base station, Suzanne observes another spacecraft travelling towards her at a speed of 0.8c. Using Galilean transformations, calculate the relative speed of the two spacecraft.
Using the postulates of special relativity, state and explain why Galilean transformations cannot be used in this case to find the relative speeds of the two spacecraft.
Using relativistic kinematics, the relative speeds of the two spacecraft is shown to be 0.976c. Suzanne measures the other spacecraft to have a length of 8.00 m. Calculate the proper length of the other spacecraft.
Suzanne’s spacecraft is on a journey to a star. According to Juan, the distance from the base station to the star is 11.4 ly. Show that Suzanne measures the time taken for her to travel from the base station to the star to be about 9 years.
Muons are unstable particles with a proper lifetime of 2.2 μs. Muons are produced 2.0 km above ground and move downwards at a speed of 0.98c relative to the ground. For this speed \(\gamma \) = 5.0. Discuss, with suitable calculations, how this experiment provides evidence for time dilation.
An electron is emitted from a nucleus with a speed of 0.975c as observed in a laboratory. The electron is detected at a distance of 0.800m from the emitting nucleus as measured in the laboratory.
For the reference frame of the electron, calculate the distance travelled by the detector.
For the reference frame of the laboratory, calculate the time taken for the electron to reach the detector after its emission from the nucleus.
For the reference frame of the electron, calculate the time between its emission at the nucleus and its detection.
Outline why the answer to (c) represents a proper time interval.
Define proper length.
A charged pion decays spontaneously in a time of 26 ns as measured in the frame of reference in which it is stationary. The pion moves with a velocity of 0.96c relative to the Earth. Calculate the pion’s lifetime as measured by an observer on the Earth.
In the pion reference frame, the Earth moves a distance X before the pion decays. In the Earth reference frame, the pion moves a distance Y before the pion decays. Demonstrate, with calculations, how length contraction applies to this situation.
Outline the conclusion from Maxwell’s work on electromagnetism that led to one of the postulates of special relativity.
One of the postulates of special relativity states that the laws of physics are the same in all inertial frames of reference.
State what is meant by inertial in this context.
An observer is travelling at velocity v towards a light source. Determine the value the observer would measure for the speed of light emitted by the source according to
(i) Maxwell’s theory.
(ii) Galilean transformation.
This question is about relativistic kinematics.
The diagram shows a spaceship as it moves past Earth on its way to a planet P. The planet is at rest relative to Earth.

The distance between the Earth and planet P is 12 ly as measured by observers on Earth. The spaceship moves with speed 0.60c relative to Earth.
Consider two events:
Event 1: when the spaceship is above Earth
Event 2: when the spaceship is above planet P
Judy is in the spaceship and Peter is at rest on Earth.
Judy considers herself to be at rest. According to Judy, the Earth and planet P are moving to the left.
State the reason why the time interval between event 1 and event 2 is a proper time interval as measured by Judy.
(i) Calculate the time interval between event 1 and event 2 according to Peter.
(ii) Calculate the time interval between event 1 and event 2 according to Judy.
(i) Calculate, according to Judy, the distance separating the Earth and planet P.
(ii) Using your answers to (b)(ii) and (c)(i), determine the speed of planet P relative to the spaceship.
(iii) Comment on your answer to (c)(ii).
Determine, according to Judy in the spaceship, which signal is emitted first.
This question is about a light clock.
One of the postulates of special relativity refers to the speed of light. State the other postulate of special relativity.
This question is about relativistic kinematics.
An observer at rest relative to Earth observes two spaceships. Each spaceship is moving with a speed of 0.85 c but in opposite directions. The observer measures the rate of increase of distance between the spaceships to be 1.7 c. Outline whether this observation contravenes the theory of special relativity.
The observer on Earth in (a) watches one spaceship as it travels to a distant star at a speed of 0.85 c. According to observers on the spaceship, this journey takes 8.0 years.
(i) Calculate, according to the observer on Earth, the time taken for the journey to the star.
(ii) Calculate, according to the observer on Earth, the distance from Earth to the star.
(iii) At the instant when the spaceship passes the star, the observer on the spaceship sends a radio message to Earth. The spaceship continues to move at a speed of 0.85 c. Determine, according to the spaceship observer, the time taken for the message to arrive on Earth.
State one prediction of Maxwell’s theory of electromagnetism that is consistent with special relativity.
A current is established in a long straight wire that is at rest in a laboratory.
A proton is at rest relative to the laboratory and the wire.
Observer X is at rest in the laboratory. Observer Y moves to the right with constant speed relative to the laboratory. Compare and contrast how observer X and observer Y account for any non-gravitational forces on the proton.
Two protons are moving with the same velocity in a particle accelerator.
Observer X is at rest relative to the accelerator. Observer Y is at rest relative to the protons.
Explain the nature of the force between the protons as observed by observer X and observer Y.
This question is about simultaneity.
State the postulate of special relativity that is related to the speed of light.
A rocket moving at a relativistic speed passes an observer who is at rest on the ground equidistant from two trees L and R. At the moment that an observer in the rocket is opposite the ground observer, lightning strikes L and R at the same time according to the
ground observer. Light from the strikes reaches the observer in the rocket as well as the observer on the ground.
(i) Explain why, according to the observer in the rocket, light from the two strikes will reach the ground observer at the same time.
(ii) Using your answer to (a) and (b)(i), outline why, according to the rocket observer, tree R was hit by lightning before tree L.
A train is passing through a tunnel of proper length 80 m. The proper length of the train is 100 m. According to an observer at rest relative to the tunnel, when the front of the train coincides with one end of the tunnel, the rear of the train coincides with the other end of the tunnel.
Explain what is meant by proper length.
Draw a spacetime diagram for this situation according to an observer at rest relative to the tunnel.
Calculate the velocity of the train, according to an observer at rest relative to the tunnel, at which the train fits the tunnel.
For an observer on the train, it is the tunnel that is moving and therefore will appear length contracted. This seems to contradict the observation made by the observer at rest to the tunnel, creating a paradox. Explain how this paradox is resolved. You may refer to your spacetime diagram in (b).
This question is about time dilation.
Two space stations X and Y are at rest relative to each other. The separation of X and Y as measured in their frame of reference is 1.80×1011m.
State what is meant by a frame of reference.
A radio signal is sent to both space stations in (a) from a point midway between them. On receipt of the signal a clock in X and a clock in Y are each set to read zero. A spaceship S travels between X and Y at a speed of 0.750c as measured by X and Y. In the frame of reference of S, station X passes S at the instant that X’s clock is set to zero. A clock in S is also set to zero at this instant.
(i) Calculate the time interval, as measured by the clock in X, that it takes S to travel from X to Y.
(ii) Calculate the time interval, as measured by the clock in S, that it takes S to travel from X to Y.
(iii) Explain whether the clock in X or the clock in S measures the proper time.
(iv) Explain why, according to S, the setting of the clock in X and the setting of the clock in Y does not occur simultaneously.
Two rockets, A and B, are moving towards each other on the same path. From the frame of reference of the Earth, an observer measures the speed of A to be 0.6c and the speed of B to be 0.4c. According to the observer on Earth, the distance between A and B is 6.0 x 108 m.
Define frame of reference.
Calculate, according to the observer on Earth, the time taken for A and B to meet.
Identify the terms in the formula.
u′ = \(\frac{{u - v}}{{1 - \frac{{uv}}{{{c^2}}}}}\)
Determine, according to an observer in A, the velocity of B.
Determine, according to an observer in A, the time taken for B to meet A.
Deduce, without further calculation, how the time taken for A to meet B, according to an observer in B, compares with the time taken for the same event according to an observer in A.
This question is about relativity.
Carrie is in a spaceship that is travelling towards a star in a straight-line at constant velocity as observed by Peter. Peter is at rest relative to the star.
Carrie measures her spaceship to have a length of 100m. Peter measures Carrie’s spaceship to have a length of 91m.
(i) Explain why Carrie measures the proper length of the spaceship.
(ii) Show that Carrie travels at a speed of approximately 0.4 c relative to Peter.
According to Carrie, it takes the star ten years to reach her. Using your answer to (a)(ii), calculate the distance to the star as measured by Peter.
According to Peter, as Carrie passes the star she sends a radio signal. Determine the time, as measured by Carrie, for the message to reach Peter.
This question is about relativistic kinematics.
A source of light S and a detector of light D are placed on opposite walls of a box as shown in the diagram.
According to an observer in the box the distance L between S and D is 6.0m. The box moves with speed v= 0.80c relative to the ground.
Consider the following events.
Event 1: a photon is emitted by S towards D
Event 2: the photon arrives at D
In the context of the theory of relativity, state what is meant by an event.
(i) Calculate the time interval t between event 1 and event 2 according to an observer in the box.
(ii) According to an observer on the ground the time interval between event 1 and event 2 is T. One student claims that \(T = \frac{t}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\) and another that \(T = t\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} \).
Explain why both students are wrong.
Relative to an observer on the ground,
(i) calculate the distance between S and D.
(ii) state the speed of the photon leaving S.
(iii) state an expression for the distance travelled by detector D in the time interval T (T is the interval in (b)(ii)).
(iv) determine T, using your answers to (c)(i), (ii) and (iii).
This question is about length contraction and simultaneity.
Define proper length.
A spaceship is travelling to the right at speed 0.75 c, through a tunnel which is open at both ends. Observer A is standing at the centre of one side of the tunnel. Observer A, for whom the tunnel is at rest, measures the length of the tunnel to be 240 m and the length of the spaceship to be 200 m. The diagram below shows this situation from the perspective of observer A.
Observer B, for whom the spaceship is stationary, is standing at the centre of the spaceship.
(i) Calculate the Lorentz factor, γ, for this situation.
(ii) Calculate the length of the tunnel according to observer B.
(iii) Calculate the length of the spaceship according to observer B.
(iv) According to observer A, the spaceship is completely inside the tunnel for a short time. State and explain whether or not, according to observer B, the spaceship is ever completely inside the tunnel.
Two sources of light are located at each end of the tunnel. The diagram below shows this situation from the perspective of observer A.
According to observer A, at the instant when observer B passes observer A, the two sources of light emit a flash. Observer A sees the two flashes simultaneously. Discuss whether or not observer B sees the two flashes simultaneously.
A spaceship S leaves the Earth with a speed v = 0.80c. The spacetime diagram for the Earth is shown. A clock on the Earth and a clock on the spaceship are synchronized at the origin of the spacetime diagram.
Calculate the angle between the worldline of S and the worldline of the Earth.
Draw, on the diagram, the x′-axis for the reference frame of S.
An event Z is shown on the diagram. Label the co-ordinates of this event in the reference frame of S.
An observer on Earth watches rocket A travel away from Earth at a speed of 0.80c. The spacetime diagram shows the worldline of rocket A in the frame of reference of the Earth observer who is at rest at x = 0.
Another rocket, B, departs from the same location as A but later than A at ct = 1.2 km according to the Earth observer. Rocket B travels at a constant speed of 0.60c in the opposite direction to A according to the Earth observer.
Rocket A and rocket B both emit a flash of light that are received simultaneously by the Earth observer. Rocket A emits the flash of light at a time coordinate ct = 1.8 km according to the Earth observer.
Draw on the spacetime diagram the worldline of B according to the Earth observer and label it B.
Deduce, showing your working on the spacetime diagram, the value of ct according to the Earth observer at which the rocket B emitted its flash of light.
Explain whether or not the arrival times of the two flashes in the Earth frame are simultaneous events in the frame of rocket A.
Calculate the velocity of rocket B relative to rocket A.
A rocket of proper length 450 m is approaching a space station whose proper length is 9.0 km. The speed of the rocket relative to the space station is 0.80c.
X is an observer at rest in the space station.
Two lamps at opposite ends of the space station turn on at the same time according to X. Using a Lorentz transformation, determine, according to an observer at rest in the rocket,
The rocket carries a different lamp. Event 1 is the flash of the rocket’s lamp occurring at the origin of both reference frames. Event 2 is the flash of the rocket’s lamp at time ct' = 1.0 m according to the rocket. The coordinates for event 2 for observers in the space station are x and ct.
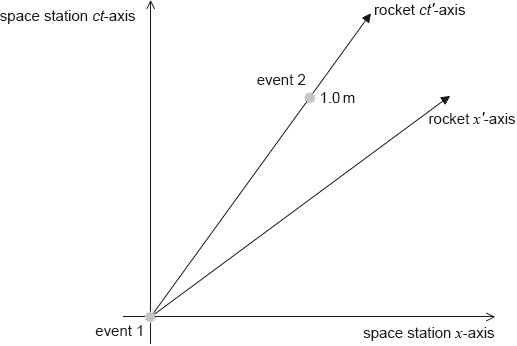
Calculate the length of the rocket according to X.
A space shuttle is released from the rocket. The shuttle moves with speed 0.20c to the right according to X. Calculate the velocity of the shuttle relative to the rocket.
the time interval between the lamps turning on.
which lamp turns on first.
On the diagram label the coordinates x and ct.
State and explain whether the ct coordinate in (c)(i) is less than, equal to or greater than 1.0 m.
Calculate the value of c 2t 2 – x 2.
An electron X is moving parallel to a current-carrying wire. The positive ions and the wire are fixed in the reference frame of the laboratory. The drift speed of the free electrons in the wire is the same as the speed of the external electron X.
Define frame of reference.
In the reference frame of the laboratory the force on X is magnetic.
(i) State the nature of the force acting on X in this reference frame where X is at rest.
(ii) Explain how this force arises.
This question is about special relativity, simultaneity and length contraction.
One of the two postulates of special relativity may be stated as:
“The laws of physics are the same for all observers in inertial reference frames.”
State
(i) what is meant by an inertial frame of reference.
(ii) the other postulate of special relativity.
In a thought experiment to illustrate the concept of simultaneity, Vladimir is standing on the ground close to a straight, level railway track. Natasha is in a railway carriage that is travelling along the railway track with constant speed v in the direction shown.
Natasha is sitting on a chair that is equidistant from each end of the carriage. At either end of the carriage are two clocks C1 and C2. Next to Natasha is a switch that, when operated, sends a signal to each clock. The clocks register the time of arrival of the signals. At the instant that Natasha and Vladimir are opposite each other, Natasha operates the switch. According to Natasha, C1 and C2 register the same time of arrival of each signal.
Explain, according to Vladimir, whether or not C1 and C2 register the same time of arrival for each signal.
The speed v of the carriage is 0.70c. Vladimir measures the length of the table at which Natasha is sitting to be 1.0 m.
(i) Calculate the length of the table as measured by Natasha.
(ii) Explain which observer measures the proper length of the table.
When a spaceship passes the Earth, an observer on the Earth and an observer on the spaceship both start clocks. The initial time on both clocks is 12 midnight. The spaceship is travelling at a constant velocity with γ = 1.25. A space station is stationary relative to the Earth and carries clocks that also read Earth time.
Some of the radio signal is reflected at the surface of the Earth and this reflected signal is later detected at the spaceship. The detection of this signal is event B. The spacetime diagram is shown for the Earth, showing the space station and the spaceship. Both axes are drawn to the same scale.
Calculate the velocity of the spaceship relative to the Earth.
The spaceship passes the space station 90 minutes later as measured by the spaceship clock. Determine, for the reference frame of the Earth, the distance between the Earth and the space station.
As the spaceship passes the space station, the space station sends a radio signal back to the Earth. The reception of this signal at the Earth is event A. Determine the time on the Earth clock when event A occurs.
Construct event A and event B on the spacetime diagram.
Estimate, using the spacetime diagram, the time at which event B occurs for the spaceship.
This question is about relativistic kinematics.
State what is meant by an inertial frame of reference.
A spaceship travels from space station Alpha to space station Zebra at a constant speed of 0.90c relative to the space stations. The distance from Alpha to Zebra is 10ly according to space station observers. At this speed γ=2.3.
Calculate the time taken to travel between Alpha and Zebra in the frame of reference of an observer
(i) on the Alpha space station.
(ii) on the spaceship.
Explain which of the time measurements in (b)(i) and (b)(ii) is a proper time interval.
The spaceship arrives at Zebra and enters an airlock at constant speed. O is an observer at rest relative to the airlock. Two lamps P and Q emit a flash simultaneously according to the observer S in the spaceship. At that instant, O and S are opposite each other and midway between the lamps.
Discuss whether the lamps flash simultaneously according to observer O.
This question is about relativistic kinematics.
Speedy is in a spacecraft being chased by Police Officer Sylvester. In Officer Sylvester’s frame of reference, Speedy is moving directly towards Officer Sylvester at 0.25c.
Describe what is meant by a frame of reference.
At a later time the police spacecraft is alongside Speedy’s spacecraft. The police spacecraft is overtaking Speedy’s spacecraft at a constant velocity.
Officer Sylvester is at a point midway between the flashing lamps, both of which he can see. At the instant when Officer Sylvester and Speedy are opposite each other, Speedy observes that the blue lamps flash simultaneously.
State and explain which lamp is observed to flash first by Officer Sylvester.
The police spacecraft is travelling at a constant speed of 0.5c relative to Speedy’s frame of reference. The light from a flash of one of the lamps travels across the police spacecraft and is reflected back to the light source. Officer Sylvester measures the time taken for
the light to return to the source as 1.2 × 10–8s.
(i) Outline why the time interval measured by Officer Sylvester is a proper time interval.
(ii) Determine, as observed by Speedy, the time taken for the light to travel across the police spacecraft and back to its source.
This question is about relativistic kinematics.
A spacecraft leaves Earth and moves towards a planet. The spacecraft moves at a speed 0.60c relative to the Earth. The planet is a distance of 12ly away according to the observer on Earth.
Determine the time, in years, that it takes the spacecraft to reach the planet according to the
(i) observer on Earth.
(ii) observer in the spacecraft.
The spacecraft passes a space station that is at rest relative to the Earth. The proper length of the space station is 310 m.
(i) State what is meant by proper length.
(ii) Calculate the length of the space station according to the observer in the spacecraft.
F and B are two flashing lights located at the ends of the space station, as shown. As the spacecraft approaches the space station in (b), F and B turn on. The lights turn on simultaneously according to the observer on the space station who is midway between the lights.
State and explain which light, F or B, turns on first according to the observer in the spacecraft.
This question is about relativistic kinematics.
In a thought experiment, a train is moving at a speed of 0.950c relative to the ground. A pendulum attached to the ceiling of the train is set into oscillation.
An observer T on the train and an observer G on the ground measure the period of oscillation of the pendulum.
State and explain whether the pendulum period is a proper time interval for observer T, observer G or both T and G.
Observer T measures the period of oscillations of the pendulum to be 0.850s. Calculate the period of oscillations according to observer G.
Observer T is standing in the middle of a train watched by observer G at the side of the track. Two lightning strikes hit the ends of
the train. The strikes are simultaneous according to observer T.
Light from the strikes reaches both observers.
(i) Explain why, according to observer G, light from the two strikes reaches observer T at the same time.
(ii) Using your answer to (i), explain why, according to observer G, end X of the train was hit by lightning first.
An observer P sitting in a train moving at a speed v measures that his journey takes a time ΔtP. An observer Q at rest with respect to the ground measures that the journey takes a time ΔtQ.
According to Q there is an instant at which the train is completely within the tunnel.
At that instant two lights at the front and the back of the train are turned on simultaneously according to Q.
The spacetime diagram according to observer Q shows event B (back light turns on) and event F (front light turns on).

State which of the two time intervals is a proper time.
Calculate the speed v of the train for the ratio \(\frac{{\Delta {t_{\text{P}}}}}{{\Delta {t_{\text{Q}}}}} = 0.30\).
Later the train is travelling at a speed of 0.60c. Observer P measures the length of the train to be 125 m. The train enters a tunnel of length 100 m according to observer Q.
Show that the length of the train according to observer Q is 100 m.
Draw the time \(ct'\) and space \(x'\) axes for observer P’s reference frame on the spacetime diagram.
Deduce, using the spacetime diagram, which light was turned on first according to observer P.
Apply a Lorentz transformation to show that the time difference between events B and F according to observer P is 2.5 × 10–7 s.
Demonstrate that the spacetime interval between events B and F is invariant.
A second train is moving at a velocity of –0.70c with respect to the ground.
Calculate the speed of the second train relative to observer P.
An observer on Earth watches a rocket A. The spacetime diagram shows part of the motion of A in the reference frame of the Earth observer. Three flashing light beacons, X, Y and Z, are used to guide rocket A. The flash events are shown on the spacetime diagram.
The diagram shows the axes for the reference frames of Earth and of rocket A. The Earth observer is at the origin.
For the reference frame of the Earth observer, calculate the speed of rocket A in terms of the speed of light c.
Using the graph opposite, deduce the order in which
(i) the beacons flash in the reference frame of rocket A.
(ii) the Earth observer sees the beacons flash.