Determine the standard enthalpy change, $∆H^{⦵}$, for this reaction, using section 11 of the data booklet.

Calculate the standard enthalpy change, $∆H^{⦵}$, for this reaction using section 12 of the data booklet.

Predict, giving a reason, whether the entropy change, $∆S^{⦵}$, for this reaction is negative or positive.

Calculate $∆S^{⦵}$ for the reaction in $\mathrm{J} {\mathrm{K}}^{-1}$, using section 12 of the data booklet.

The standard molar entropy for oxygen gas is $205 \mathrm{J} {\mathrm{K}}^{-1} {\mathrm{mol}}^{-1}$.

Calculate the standard Gibbs free energy change, $∆{\mathrm{G}}^{⦵}$, in $\mathbf{kJ}$, for the reaction at 5 °C, using your answers to (b) and (d). Use section 1 of the data booklet.

(If you did not obtain an answer to (b) or (d) use values of $-1952 \mathrm{kJ}$ and $+113 \mathrm{J} {\mathrm{K}}^{-1}$ respectively, although these are not the correct answers.)

Bonds broken: 8(C–H) + 2(C–C) + 5(O=O) / 8 × 414 «kJ mol⁻¹» + 2 × 346 «kJ mol⁻¹» + 5 × 498 «kJ mol−1» / 6494 «kJ» ✔

Bonds formed: 6(C=O) + 8(O–H) / 6 × 804 «kJ mol⁻¹» + 8 × 463 «kJ mol⁻¹» / 8528 «kJ» ✔

«Enthalpy change$=$bonds broken$-$bonds formed $=6494 \mathrm{kJ}-8528 \mathrm{kJ}=»-2034 «\mathrm{kJ}»$ ✔

Award [3] for correct final answer.

$4(-241.8 «\mathrm{kJ}»)$ AND $3(-393.5 «\mathrm{kJ}»)$ AND $«1»(-105 «\mathrm{kJ}»)$ ✔
$«\mathrm{\Delta }{H}^{⦵}=4(-241.8 «\mathrm{kJ}»)+3(-393.5 «\mathrm{kJ}»)–«1»(-105 «\mathrm{kJ}»)=»-2043 «\mathrm{kJ}»$ ✔

Award [2] for correct final answer.

Award [1 max] for $\mathit{-}\mathit{2219}\mathit{ }«kJ»$.

positive AND more moles «of gas» in products ✔

$4\times 188.8 «\mathrm{J} {\mathrm{K}}^{-1}»$ AND $3\times 213.8 «\mathrm{J} {\mathrm{K}}^{-1}»$ AND $«1\times »270 «\mathrm{J} {\mathrm{K}}^{-1}»$ AND $5\times 205 «\mathrm{J} {\mathrm{K}}^{-1}»$ ✔

$«∆S^{⦵}=4(188.8 \mathrm{J} {\mathrm{K}}^{-1})+3(213.8 \mathrm{J} {\mathrm{K}}^{-1})–\left[1\right(270 \mathrm{J} {\mathrm{K}}^{-1})+5(205 \mathrm{J} {\mathrm{K}}^{-1}\left)\right]=»102«\mathrm{J} {\mathrm{K}}^{-1}»$ ✔

Award [2] for correct final answer.

$«\mathrm{T}=5+273=»278 \mathrm{K}$ ✔

$«{\mathrm{\Delta G}}^{⦵}=-2043 \mathrm{kJ}-(278 \mathrm{K}\times 0.102 \mathrm{kJ} {\mathrm{K}}^{-1})=»-2071 «\mathrm{kJ}»$ ✔

Award [2] for correct final answer.

Many candidates had difficulty determining the number and type of bonds broken or formed and consequently this was the part of question 3 that was most poorly attempted. Those that could identify these bonds performed the calculations correctly.

Enthalpy calculations using enthalpy of formation data were generally well done.

Most knew that entropy increased however some lost the mark by not including an explanation based on increase number of mol of gaseous products.

Calculating ΔS^ө, like most other calculations, was well done.

ΔG^ө calculations were also well done, with some not seeing that specific units were to be used.

Formulate an equation for the oxidation of nickel(II) sulfide to nickel(II) oxide.

The nickel obtained from another ore, nickeliferous limonite, is contaminated with iron. Both nickel and iron react with carbon monoxide gas to form gaseous complexes, tetracarbonylnickel, $\text{Ni(CO}{\text{)}}_{\text{4}}\text{(g)}$, and pentacarbonyliron, $\text{Fe(CO}{\text{)}}_{\text{5}}\text{(g)}$. Suggest why the nickel can be separated from the iron successfully using carbon monoxide.

Calculate the standard entropy change, $\mathrm{\Delta }{S}^{\theta }$, of the reaction, in $\text{J}{\text{K}}^{-1}$, using the values given.

Calculate a value for $\mathrm{\Delta }{H}^{\theta }$ in kJ.

Use your answers to (c)(i) and (c)(ii), to determine the temperature, in °C, at which the decomposition of liquid tetracarbonylnickel to nickel and carbon monoxide becomes favourable.

(If you did not get answers to (c)(i) and (c)(ii), use $-500\text{ J}{\text{K}}^{-1}$ and $-200\text{ kJ}$ respectively but these are not the correct answers.)

Suggest why experiments involving tetracarbonylnickel are very hazardous.

$\text{2NiS(s)}+\text{3}{\text{O}}_{\text{2}}\text{(g)}\to \text{2NiO(s)}+\text{2S}{\text{O}}_{\text{2}}\text{(g)}$

[1 mark]

formation of «gaseous» pentacarbonyliron is slower
OR
«gaseous» complexes form at different rates
OR
gases have different rates of diffusion «due to difference in masses»
OR
difference in thermal stability of «gaseous» complexes
OR
difference in boiling points of «gaseous» complexes
OR
difference in solubility of «gaseous» complexes
OR
difference in surface affinity «onto solid absorbent»
OR
difference in chemical properties of «gaseous» complexes

Accept any other valid answer.

[1 mark]

$\sum S_{\text{RHS}}^{\theta }=313.4\ll \text{J}{\text{K}}^{-1}\gg$
AND
$\sum S_{\text{LHS}}^{\theta }=\ll (4\times 197.6)+29.9\text{ J}{\text{K}}^{-1}=\gg 820.3\ll \text{J}{\text{K}}^{-1}\gg$

$\mathrm{\Delta }{S}^{\theta }\ll =\sum S_{\text{RHS}}^{\theta }-\sum S_{\text{LHS}}^{\theta }=313.4-820.3\gg =-506.9\ll \text{J}{\text{K}}^{-1}\gg$

Award [2] for correct final answer.

[2 marks]

$\mathrm{\Delta }{H}^{\theta }\ll =-633.0-4\times (-110.5)\gg =-191\ll kJ\gg$

[1 mark]

«when» $\mathrm{\Delta }G=0$ «forward and backward reactions are equally favourable»

«when $\mathrm{\Delta }G=0$, $\text{T}=\frac{\mathrm{\Delta }H}{\mathrm{\Delta }S}$», $\text{T}=\ll \frac{191\text{ kJ}}{0.5069\text{ kJ}{\text{K}}^{-1}}=\gg 377\ll \text{K}\gg$

«temperature =» 104 «°C»

Award [3] for correct final answer. Use of –500 J K^–1 and –200 kJ gives 127 °C.

Award [2 max] for T < 104 «°C».

Accept ΔG < 0 and T > 104 «°C».

[3 marks]

CO is toxic/poisonous
OR
Ni(CO)₄ decomposition deposits nickel in the lungs
OR
tetracarbonylnickel is toxic/poisonous
OR
tetracarbonylnickel is highly flammable «auto-ignition temperature of 60 °C»

[1 mark]

Predict the electron domain and molecular geometries around the oxygen atom of molecule A using VSEPR

State the type of hybridization shown by the central carbon atom in molecule B.

State the number of sigma ($\mathrm{\sigma }$) and pi ($\mathrm{\pi }$) bonds around the central carbon atom in molecule B.

The IR spectrum of one of the compounds is shown:

COBLENTZ SOCIETY. Collection © 2018 copyright by the U.S. Secretary of Commerce on behalf of the United States of America. All rights reserved.

Deduce, giving a reason, the compound producing this spectrum.

Compound A and B are isomers. Draw two other structural isomers with the formula ${\mathrm{C}}_3{\mathrm{H}}_6\mathrm{O}$.

The equilibrium constant, $K_{\mathrm{c}}$, for the conversion of A to B is $1.0\times {10}^8$ in water at $298 \mathrm{K}$.

Deduce, giving a reason, which compound, A or B, is present in greater concentration when equilibrium is reached.

Calculate the standard Gibbs free energy change, $∆G^{⦵}$, in $\mathbf{kJ}\mathbf{ }{\mathbf{mol}}^{\mathbf{–}\mathbf{1}}$, for the reaction (A to B) at $298 \mathrm{K}$. Use sections 1 and 2 of the data booklet.

Propanone can be synthesized in two steps from propene. Suggest the synthetic route including all the necessary reactants and steps.

Propanone can be synthesized in two steps from propene.

Suggest why propanal is a minor product obtained from the synthetic route in (g)(i).

Electron domain geometry: tetrahedral ✔

Molecular geometry: bent/V-shaped ✔

${\mathrm{sp}}^2$ ✔

$\mathrm{\sigma }$-bonds: $3$
AND
$\mathrm{\pi }$-bonds: $1$ ✔

B AND $\mathrm{C}=\mathrm{O}$ absorption/$1750«{\mathrm{cm}}^{-1}»$ 
OR
B AND absence of $\mathrm{O}–\mathrm{H} /3200-3600«{\mathrm{cm}}^{-1} \mathrm{absorption}»$✔

Accept any value between $\mathit{1700}\mathit{-}\mathit{1750}\mathit{ }c{m}^{\mathit{-}\mathit{1}}$.

Accept any two $C_3{H}_{6}O$ isomers except for propanone and propen-2-ol:

✔✔

Penalize missing hydrogens in displayed structural formulas once only.

$\mathrm{B}$ AND $K_{\mathrm{c}}$ is greater than $1$/large ✔

$«\mathrm{\Delta }{G}^{\mathrm{\Theta }}=-RT\ln K=0.00831 \mathrm{kJ} {\mathrm{mol}}^{-1} {\mathrm{K}}^{-1} (298 \mathrm{K}) (\ln 1.0\times {10}^8)=»$
$-46«\mathrm{kJ} {\mathrm{mol}}^{-1}»$ ✔

${\mathrm{H}}_2\mathrm{O}$/water «and ${\mathrm{H}}^{+}$» ✔

${\mathrm{CH}}_3\mathrm{CH}\left(\mathrm{OH}\right){\mathrm{CH}}_3$/propan-2-ol ✔

${\mathrm{K}}_2{\mathrm{Cr}}_2{\mathrm{O}}_7$/«potassium» dichromate(VI) AND ${\mathrm{H}}^{+}$
OR
${\mathrm{KMnO}}_4$/«acidified potassium» manganate(VII) ✔

Accept $H_{\mathit{3}}{O}^{\mathit{+}}$.

primary carbocation «intermediate forms»
OR
minor product «of the water addition would be» propan-1-ol
OR
anti-Markovnikov addition of water ✔

primary alcohol/propan-1-ol oxidizes to an aldehyde/propanal ✔

The majority of students got at least one of electron domain geometry or molecular geometry correct.

The vast majority of students could identify the hybridization around a central carbon atom.

The vast majority of students could identify BOTH sigma and pi bonds in a molecule.

Many candidates identified B having C = O and a peak at 1750.

A surprising number of candidates drew propanone here as an option, either failing to read the question or perhaps finding the structural formulae provided difficult to understand.

Most candidates identified B, the product, as being in greater concentration at equilibrium however some lost the mark because they did not include a reason.

Most candidates could apply the formula for Gibbs free energy change, ΔG^Θ, correctly however some did not get the units correct.

The mean mark was ⅔ for the required synthetic route. Some candidates failed to identify water as a reagent in the hydration reaction, or note that dichromate ion oxidation requires acidic conditions. This was also the question with most No Response.

This question regarding the formation of a minor product was not well answered. Many candidates struggled to explain the formation of propan-1-ol and to then oxidize it to propanal.

Hydrogenation of propene produces propane. Calculate the standard entropy change, ΔS^θ, for the hydrogenation of propene.

The standard enthalpy change, ΔH ^θ, for the hydrogenation of propene is –124.4 kJ mol^–1. Predict the temperature above which the hydrogenation reaction is not spontaneous.

«ΔS^θ =» 270 «J K^–1 mol^–1» – 267 «J K^–1 mol^–1» – 131 «J K^–1 mol^–1»

«ΔS^θ =» –128 «J K^–1 mol^–1»

Award [2] for correct final answer.

[2 marks]

«non spontaneous if» ΔG ^θ = ΔH ^θ – TΔS ^θ > 0
OR
ΔH ^θ > TΔS ^θ

«T above» $\frac{-124.4\ll \text{kJ}\text{mo}{\text{l}}^{-\text{1}}\gg }{-0.128\ll \text{kJ}{\text{K}}^{-1}\text{mo}{\text{l}}^{-\text{1}}\gg }=$» 972 «K»

Award [2] for correct final answer.

Accept 699 °C.

Do not award M2 for any negative T value.

[2 marks]

Determine the oxidation state of vanadium in each of the following species.

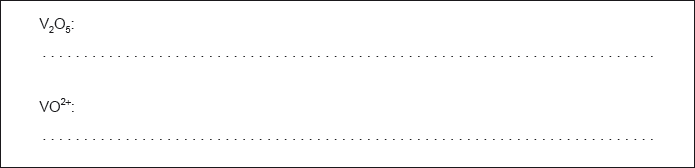
Identify, from the table, a non-vanadium species that can reduce VO²⁺(aq) to V³⁺(aq) but no further.

Identify, from the table, a non-vanadium species that could convert ${\text{VO}}_2^{+}\text{(aq)}$ to V²⁺(aq).

Formulate an equation for the reaction between VO²⁺(aq) and V²⁺(aq) in acidic solution to form V³⁺(aq).

Comment on the spontaneity of this reaction by calculating a value for $\mathrm{\Delta }{G}^{\theta }$ using the data given in (b) and in section 1 of the data booklet.

$V_2{O}_5:+5$
$V{O}^{2+}:+4$

Do not penalize incorrect notation twice.

[2 marks]

H₂SO₃(aq)
OR
Pb(s)

[1 mark]

Zn(s)

[1 mark]

$\text{V}{\text{O}}^{2+}(\text{aq)}+{\text{V}}^{2+}(\text{aq)}+\text{2}{\text{H}}^{+}(\text{aq)}\to \text{2}{\text{V}}^{3+}(\text{aq)}+{\text{H}}_{\text{2}}\text{O(l)}$

Accept equilibrium sign.

[1 mark]

$E^{\theta }\ll =+0.34\text{ V}-(-0.26\text{ V})\gg =+0.60\ll \text{V}\gg$

$\mathrm{\Delta }{G}^{\theta }=\ll -nF{E}^{\theta }=-9.65\times {10}^4\text{ C}\text{mo}{\text{l}}^{-1}\times 0.60\text{ J}{\text{C}}^{-1}=\gg -57900\ll \text{J}\text{mo}{\text{l}}^{-1}\gg /-57.9\ll \text{kJ}\text{mo}{\text{l}}^{-1}\gg$

spontaneous as $\mathrm{\Delta }{G}^{\theta }$ is negative

Do not award M3 as a stand-alone answer.

Accept “spontaneous” for M3 if answer given for M2 is negative.

Accept “spontaneous as $E^{\theta }$ is positive” for M3.

[3 marks]

Calculate the standard enthalpy change for this reaction using the following data.

Calculate the standard entropy change for this reaction using the following data.

The standard free energy change, ΔG^θ, for the above reaction is –103 kJ mol^–1 at 298 K.

Suggest why ΔG^θ has a large negative value considering the sign of ΔH^θ in part (a).

ΔH^θ = [–165.2 + 2(–296.9) + 2(–92.3)] – [–454.7 + 2(–245.7)]

«ΔH^θ = +»2.5 «kJ»

Award [2] for correct final answer.

Award [1] for –2.5 «kJ».

Do not accept ECF for M2 if more than one error in M1.

«ΔS^θ = [208.5 + 2(248.1) + 2(186.8)] – [166.9 + 2(278.6)]»

«ΔS^θ = +» 354.2 «J K^–1 mol^–1»

«3 moles of» liquid to «4 moles of» gas

OR

«large» positive ΔS

OR

«large» increase in entropy

TΔS > ΔH «at the reaction temperature»

Ethyne, like ethene, undergoes hydrogenation to form ethane. State the conditions required.

Outline the formation of polyethene from ethene by drawing three repeating units of the polymer.

Ethyne reacts with chlorine in a similar way to ethene. Formulate equations for the following reactions.

Under certain conditions, ethyne can be converted to benzene.

Determine the standard enthalpy change, ΔH^Θ, for the reaction stated, using section 11 of the data booklet.

3C₂H₂(g) → C₆H₆(g)

Determine the standard enthalpy change, ΔH^Θ, for the following similar reaction, using ΔH_f values in section 12 of the data booklet.

3C₂H₂(g) → C₆H₆(l)

Explain, giving two reasons, the difference in the values for (c)(i) and (ii). If you did not obtain answers, use −475 kJ for (i) and −600 kJ for (ii).

Calculate the standard entropy change, ΔS^Θ, in J K⁻¹, for the reaction in (ii) using section 12 of the data booklet.

Determine, showing your working, the spontaneity of the reaction in (ii) at 25 °C.

One possible Lewis structure for benzene is shown.

State one piece of physical evidence that this structure is incorrect.

nickel/Ni «catalyst»

high pressure

OR

heat

Accept these other catalysts: Pt, Pd, Ir, Rh, Co, Ti.

Accept “high temperature” or a stated temperature such as “150 °C”.

[2 marks]

Ignore square brackets and “n”.

Connecting line at end of carbons must be shown.

[1 mark]

ethyne: C₂H₂ + Cl₂ → CHClCHCl

benzene: C₆H₆ + Cl₂ → C₆H₅Cl + HCl

Accept “C₂H₂Cl₂”.

[2 marks]

ΔH^Θ = bonds broken – bonds formed

«ΔH^Θ = 3(C≡C) – 6(CC)_benzene / 3 $\times$ 839 – 6 $\times$ 507 / 2517 – 3042 =» –525 «kJ»

Award [2] for correct final answer.

Award [1 max] for “+525 «kJ»”.

Award [1 max] for:

«ΔH^Θ = 3(C≡C) – 3(C–C) – 3(C=C) / 3 $\times$ 839 – 3 $\times$ 346 – 3 $\times$ 614 / 2517 – 2880 =» –363 «kJ».

[2 marks]

ΔH^Θ = ΣΔH_f (products) – ΣΔH_f (reactants)

«ΔH^Θ = 49 kJ – 3 $\times$ 228 kJ =» –635 «kJ»

Award [2] for correct final answer.

Award [1 max] for “+635 «kJ»”.

[2 marks]

ΔH_f values are specific to the compound

OR

bond enthalpy values are averages «from many different compounds»

condensation from gas to liquid is exothermic

Accept “benzene is in two different states «one liquid the other gas»” for M2.

[2 marks]

«ΔS^Θ = 173 – 3 $\times$ 201 =» –430 «J K^–1»

[1 mark]

T = «25 + 273 =» 298 «K»

ΔG^ϴ «= –635 kJ – 298 K × (–0.430 kJ K^–1)» = –507 kJ

ΔG^ϴ < 0 AND spontaneous

ΔG^ϴ < 0 may be inferred from the calculation.

[3 marks]

equal C–C bond «lengths/strengths»

OR

regular hexagon

OR

«all» C–C have bond order of 1.5

OR

«all» C–C intermediate between single and double bonds

Accept “all C–C–C bond angles are equal”.

[1 mark]

Hydrogen gas can be formed industrially by the reaction of natural gas with steam.

                                          CH₄(g) + H₂O(g) → 3H₂(g) + CO(g)

Determine the enthalpy change, ΔH, for the reaction, in kJ, using section 11 of the data booklet.

Bond enthalpy for C≡O: 1077 kJ mol⁻¹

Outline why no value is listed for H₂(g).

Determine the value of ΔH^Θ, in kJ, for the reaction using the values in the table.

The table lists standard entropy, S^Θ, values.

Calculate the standard entropy change for the reaction, ΔS^Θ, in J K⁻¹.

CH₄(g) + H₂O(g) → 3H₂(g) + CO(g)

Calculate the standard free energy change, ΔG^Θ, in kJ, for the reaction at 298 K using your answer to (b)(ii).

Determine the temperature, in K, above which the reaction becomes spontaneous.

bonds broken: 4(C–H) + 2(H–O)/4(414) + 2(463)/2582 «kJ»

bonds made: 3(H–H) + C≡O/3(436) + 1077/2385 «kJ»

ΔH «= ΣBE_{(bonds broken)} – ΣBE_{(bonds made)} = 2582 – 2385» = «+» 197 «kJ»

Award [3] for correct final answer.

Award [2 max] for –197 «kJ».

[3 marks]

$\mathrm{\Delta }{H}_{\text{f}}^{\mathrm{\Theta }}$ for any element = 0 «by definition»

OR

no energy required to form an element «in its stable form» from itself

[1 mark]

ΔH^Θ « = $\sum \mathrm{\Delta }{H}_{\text{f}}^{\mathrm{\Theta }}$_(products) – $\sum \mathrm{\Delta }{H}_{\text{f}}^{\mathrm{\Theta }}$_(reactants) = –111 + 0 – [–74.0 + (–242)]»

= «+» 205 «kJ»

[1 mark]

«ΔS^Θ = ΣS^Θ_products – ΣS^Θ_reactants = 198 + 3 × 131 – (186 + 189) =» «+» 216 «J K^–1»

[1 mark]

«ΔG^Θ = ΔH^Θ – TΔS^Θ = 205 kJ – 298 K × $\frac{216}{1000}$ kJ K^–1 =» «+» 141 «kJ»

[1 mark]

«ΔH^Θ = TΔS^Θ»

«$\text{T}=\frac{\mathrm{\Delta }{H}^{\mathrm{\Theta }}}{\mathrm{\Delta }{S}^{\mathrm{\Theta }}}=\frac{205000\text{ J}}{216\text{ J }{\text{K}}^{-1}}$»

«T =» 949 «K»

Do not award a mark for negative value of T.

[1 mark]

Deduce the order of reaction with respect to hydrogen.

Deduce the rate expression for the reaction.

Calculate the value of the rate constant stating its units.

State two conditions necessary for a successful collision between reactants.

State the equilibrium constant expression, K_c, for this reaction.

Calculate the entropy change of reaction, ΔS^⦵, in J K⁻¹ mol⁻¹.

Predict, giving a reason, how the value of the ΔS^⦵_reaction would be affected if ${\text{I}}_2$ (g) were used as a reactant.

Calculate the Gibbs free energy change, ΔG^⦵, in kJ mol⁻¹, for the reaction at 298 K. Use section 1 of the data booklet.

Calculate the equilibrium constant, K_c, for this reaction at 298 K. Use your answer to (d)(iii) and sections 1 and 2 of the data booklet.

(If you did not obtain an answer to (d)(iii) use a value of 2.0 kJ mol⁻¹, although this is not the correct answer).

first order ✔

Rate=k [H₂] [$\text{I}$₂]

$k=«\frac{1.2\times {10}^{-6} \mathrm{mol} {\mathrm{dm}}^{-3} {\mathrm{s}}^{-1}}{2.0\times {10}^{-3} \mathrm{mol} {\mathrm{dm}}^{-3}\times 3.0\times {10}^{-3} \mathrm{mol} {\mathrm{dm}}^{-3}}=»0.20$ ✔

mol^–1 dm³ s^–1 ✔

E ≥ E_a AND appropriate «collision» geometry/correct orientation ✔

$K_{\mathrm{c}}=\frac{{\left[\mathrm{HI}\right]}^2}{\left[{\mathrm{H}}_2\right]\left[{\mathrm{I}}_2\right]}$ ✔

«Δ${S^{⦵}}_{\text{reaction}}$ = 2 × 206.6 – (130.6 + 116.1) =» 166.5 «J K^–1 mol^–1» ✔

Δ${S^{⦵}}_{\text{reaction}}$ lower/less positive AND same number of moles of gas

OR

Δ${S^{⦵}}_{\text{reaction}}$ lower/less positive AND a solid has less entropy than a gas ✔

«ΔG^⦵ = 53.0 kJ mol^–1 – (298K × 0.1665 kJ K^–1 mol^–1) =» 3.4 «kJ mol^–1» ✔

«ln K_c= – (3.4 × 10³ J mol^–1 /8.31 J K^–1 mol^–1 × 298 K)» = –1.37 ✔

«K_c =» 0.25 ✔

Award [2] for “0.45” for the use of 2.0 kJ mol^–1 for ΔG^⦵.

4(a)(i)-(iii): Deduction of rate orders and rate expression were very well done overall, with occasional errors in the units of the rate constant, but clearly among the best answered questions.

Generally well answered by all but very weak candidates. Some teachers thought this should be a 2-mark question but actually the marks were generally missed when students mentioned both required conditions but failed to refer the necessary energy to E_a.

One of the best answered questions.

ΔS was well calculated in general except for some inverted calculations or failure to consider the ratios of the reactants.

Some candidates confused the entropy change in this situation with absolute entropy of a solid and gas, or having realised that entropy would decrease lacked clarity in their explanations and lost the mark.

4(d)(ii)-(d)(iv): marks were lost due to inconsistency of units throughout, i.e., not because answers were given in different units to those required, but because candidates failed to convert all data to the same unit for calculations.

Calcium carbonate is heated to produce calcium oxide, CaO.

CaCO₃(s) → CaO (s) + CO₂(g)

Calculate the volume of carbon dioxide produced at STP when 555 g of calcium carbonate decomposes. Use sections 2 and 6 of the data booklet.

Calculate the enthalpy change of reaction, ΔH, in kJ, for the decomposition of calcium carbonate.

Calculate the change in entropy, ΔS, in J K⁻¹, for the decomposition of calcium carbonate.

Determine the temperature, in K, at which the decomposition of calcium carbonate becomes spontaneous, using b(i), b(ii) and section 1 of the data booklet.

(If you do not have answers for b(i) and b(ii), use ΔH = 190 kJ and ΔS = 180 J K⁻¹, but these are not the correct answers.)

Sketch an energy profile for the decomposition of calcium carbonate based on your answer to b(i), labelling the axes and activation energy, E_a.

State how adding a catalyst to the reaction would impact the enthalpy change of reaction, ΔH, and the activation energy, E_a.

Write the equation for the reaction of Ca(OH)₂(aq) with hydrochloric acid, HCl (aq).

Determine the volume, in dm³, of 0.015 mol dm⁻³ calcium hydroxide solution needed to neutralize 35.0 cm³ of 0.025 mol dm⁻³ HCl (aq).

Saturated calcium hydroxide solution is used to test for carbon dioxide. Calculate the pH of a 2.33 × 10⁻²mol dm⁻³ solution of calcium hydroxide, a strong base.

Determine the mass, in g, of CaCO₃(s) produced by reacting 2.41 dm³ of 2.33 × 10⁻² mol dm⁻³ of Ca(OH)₂ (aq) with 0.750 dm³ of CO₂ (g) at STP.

2.85 g of CaCO₃ was collected in the experiment in d(i). Calculate the percentage yield of CaCO₃.

(If you did not obtain an answer to d(i), use 4.00 g, but this is not the correct value.)

Outline how one calcium compound in the lime cycle can reduce a problem caused by acid deposition.

«n_CaCO3 = $\frac{555 \mathrm{g}}{11.09 \mathrm{g} {\mathrm{mol}}^{-1}}$=» 5.55 «mol» ✓

«V = 5.55 mol × 22.7 dm³ mol⁻¹ =» 126 «dm³» ✓

Award [2] for correct final answer.

Accept method using pV = nRT to obtain the volume with p as either 100 kPa (126 dm³) or 101.3 kPa (125 dm³).

Do not penalize use of 22.4 dm³ mol^–1 to obtain the volume (124 dm³).

«ΔH =» (−635 «kJ» – 393.5 «kJ») – (−1207 «kJ») ✓

«ΔH = + » 179 «kJ» ✓

Award [2] for correct final answer.

Award [1 max] for −179 kJ.

Ignore an extra step to determine total enthalpy change in kJ: 179 kJ mol^-1 x 5.55 mol = 993 kJ.

Award [2] for an answer in the range 990 - 993« kJ».

«ΔS = (40 J K⁻¹ + 214 J K⁻¹) − (93 J K⁻¹) =» 161 «J K⁻¹» ✓

Ignore an extra step to determine total entropy change in JK^–1: 161 J mol^–1K^–1 x 5.55 mol = 894 «J mol^–1K^–1»

Award [1] for 894 «J mol^–1K^–1».

«spontaneous» if ΔG = ΔH − TΔS < 0
OR
ΔH < TΔS ✓

«T >$\frac{179 \mathrm{kJ}}{0.16 \mathrm{kJ} {\mathrm{K}}^{-1}}$=» 1112 «K» ✓

Award [2] for correct final answer.

Accept “1056 K” if both of the incorrect values are used to solve the problem.

Do not award M2 for any negative T value.

endothermic sketch ✓

x-axis labelled “extent of reaction/progress of reaction/reaction coordinate/reaction pathway” AND y-axis labelled “potential energy/energy/enthalpy✓

activation energy/E_a ✓

Do not accept “time” for x-axis.

ΔH same AND lower E_a ✓

Ca(OH)₂(aq) + 2HCl (aq) → 2H₂O (l) + CaCl₂(aq) ✓

«n_HCl = 0.0350 dm³ × 0.025 mol dm⁻³ =» 0.00088 «mol»

OR
n_Ca(OH)2 = $\frac{1}{2}$ n_HCl/0.00044 «mol» ✓

«V = $\frac{{\displaystyle \frac{1}{2}\times 0.00088 \mathrm{mol}}}{0.015 \mathrm{mol} {\mathrm{dm}}^{-3}}$ =» 0.029 «dm³» ✓

Award [2] for correct final answer.

Award [1 max] for 0.058 «dm³».

Alternative 1:

[OH⁻] = « 2 × 2.33 × 10⁻²mol dm⁻³ =» 0.0466 «mol dm⁻³» ✓

«[H⁺] = $\frac{1.00\times {10}^{-14}}{0.0466}$ = 2.15 × 10⁻¹³mol dm⁻³»

pH = « −log (2.15 × 10−13) =» 12.668 ✓

Alternative 2:

[OH⁻] =« 2 × 2.33 × 10⁻² mol dm⁻³ =» 0.0466 «mol dm⁻³» ✓

«pOH = −log (0.0466) = 1.332»

pH = «14.000 – pOH = 14.000 – 1.332 =» 12.668 ✓

Award [2] for correct final answer.

Award [1 max] for pH =12.367.

«n_Ca(OH)2 = 2.41 dm³ × 2.33 × 10⁻²mol dm⁻³ =» 0.0562 «mol» AND

«n_CO2 =$\frac{0.750 {\mathrm{dm}}^3}{22.7 \mathrm{mol} {\mathrm{dm}}^{-3}}$=» 0.0330 «mol» ✓

«CO₂ is the limiting reactant»

«m_CaCO3 = 0.0330 mol × 100.09 g mol⁻¹ =» 3.30 «g» ✓

Only award ECF for M2 if limiting reagent is used.

Accept answers in the range 3.30 - 3.35 «g».

«$\frac{2.85}{3.30}$ × 100 =» 86.4 «%» ✓

Accept answers in the range 86.1-86.4 «%».

Accept “71.3 %” for using the incorrect given value of 4.00 g.

«add» Ca(OH)₂/CaCO₃/CaO AND to «acidic» water/river/lake/soil
OR
«use» Ca(OH)₂/CaCO₃/CaO in scrubbers «to prevent release of acidic pollution» ✓

Accept any correct name for any of the calcium compounds listed.

Write the chemical equation for the complete combustion of ethanol.

Deduce the change in enthalpy, ΔH, in kJ, when 56.00 g of ethanol is burned. Use section 13 in the data booklet.

Oxidation of ethanol with potassium dichromate, K₂Cr₂O₇, can form two different organic products. Determine the names of the organic products and the methods used to isolate them.

Write the equation and name the organic product when ethanol reacts with methanoic acid.

Sketch the titration curve of methanoic acid with sodium hydroxide, showing how you would determine methanoic acid pK_a.

Identify an indicator that could be used for the titration in 5(d)(i), using section 22 of the data booklet.

Determine the concentration of methanoic acid in a solution of pH = 4.12. Use section 21 of the data booklet.

Identify if aqueous solutions of the following salts are acidic, basic, or neutral.

CH₃CH₂OH (l) + 3O₂(g) → 2CO₂(g) + 3H₂O (g) ✓

«n = $\frac{56.00 \mathrm{g}}{46.08 \mathrm{g} {\mathrm{mol}}^{-1}}$ =» 1.215 «mol» ✓

«1.215mol × (−1367 kJ mol⁻¹) =» −1661 «kJ» ✓

Award [2] for correct final answer.

Award [1 max] for “«+»1661 «kJ»”.

ethanal AND distillation ✓

ethanoic acid AND reflux «followed by distillation» ✓

Award [1] for both products OR both methods.

Equation:
CH₃CH₂OH + HCOOH $\rightleftharpoons$ HCOOCH₂CH₃ + H₂O ✓

Product name:
ethyl methanoate ✓

Accept equation without equilibrium arrows.

Accept equation with molecular formulas (C₂H₆O + CH₂O₂ $\rightleftharpoons$ C₃H₆O₂ + H₂O) only if product name is correct.

increasing S-shape pH curve ✓

pK_a: pH at half neutralization/equivalence ✓

M1: Titration curve must show buffer region at pH <7 and equivalence at pH >7.

Ignore other parts of the curve, i.e., before buffer region, etc.

Accept curve starting from where two axes meet as pH scale is not specified.

phenolphthalein
OR
phenol red ✓

Alternative 1:
K_a = $\frac{\left[{\mathrm{H}}^{+}\right]\left[{\mathrm{HCOO}}^{-}\right]}{\left[\mathrm{HCOOH}\right]}$
OR
[HCOOH] = $\frac{{\left({10}^{-4.12}\right)}^2}{{10}^{-3.75}}$✓

«[HCOOH] =» 3.24 × 10⁻⁵ «mol dm⁻³» ✓

Alternative 2:
«pH = pK_a + log $\frac{\left[{\mathrm{HCOO}}^{-}\right]}{\left[\mathrm{HCOOH}\right]}$»
4.12 = 3.75 + log$\frac{{10}^{-4.12}}{\left[\mathrm{HCOOH}\right]}$ ✓

«[HCOOH] =» 3.24 × 10⁻⁵ «mol dm⁻³» ✓

Award [2] for correct final answer.

Sodium methanoate: basic

Ammonium chloride: acidic

Sodium nitrate: neutral ✓ ✓

Award [2] for three correct.

Award [1] for two correct.

State the electron configuration of the Cu⁺ ion.

Copper(II) chloride is used as a catalyst in the production of chlorine from hydrogen chloride.

4HCl (g) + O₂ (g) → 2Cl₂ (g) + 2H₂O (g)

Calculate the standard enthalpy change, ΔH^θ, in kJ, for this reaction, using section 12 of the data booklet.

The diagram shows the Maxwell–Boltzmann distribution and potential energy profile for the reaction without a catalyst.

Annotate both charts to show the activation energy for the catalysed reaction, using the label E_{a (cat)}.

Explain how the catalyst increases the rate of the reaction.

Solid copper(II) chloride absorbs moisture from the atmosphere to form a hydrate of formula CuCl₂•$x$H₂O.

A student heated a sample of hydrated copper(II) chloride, in order to determine the value of $x$. The following results were obtained:

Mass of crucible = 16.221 g
Initial mass of crucible and hydrated copper(II) chloride = 18.360 g
Final mass of crucible and anhydrous copper(II) chloride = 17.917 g

Determine the value of $x$.

State how current is conducted through the wires and through the electrolyte.

Wires: 

Electrolyte:

Write the half-equation for the formation of gas bubbles at electrode 1.

Bubbles of gas were also observed at another electrode. Identify the electrode and the gas.

Electrode number (on diagram):

Name of gas: 

Deduce the half-equation for the formation of the gas identified in (c)(iii).

Determine the enthalpy of solution of copper(II) chloride, using data from sections 18 and 20 of the data booklet.

The enthalpy of hydration of the copper(II) ion is −2161 kJ mol⁻¹.

Calculate the cell potential at 298 K for the disproportionation reaction, in V, using section 24 of the data booklet.

Comment on the spontaneity of the disproportionation reaction at 298 K.

Calculate the standard Gibbs free energy change, ΔG^θ, to two significant figures, for the disproportionation at 298 K. Use your answer from (e)(i) and sections 1 and 2 of the data booklet.

Suggest, giving a reason, whether the entropy of the system increases or decreases during the disproportionation.

Deduce, giving a reason, the sign of the standard enthalpy change, ΔH^θ, for the disproportionation reaction at 298 K.

Predict, giving a reason, the effect of increasing temperature on the stability of copper(I) chloride solution.

Describe how the blue colour is produced in the Cu(II) solution. Refer to section 17 of the data booklet.

Deduce why the Cu(I) solution is colourless.

When excess ammonia is added to copper(II) chloride solution, the dark blue complex ion, [Cu(NH₃)₄(H₂O)₂]²⁺, forms.

State the molecular geometry of this complex ion, and the bond angles within it.

Molecular geometry:

Bond angles: 

Examine the relationship between the Brønsted–Lowry and Lewis definitions of a base, referring to the ligands in the complex ion [CuCl₄]²⁻.

[Ar] 3d¹⁰
OR
1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ ✔

ΔH^θ = ΣΔH^θ_f (products) − ΣΔH^θ_f (reactants) ✔
ΔH^θ = 2(−241.8 «kJ mol⁻¹») − 4(−92.3 «kJ mol⁻¹») = −114.4 «kJ» ✔

NOTE: Award [2] for correct final answer.

E_{a (cat)} to the left of E_a ✔                        

peak lower AND E_{a (cat)} smaller ✔

«catalyst provides an» alternative pathway ✔

«with» lower E_a
OR
higher proportion of/more particles with «kinetic» E ≥ E_a(cat) «than E_a» ✔

mass of H₂O = «18.360 g – 17.917 g =» 0.443 «g» AND mass of CuCl₂ = «17.917 g – 16.221 g =» 1.696 «g» ✔

moles of H₂O = «$\frac{0.443 \text{g}}{18.02 \text{g\hspace{0.05em}mo}{\text{l}}^{-1}}$=» 0.0246 «mol»
OR
moles of CuCl₂ =«$\frac{1.696 \text{g}}{134.45 \text{g\hspace{0.05em}mo}{\text{l}}^{-1}}$= » 0.0126 «mol» ✔

«water : copper(II) chloride = 1.95 : 1»

«$x$ =» 2 ✔

NOTE: Accept «$x$ =» 1.95.

NOTE: Award [3] for correct final answer.

Wires:
«delocalized» electrons «flow» ✔

Electrolyte:
«mobile» ions «flow» ✔

2Cl⁻ → Cl₂ (g) + 2e⁻
OR
Cl⁻ → $\frac{1}{2}$Cl₂ (g) + e⁻ ✔

NOTE: Accept e for e⁻.

«electrode» 3 AND oxygen/O₂ ✔

NOTE: Accept chlorine/Cl₂.

2H₂O (l) → 4H⁺ (aq) + O₂ (g) + 4e^– ✔

NOTE: Accept 2Cl^– (aq) → Cl₂ (g) + 2e^–.
Accept 4OH⁻ → 2H₂O + O₂ + 4e⁻

enthalpy of solution = lattice enthalpy + enthalpies of hydration «of Cu²⁺ and Cl⁻» ✔

«+2824 kJ mol^–1 − 2161 kJ mol^–1 − 2(359 kJ mol^–1) =» −55 «kJ mol^–1» ✔

NOTE: Accept enthalpy cycle.
Award [2] for correct final answer.

E^θ = «+0.52 – 0.15 = +» 0.37 «V» ✔

spontaneous AND E^θ positive ✔

ΔG^θ = «−nFE = −1 mol × 96 500 C Mol^–1 × 0.37 V=» −36 000 J/−36 kJ ✔

NOTE: Accept “−18 kJ mol^–1 «per mole of Cu⁺»”.

Do not accept values of n other than 1.

Apply SF in this question.

Accept J/kJ or J mol⁻¹/kJ mol⁻¹ for units.

2 mol (aq) → 1 mol (aq) AND decreases ✔

NOTE: Accept “solid formed from aqueous solution AND decreases”.
Do not accept 2 mol → 1 mol without (aq).

ΔG^θ < 0 AND ΔS^θ < 0 AND ΔH^θ < 0
OR
ΔG^θ + TΔS^θ < 0 AND ΔH^θ < 0 ✔

TΔS more negative «reducing spontaneity» AND stability increases ✔

NOTE: Accept calculation showing non-spontaneity at 433 K.

«ligands cause» d-orbitals «to» split ✔

light absorbed as electrons transit to higher energy level «in d–d transitions»
OR
light absorbed as electrons promoted ✔

energy gap corresponds to «orange» light in visible region of spectrum ✔

colour observed is complementary ✔

full «3»d sub-level/orbitals
OR
no d–d transition possible «and therefore no colour» ✔

octahedral AND 90° «180° for axial» ✔

NOTE: Accept square-based bi-pyramid.

Any two of:
ligand/chloride ion Lewis base AND donates e-pair ✔
not Brønsted–Lowry base AND does not accept proton/H⁺ ✔
Lewis definition extends/broader than Brønsted–Lowry definition ✔

Explain the decrease in atomic radius from Na to Cl.

Explain why the radius of the sodium ion, Na⁺, is smaller than the radius of the oxide ion, O²⁻.

Sketch a graph to show the relative values of the successive ionization energies of boron.

Predict, giving your reasons, whether Mn²⁺ or Fe²⁺ is likely to have a more exothermic enthalpy of hydration.

nuclear charge/number of protons/Z_eff increases «causing a stronger pull on the outer electrons» ✔

same number of shells/«outer» energy level/shielding ✔

Accept “atomic number” for “number of protons”.

isoelectronic/same electronic configuration/«both» have 2.8 ✔

more protons in Na⁺ ✔

Sketch showing:

largest increase between third and fourth ionization energies ✔

IE₁ < IE₂ < IE₃ < IE₄ < IE₅ ✔

Fe²⁺ AND smaller size/radius

OR

Fe²⁺ AND higher charge density ✔

stronger interaction with «polar» water molecules ✔

M1 not needed for M2.

Plot the relative values of the first four ionization energies of sodium.

Outline why the alkali metals (group 1) have similar chemical properties.

Describe the structure and bonding in solid sodium oxide.

Calculate values for the following changes using section 8 of the data booklet.

ΔH_atomisation (Na) = 107 kJ mol⁻¹
ΔH_atomisation (O) = 249 kJ mol⁻¹

$\frac{1}{2}$O₂(g) → O^2- (g):

Na (s) → Na⁺ (g):

The standard enthalpy of formation of sodium oxide is −414 kJ mol⁻¹. Determine the lattice enthalpy of sodium oxide, in kJ mol⁻¹, using section 8 of the data booklet and your answers to (d)(i).

(If you did not get answers to (d)(i), use +850 kJ mol⁻¹ and +600 kJ mol⁻¹ respectively, but these are not the correct answers.)

Justify why K₂O has a lower lattice enthalpy (absolute value) than Na₂O.

Write equations for the separate reactions of solid sodium oxide and solid phosphorus(V) oxide with excess water and differentiate between the solutions formed.

Sodium oxide, Na₂O:

Phosphorus(V) oxide, P₄O₁₀:

Differentiation:

Sodium peroxide, Na₂O₂, is formed by the reaction of sodium oxide with oxygen.

2Na₂O (s) + O₂ (g) → 2Na₂O₂ (s)

Calculate the percentage yield of sodium peroxide if 5.00g of sodium oxide produces 5.50g of sodium peroxide.

Determine the enthalpy change, ΔH, in kJ, for this reaction using data from the table and section 12 of the data booklet.

Outline why bond enthalpy values are not valid in calculations such as that in (g)(i).

An allotrope of molecular oxygen is ozone. Compare, giving a reason, the bond enthalpies of the O to O bonds in O₂ and O₃.

Outline why a real gas differs from ideal behaviour at low temperature and high pressure.

The reaction of sodium peroxide with excess water produces hydrogen peroxide and one other sodium compound. Suggest the formula of this compound.

State the oxidation number of carbon in sodium carbonate, Na₂CO₃.

     [✔]

Notes: Accept curve showing general trend.
Award mark only if the energy difference between the first two points is larger than that between points 2/3 and 3/4.

same number of electrons in outer shell

OR

all are s¹ [✔]

«3-D/giant» regularly repeating arrangement «of ions»
OR
lattice «of ions»    [✔]

electrostatic attraction between oppositely charged ions
OR
electrostatic attraction between Na⁺ and O²⁻ ions    [✔]

Note: Do not accept “ionic” without description.

$\frac{1}{2}$O₂(g) → O^2- (g)

«ΔH_atomisation (O) + 1st EA + 2nd EA = 249 k Jmol⁻¹ − 141 kJmol⁻¹ + 753 kJmol⁻¹ =» «+»861 «kJmol⁻¹»    [✔]

Na (s) → Na⁺ (g)

«ΔH_atomisation (Na) + 1st IE = 107 kJmol⁻¹ + 496 kJmol⁻¹ =» «+»603 «kJmol⁻¹»     [✔]

lattice enthalpy = 861 «kJ mol⁻¹» + 2 × 603 «kJ mol⁻¹» −(−414 «kJ mol⁻¹»)     [✔]

«= +» 2481 «kJ mol⁻¹»    [✔]

Note: Award [2] for correct final answer.

If given values are used:
M1: lattice enthalpy = 850 «kJ mol⁻¹» +
2 × 600 «kJ mol⁻¹» −(−414 «kJ mol⁻¹»)
M2: «= +» 2464 «kJ mol⁻¹»

K⁺ ion is larger than Na⁺

OR

smaller attractive force because of greater distance between ion «centres»      [✔]

Sodium oxide:
Na₂O(s) + H₂O(l) → 2NaOH (aq)      [✔]

Phosphorus(V) oxide:
P₄O₁₀ (s) + 6H₂O(l) → 4H₃PO₄ (aq)     [✔]

Differentiation:
NaOH/product of Na₂O is alkaline/basic/pH > 7 AND H₃PO₄/product of P₄O₁₀ is acidic/pH < 7     [✔]

n(Na₂O₂) theoretical yield «= $\frac{5.00\text{g}}{61.98\text{g mo}{\text{l}}^{-1}}$» = 0.0807/8.07 × 10⁻² «mol»

OR

mass of Na₂O₂ theoretical yield «= $\frac{5.00\text{g}}{61.98\text{g mo}{\text{l}}^{-1}}$ × 77.98 gmol⁻¹» = 6.291 «g»    [✔]

% yield «= $\frac{5.50\text{g}}{6.291\text{g}}$ × 100» OR « $\frac{0.0705}{0.0807}$ × 100» = 87.4 «%»     [✔]

Note: Award [2] for correct final answer.

∑ΔH_f products = 2 × (−1130.7) / −2261.4 «kJ»    [✔]

∑ΔH_f reactants = 2 × (−510.9) + 2 × (−393.5) / −1808.8 «kJ»     [✔]

ΔH = «∑ΔH_f products − ∑ΔH_f reactants = −2261.4 −(−1808.8) =» −452.6 «kJ»     [✔]

Note: Award [3] for correct final answer.

Award [2 max] for “+ 452.6 «kJ»”.

only valid for covalent bonds

OR

only valid in gaseous state     [✔]

bond in O₃ has lower enthalpy AND bond order is 1.5 «not 2»    [✔]

Note: Accept “bond in ozone is longer”.

Any one of:

finite volume of particles «requires adjustment to volume of gas»     [✔]

short-range attractive forces «overcomes low kinetic energy»    [✔]

NaOH    [✔]

IV    [✔]

Generally well done with a correct plot of ionization energies.

The majority answered correctly stating same number of valence electrons as the reason. Some candidates stated same size or similar ionization energy but the majority scored well.

Many candidates lost one or two marks for missing “electrostatic forces” between “oppositely charged ions”, or “lattice”. Some candidates’ answers referred to covalent bonds and shapes of molecules.

Good performance with typical error being in the calculation for the first equation, ½O2 (g) → O₂⁻ (g), where the value for the first electron affinity of oxygen was left out.

Many candidates earned some credit for ECF based on (d)(i).

Average performance with answers using atomic size rather than ionic size or making reference to electronegativities of K and Na.

An average of 1.1 out of 3 earned here. Many candidates could write a balanced equation for the reaction of sodium oxide with water but not phosphorus(V) oxide. Mediocre performance in identifying the acid/base nature of the solutions formed.

The majority earned one or two marks in finding a % yield.

The average was 2.2 out 3 for this question on enthalpy of formation. Enthalpy calculations were generally well done.

The majority of candidates referred to “bond enthalpy values are average”, rather than not valid for solids or only used for gases.

Some candidates recognized that ozone had a resonance structure but then only compared bond length between ozone and oxygen rather than bond enthalpy.

Few candidates could distinguish the cause for difference in behaviour between real and ideal gases at low temperature or high pressure. Many answers were based on increase in number of collisions or faster rate or movement of gas particles.

Na₂O was a common formula in many candidates’ answers for the product of the reaction of sodium peroxide with water.

The vast majority of candidates could correctly state the oxidation number of carbon in sodium carbonate.

Sketch the Lewis (electron dot) structure of the P₄ molecule, containing only single bonds.

Write an equation for the reaction of white phosphorus (P₄) with chlorine gas to form phosphorus trichloride (PCl₃).

Deduce the electron domain and molecular geometry using VSEPR theory, and estimate the Cl–P–Cl bond angle in PCl₃.

Outline the reason why PCl₅ is a non-polar molecule, while PCl₄F is polar.

Calculate the standard enthalpy change (ΔH^⦵) for the forward reaction in kJ mol⁻¹.

ΔH^⦵_f PCl₃(g) = −306.4 kJ mol⁻¹

ΔH^⦵_f PCl₅(g) = −398.9 kJ mol⁻¹

Calculate the entropy change, ΔS, in J K⁻¹mol⁻¹, for this reaction.

Chemistry 2e, Chpt. 21 Nuclear Chemistry, Appendix G: Standard Thermodynamic Properties for Selected Substances https://openstax.org/books/chemistry-2e/pages/g-standard-thermodynamic-properties-for- selectedsubstances# page_667adccf-f900-4d86-a13d-409c014086ea © 1999-2021, Rice University. Except where otherwise noted, textbooks on this site are licensed under a Creative Commons Attribution 4.0 International License. (CC BY 4.0) https://creativecommons.org/licenses/by/4.0/.

Calculate the Gibbs free energy change (ΔG), in kJ mol⁻¹, for this reaction at 25 °C. Use section 1 of the data booklet.

If you did not obtain an answer in c(i) or c(ii) use −87.6 kJ mol⁻¹ and −150.5 J mol⁻¹K⁻¹ respectively, but these are not the correct answers.

Determine the equilibrium constant, K, for this reaction at 25 °C, referring to section 1 of the data booklet.

If you did not obtain an answer in (c)(iii), use ΔG = –43.5 kJ mol⁻¹, but this is not the correct answer.

State the equilibrium constant expression, K_c, for this reaction.

State, with a reason, the effect of an increase in temperature on the position of this equilibrium.

Accept any diagram with each P joined to the other three.
Accept any combination of dots, crosses and lines.

P₄(s) + 6Cl₂(g) → 4PCl₃(l) ✔

Electron domain geometry: tetrahedral ✔

Molecular geometry: trigonal pyramidal ✔

Bond angle: 100«°» ✔

Accept any value or range within the range 91−108«°» for M3.

PCl₅ is non-polar:

symmetrical
OR
dipoles cancel ✔

PCl₄F is polar:

P–Cl has a different bond polarity than P–F ✔

non-symmetrical «dipoles»
OR
dipoles do not cancel ✔

Accept F more electronegative than/different electronegativity to Cl for M2.

«−398.9 kJ mol⁻¹ − (−306.4 kJ mol⁻¹) =» −92.5 «kJ mol⁻¹» ✔

«ΔS = 364.5 J K^–1mol^–1 – (311.7 J K^–1mol^–1 + 223.0 J K^–1mol^–1)=» –170.2 «J K^–1mol^–1» ✔

«ΔS =» –0.1702 «kJ mol^–1K^–1»
OR
298 «K» ✔

«ΔG = –92.5 kJ mol^–1 – (298 K × –0.1702 kJ mol^–1K^–1) =» –41.8 «kJ mol^–1» ✔

Award [2] for correct final answer.

If –87.6 and -150.5 are used then –42.8.

«ΔG = –41.8 kJ mol^–1 = $-\frac{8.31 \mathrm{J} {\mathrm{mol}}^{-1} {\mathrm{K}}^{-1}}{1000}$ × 298 K × lnK»
OR
«ΔG = –41800 J mol^–1 = –8.31 J mol^–1K^–1 × 298 K × lnK»

«lnK = =» 16.9 ✔

«K = e^16.9 =» 2.19 × 10⁷ ✔

Award [2] for correct final answer.

Accept range of 1.80 × 10⁶–2.60 × 10⁷.

If –43.5 is used then 4.25 × 10⁷.

«K_c =» $\frac{\left[{\mathrm{PCl}}_5\right]}{\left[{\mathrm{PCl}}_3\right]\left[{\mathrm{Cl}}_2\right]}$ ✔

«shifts» left/towards reactants AND «forward reaction is» exothermic/ΔH is negative ✔

Identify a conjugate acid–base pair in the equation.

The value of K_a at 298 K for the first dissociation is 5.01 × 10⁻⁴.

State, giving a reason, the strength of citric acid.

The dissociation of citric acid is an endothermic process. State the effect on the hydrogen ion concentration, [H⁺], and on K_a, of increasing the temperature.

Calculate the standard Gibbs free energy change, $\mathrm{\Delta }{G}^{\text{θ}}$, in kJ mol⁻¹, for the first dissociation of citric acid at 298 K, using section 1 of the data booklet.

Comment on the spontaneity of the reaction at 298 K.

Outline two laboratory methods of distinguishing between solutions of citric acid and hydrochloric acid of equal concentration, stating the expected observations.

C₆H₈O₇ AND C₆H₇O₇⁻
OR
H₂O AND H₃O⁺ ✔

weak acid AND partially dissociated
OR
weak acid AND equilibrium lies to left
OR
weak acid AND K_a < 1 ✔

«$\mathrm{\Delta }{G}^{\text{θ}}$ = −RT ln K = −8.31 J K^–1 mol^–1 × 298 K × ln(5.01 × 10^–4) ÷ 1000 =» 18.8 «kJ mol^–1» ✔

non-spontaneous AND $\mathrm{\Delta }{G}^{\text{θ}}$ positive ✔

Any two of:

«electrical» conductivity AND HCl greater ✔

pH AND citric acid higher ✔

titrate with strong base AND pH at equivalence higher for citric acid ✔

add reactive metal/carbonate/hydrogen carbonate AND stronger effervescence/faster reaction with HCl ✔

titration AND volume of alkali for complete neutralisation greater for citric acid ✔

titrate with strong base AND more than one equivalence point for complete neutralisation of citric acid ✔

titrate with strong base AND buffer zone with citric acid ✔

NOTE: Accept “add universal indicator AND HCl more red/pink” for M2.

Accept any acid reaction AND HCl greater rise in temperature.

Accept specific examples throughout.

Do not accept “smell” or “taste”.

Explain why, as the reaction proceeds, the pressure increases by the amount shown.

Outline, in terms of collision theory, how a decrease in pressure would affect the rate of reaction.

Deduce how the rate of reaction at t = 2 would compare to the initial rate.

It has been suggested that the reaction occurs as a two-step process:

Step 1: N₂O (g) → N₂ (g) + O (g)

Step 2: N₂O (g) + O (g) → N₂ (g) + O₂ (g)

Explain how this could support the observed rate expression.

The experiment is repeated using the same amount of dinitrogen monoxide in the same apparatus, but at a lower temperature.

Sketch, on the axes in question 2, the graph that you would expect.

The experiment gave an error in the rate because the pressure gauge was inaccurate.

Outline whether repeating the experiment, using the same apparatus, and averaging the results would reduce the error.

The graph below shows the Maxwell–Boltzmann distribution of molecular energies at a particular temperature.

The rate at which dinitrogen monoxide decomposes is significantly increased by a metal oxide catalyst.

Annotate and use the graph to outline why a catalyst has this effect.

Determine the standard entropy change, in J K−1, for the decomposition of dinitrogen monoxide.

2N₂O (g) → 2N₂ (g) + O₂ (g)

Dinitrogen monoxide has a positive standard enthalpy of formation, ΔH_f^θ.

Deduce, giving reasons, whether altering the temperature would change the spontaneity of the decomposition reaction.

increase in the amount/number of moles/molecules «of gas»     [✔]

from 2 to 3/by 50 %     [✔]

«rate of reaction decreases»
concentration/number of molecules in a given volume decreases
OR
more space between molecules    [✔]

collision rate/frequency decreases
OR
fewer collisions per unit time     [✔]

Note: Do not accept just “larger space/volume” for M1.

half «of the initial rate»    [✔]

Note: Accept “lower/slower «than initial rate»”.

1 slower than 2
OR
1 rate determinant step/RDS    [✔]

1 is unimolecular/involves just one molecule so it must be first order
OR
if 1 faster/2 RDS, second order in N₂O
OR
if 1 faster/2 RDS, first order in O     [✔]

smaller initial gradient     [✔]

initial pressure is lower AND final pressure of gas lower «by similar factor»     [✔]

no AND it is a systematic error/not a random error

OR

no AND «a similar magnitude» error would occur every time     [✔]

catalysed and uncatalysed E_a marked on graph AND with the catalysed being at lower energy     [✔]

«for catalysed reaction» greater proportion of/more molecules have E ≥ E_a / E > E_a
OR
«for catalysed reaction» greater area under curve to the right of the E_a     [✔]

Note: Accept “more molecules have the activation energy”.

ΔS^θ = 2(S^θ(N₂)) + S^θ(O₂) – 2(S^θ(N₂O))
OR
ΔS^θ = 2 × 193 «J mol^-1 K^-1» + 205 «J mol^-1 K^-1» – 2 × 220 «J mol^-1 K^-1»     [✔]

«ΔS^θ = +»151 «J K^-1»     [✔]

Note: Award [2] for correct final answer.

exothermic decomposition
OR
ΔH_{(decomposition)} < 0    [✔]

TΔS^θ > ΔH^θ
OR
ΔG^θ «= ΔH^θ – TΔS^θ» < 0 «at all temperatures»     [✔]

reaction spontaneous at all temperatures    [✔]

Students were able in general to relate more moles of gas to increase in pressure.

Few students were able to relate the effect of reduced pressure at constant volume with a decrease in concentration of gas molecules and mostly did not even refer to this, but rather concentrated on lower rate of reaction and frequency of collisions. Many candidates lost a mark by failing to explain rate as collisions per unit time, frequency, etc.

Though the differential equation was considered to be misleading by teachers, most candidates attempted to answer this question, and more than half did so correctly, considering they had the graph to visualize the gradient.

Most students were able to identity step 1 as the RDS/slow but few mentioned unimolecularity or referred vaguely to NO₂ as the only reagent (which was obvious) and got only 1 mark.

Many students drew a lower initial gradient, but most did not reflect the effect of lower temperature on pressure at constant volume and started and finished the curve at the same pressure as the original one.

Almost all candidates identified the inaccurate pressure gauge as a systematic error, thus relating accuracy to this type of error.

The graph was generally well done, but in quite a few cases, candidates did not mention that increase of rate in the catalyzed reaction was due to E (particles) > E_a or did so too vaguely.

Candidates were able to calculate the ΔS of the reaction, though in some cases they failed to multiply by the number of moles.

Though the question asked for decomposition (in bold), most candidates ignored this and worked on the basis of a the ΔH of formation. However, many did write a sound explanation for that situation. On the other hand, in quite a number of cases, they did not state the sign of the ΔH (probably taking it for granted) nor explicitly relate ΔG and spontaneity, which left the examiner with no possibility of evaluating their reasoning.

State why this equilibrium reaction is considered homogeneous.

Predict, giving your reason, the sign of the standard entropy change of the forward reaction.

Calculate the standard Gibbs free energy change, ΔG^Θ, in kJ, for this reaction at 1000 K. Use sections 1 and 2 of the data booklet.

Predict, giving your reasons, whether the forward reaction is endothermic or exothermic. Use your answers to (b) and (c).

0.200 mol sulfur dioxide, 0.300 mol oxygen and 0.500 mol sulfur trioxide were mixed in a 1.00 dm³ flask at 1000 K.

Predict the direction of the reaction showing your working.

all «species» are in same phase ✔

Accept “all species are in same state”.

Accept “all species are gases”.

negative AND fewer moles/molecules «of gas» in the products ✔

ΔG^Θ =«–RT ln K_c =» –8.31 J K^–1 mol^–1 × 1000 K × ln 280

OR

ΔG^Θ = – 4.7 × 10⁴ «J» ✔

«ΔG^Θ =» – 47 «kJ» ✔

Award [2] for correct final answer.

ΔG^Θ < 0/spontaneous AND ΔS^Θ < 0/unfavourable ✔

exothermic AND ΔH^Θ  «must be» negative/favourable ✔

«reaction quotient/Q =» $\frac{{\left[\text{S}{\text{O}}_3\right]}^2}{{\left[\text{S}{\text{O}}_2\right]}^2\left[{\text{O}}_2\right]}\text{/}\frac{{0.500}^2}{{0.200}^2\times 0.300}\text{/}20.8$ ✔

reaction quotient/Q/20.8/answer < K_c/280

OR

mixture needs more product for the number to equal Kc ✔

reaction proceeds to the right/products ✔

Do not award M3 without valid reasoning.

The diagram shows the Maxwell-Boltzmann curve for the uncatalyzed reaction.

Draw a distribution curve at a lower temperature (T₂) and show on the diagram how the addition of a catalyst enables the reaction to take place more rapidly than at T₁.

The hydrogen peroxide could cause further oxidation of the methanol. Suggest a possible oxidation product.

Determine the overall equation for the production of methanol.

8.00 g of methane is completely converted to methanol. Calculate, to three significant figures, the final volume of hydrogen at STP, in dm³. Use sections 2 and 6 of the data booklet.

Determine the enthalpy change, ΔH, in kJ. Use section 11 of the data booklet.

Bond enthalpy of CO = 1077 kJ mol⁻¹.

State one reason why you would expect the value of ΔH calculated from the $∆H_f^{\mathrm{⦵}}$ values, given in section 12 of data booklet, to differ from your answer to (d)(i).

State the expression for K_c for this stage of the reaction.

State and explain the effect of increasing temperature on the value of K_c.

The equilibrium constant, K_c, has a value of 1.01 at 298 K.

Calculate ΔG^⦵, in kJ mol^–1, for this reaction. Use sections 1 and 2 of the data booklet.

Calculate a value for the entropy change, ΔS^⦵, in J K^–1 mol^–1 at 298 K. Use your answers to (e)(i) and section 1 of the data booklet.

If you did not get answers to (e)(i) use –1 kJ, but this is not the correct answer.

Justify the sign of ΔS with reference to the equation.

Predict, giving a reason, how a change in temperature from 298 K to 273 K would affect the spontaneity of the reaction.

curve higher AND to left of T₁ ✔

new/catalysed E_a marked AND to the left of E_a of curve T₁ ✔

Do not penalize curve missing a label, not passing exactly through the origin, or crossing x-axis after E_a.
Do not award M1 if curve drawn shows significantly more/less molecules/greater/smaller area under curve than curve 1.
Accept E_a drawn to T₁ instead of curve drawn as long as to left of marked E_a.

methanoic acid/HCOOH/CHOOH
OR
methanal/HCHO ✔

Accept “carbon dioxide/CO₂”.

CH₄(g) + H₂O(g) $\rightleftharpoons$ CH₃OH(l) + H₂(g) ✔

Accept arrow instead of equilibrium sign.

amount of methane = « $\frac{8.00 \mathrm{g}}{16.05 \mathrm{g} {\mathrm{mol}}^{-1}}$ = » 0.498 «mol» ✔

amount of hydrogen = amount of methane / 0.498 «mol» ✔

volume of hydrogen = «0.498 mol × 22.7 dm³mol⁻¹ = » 11.3 «dm³» ✔

Award [3] for final correct answer.
Award [2 max] for 11.4 «dm³ due to rounding of mass to 16/moles to 0.5. »

Σbonds broken = 4 × 414 «kJ» + 2 × 463 «kJ» / 2582 «kJ» ✔

Σbonds formed = 1077 «kJ» + 3 × 436 «kJ» / 2385 «kJ» ✔

ΔH «= Σbonds broken − Σbonds formed =( 2582 kJ − 2385 kJ)» = «+»197«kJ» ✔

Award [3] for final correct answer.
Award [2 Max] for final answer of −197 «kJ»

bond energies are average values «not specific to the compound» ✔

$K_{\mathit{c}}=\frac{\left[\mathrm{CO}\right]{\left[{\mathrm{H}}_2\right]}^3}{\left[{\mathrm{CH}}_4\right]\left[{\mathrm{H}}_2\mathrm{O}\right]}$ ✔

K_c increases AND «forward» reaction endothermic ✔

«ΔG^⦵ = − RT lnK_c»
ΔG^⦵ = − 8.31 «J K⁻¹ mol⁻¹» × 298 «K» × ln (1.01) / −24.6 «J mol⁻¹» ✔

= −0.0246 «kJ mol^–1» ✔

Award [2] for correct final answer.

Award [1 max] for +0.0246 «kJ mol^–1».

«ΔG^⦵ = ΔH^⦵ − TΔS^⦵»

ΔG^⦵ = −129 «kJ mol^–1» − (298 «K» × ΔS) = −0.0246 «kJ mol^–1» ✔

ΔS^⦵ = « $\frac{\left(129 \mathrm{kJ} {\mathrm{mol}}^{-1}+0.0246 \mathrm{kJ} {\mathrm{mol}}^{-1}\right)\times {10}^3}{298 \mathrm{K}}$ = » −433 «J K^–1 mol^–1» ✔

Award [2] for correct final answer.

Award [1 max] for “−0.433 «kJ K^–1mol^–1»”.

Award [1 max] for “433” or “+433” «J K^–1 mol^–1».

Award [2] for −430 «J K^–1 mol^–1» (result from given values).

«negative as» product is liquid and reactants gases
OR
fewer moles of gas in product ✔

reaction «more» spontaneous/ΔG negative/less positive AND effect of negative entropy decreases/TΔS increases/is less negative/more positive
OR
reaction «more» spontaneous/ΔG negative/less positive AND reaction exothermic «so K_c increases » ✔

Award mark if correct calculation shown.

Deduce the expression for the equilibrium constant, K_c, for this equation.

State how the use of a catalyst affects the position of the equilibrium.

With reference to the reaction quotient, Q, explain why the percentage yield increases as the pressure is increased at constant temperature.

Determine the enthalpy change, ΔH, for the Haber–Bosch process, in kJ. Use Section 11 of the data booklet.

Outline why the value obtained in (b)(i) might differ from a value calculated using ΔH_f data.

Demonstrate that your answer to (b)(i) is consistent with the effect of an increase in temperature on the percentage yield, as shown in the graph.

State, giving a reason, whether the reaction is spontaneous or not at 298 K.

Calculate the value of the equilibrium constant, K, at 298 K. Use sections 1 and 2 of the data booklet.

Calculate the entropy change for the Haber–Bosch process, in J mol^–1K^–1 at 298 K. Use your answer to (b)(i) and section 1 of the data booklet.

Outline, with reference to the reaction equation, why this sign for the entropy change is expected.

$K_c=\frac{{\left[N{H}_3\right]}^2}{\left[N_2\right]{\left[H_2\right]}^3}$ ✔

same/unaffected/unchanged ✔

increasing pressure increases «all» concentrations
OR
increasing pressure decreases volume ✔

Q becomes less than K_c
OR
affects the lower line/denominator of Q expression more than upper line/numerator ✔

«for Q to once again equal K_c,» ratio of products to reactants increases
OR
«for Q to once again equal K_c,» equilibrium shifts to right/products ✔

Award [2 max] for answers that do not refer to Q.

bonds broken: N≡N + 3(H-H) /«1 mol×»945 «kJ mol^–1» + 3«mol»×436 «kJ mol^–1» / 945 «kJ» + 1308 «kJ» / 2253 «kJ» ✔

bonds formed: 6(N-H) / 6«mol»×391 «kJ mol^–1» / 2346 «kJ» ✔

ΔH = «2253 kJ - 2346 kJ = » -93 «kJ» ✔

Award [2 max] for (+)93 «kJ».

«N-H» bond enthalpy is an average «and may not be the precise value in NH₃» ✔

Accept ΔH_f data are more accurate / are not average values.

increased temperature decreases yield «as shown on graph» ✔

shifts equilibrium in endothermic/reverse direction ✔

spontaneous AND ΔG < 0 ✔

$\ln K=⟨⟨\frac{∆G}{R.T}=⟩⟩ -\frac{-33000}{8.31x298} /«+»13.3$ ✔

$K = 6.13\times {10}^5$ ✔

Award [2] for correct final answer.

Accept answers in the range 4.4×10⁵ to 6.2×10⁵ (arises from rounding of ln K).

ΔG = «ΔH – TΔS =» –93000 «J» – 298«K» × ΔS = –33000 ✔

ΔS = 〈〈$\frac{-93000 \mathrm{J} -\left(-33000 \mathrm{J}\right)}{298 \mathrm{K}}$〉〉 = –201 «J mol^–1K^–1» ✔

Do not penalize failure to convert kJ to J in both (c)(ii) and (c)(iii).

Award [2] for correct final answer

Award [1 max] for (+) 201 «J mol^–1 K^–1».

Award [2] for –101 or –100.5 «J mol^–1 K^–1».

«forward reaction involves» decrease in number of moles «of gas» ✔

Deducing the equilibrium constant expression for the given equation was done very well.

Good performance; however, some misread the question as asking for the effect of a catalyst on equilibrium, rather than on the position of equilibrium.

Mediocre performance; very few identified the effect of increasing pressure on all concentrations. Consequently, Q becomes less than K_c (it affects the denominator of Q expression more than the numerator) was not addressed. Question was often answered with respect to kinetics, namely greater frequency of collisions and speed of reaction rather than from equilibrium perspective based on effect of increase in pressure on concentrations.

Good performance; often the bond energy for single N–N bond instead of using it for the triple bond and not taking into consideration the coefficient of three in calculation of bond enthalpies of ammonia. Also, instead of using BE of bonds broken minus those that were formed, the operation was often reversed. Students should be encouraged to draw the Lewis structures in the equations first to determine the bonds being broken and formed.

Outlining why ΔH_rxn based on BE values differ due to being average compared to using ΔH_f values was generally done well.

Good performance; some did not relate that increased temperature decreases yield «as shown on graph» and others arrived at incorrect shift in equilibrium for the reaction.

Reason for the reaction being spontaneous was generally very done well indeed.

Good performance; for lnK calculation in the equation ΔG = RTlnK, ΔG unit had to be converted from kJ to J. This led to an error of 1000 in the value of lnK for some.

Very good performance; since the unit for S is J mol^˗1 K^˗1, ΔG and ΔH needed to be converted from kJ to J, but that was not done in some cases.

Average performance for sign of the entropy change expected for the reaction. Some answers were based on ΔG value rather than in terms of decrease in number of moles of gas or had no idea how to address the question.

(i) Calculate ΔH^θ, in kJ, for this similar reaction below using $\mathrm{\Delta }{H}_{\mathrm{f}}^{\theta }$ data from section 12 of the data booklet. $\mathrm{\Delta }{H}_{\mathrm{f}}^{\theta }$ of HOCH₂CH₂OH(l) is –454.8kJmol^-1.

2CO (g) + 3H₂ (g) $\rightleftharpoons$ HOCH₂CH₂OH (l)

(ii) Deduce why the answers to (a)(iii) and (b)(i) differ.

(iii) ΔS^θ for the reaction in (b)(i) is –620.1JK^-1. Comment on the decrease in entropy.

(iv) Calculate the value of ΔG^θ, in kJ, for this reaction at 298 K using your answer to (b)(i). (If you did not obtain an answer to (b)(i), use –244.0 kJ, but this is not the correct value.)

(v) Comment on the statement that the reaction becomes less spontaneous as temperature is increased.

Predict the ¹HNMR data for ethanedioic acid and ethane-1,2-diol by completing the table.

i
«ΔH = Σ ΔH_f products – ΣΔH_f reactants = –454.8 kJ mol^-1 – 2(–110.5 kJ mol^-1) =» –233.8 «kJ»

ii
in (a)(iii) gas is formed and in (b)(i) liquid is formed
OR
products are in different states
OR
conversion of gas to liquid is exothermic
OR
conversion of liquid to gas is endothermic
OR
enthalpy of vapourisation needs to be taken into account

Accept product is «now» a liquid.
Accept answers referring to bond enthalpies being means/averages.

iii
«ΔS is negative because five mols of» gases becomes «one mol of» liquid
OR
increase in complexity of product «compared to reactants»
OR
product more ordered «than reactants»

Accept “fewer moles of gas” but not “fewer molecules”.

iv
ΔS = $\left(\frac{-620.1}{1000}\right)$«kJ K^-1»
ΔG = –233.8 kJ – (298 K $\left(\frac{-620.1}{1000}\right)$ kJ K^-1) = –49.0 «kJ»

Award [2] for correct final answer.
Award [1 max] for «+»185 × 10³.

If –244.0 kJ used, answer is:
ΔG = –244.0 kJ – (298 K $\left(\frac{-620.1}{1000}\right)$kJ K^-1) = –59.2 «kJ»
Award [2] for correct final answer.

v
increasing T makes ΔG larger/more positive/less negative
OR
–TΔS will increase

Accept “none/no splitting” for singlet.