
SL Paper 2
Points and lie on opposite banks of a river, such that is the shortest distance across the river. Point represents the centre of a city which is located on the riverbank. , and .
The following diagram shows this information.
A boat travels at an average speed of . A bus travels along the straight road between and at an average speed of .
Find the travel time, in hours, from to given that
There is a point , which lies on the road from to , such that . The boat travels from to , and the bus travels from to .
An excursion involves renting the boat and the bus. The cost to rent the boat is per hour, and the cost to rent the bus is per hour.
the boat is taken from to , and the bus from to .
the boat travels directly to .
Find an expression, in terms of for the travel time , from to , passing through .
Find the value of so that is a minimum.
Write down the minimum value of .
Find the new value of so that the total cost to travel from to via is a minimum.
Write down the minimum total cost for this journey.
Markscheme
OR OR (M1)
time (hours)
time (hours) A1
[2 marks]
(A1)
time (hours)
time (hours) A1
[2 marks]
(A1)
(A1)
A1
[3 marks]
valid approach to find the minimum for (may be seen in (iii)) (M1)
graph of OR OR graph of
A1
[2 marks]
(hours) A1
Note: Only allow FT in (b)(ii) and (iii) for and a function that has a minimum in that interval.
[1 mark]
(A1)
valid approach to find the minimum for (may be seen in (ii)) (M1)
graph of OR OR graph of
A1
Note: Only allow FT from (b) if the function has a minimum in .
[3 marks]
A1
Note: Only allow FT from (c)(i) if the function has a minimum in .
[1 mark]
Examiners report
The following table shows the average body weight, , and the average weight of the brain, , of seven species of mammal. Both measured in kilograms (kg).
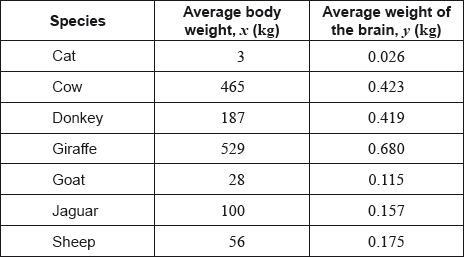
The average body weight of grey wolves is 36 kg.
In fact, the average weight of the brain of grey wolves is 0.120 kg.
The average body weight of mice is 0.023 kg.
Find the range of the average body weights for these seven species of mammal.
For the data from these seven species calculate , the Pearson’s product–moment correlation coefficient;
For the data from these seven species describe the correlation between the average body weight and the average weight of the brain.
Write down the equation of the regression line on , in the form .
Use your regression line to estimate the average weight of the brain of grey wolves.
Find the percentage error in your estimate in part (d).
State whether it is valid to use the regression line to estimate the average weight of the brain of mice. Give a reason for your answer.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(M1)
(A1)(G2)
[2 marks]
(G2)
[2 marks]
(very) strong, positive (A1)(ft)(A1)(ft)
Note: Follow through from part (b)(i).
[2 marks]
(A1)(A1)
Note: Award (A1) for , (A1) for 0.0923.
Award a maximum of (A1)(A0) if the answer is not an equation in the form .
[2 marks]
(M1)
Note: Award (M1) for substituting 36 into their equation.
(A1)(ft)(G2)
Note: Follow through from part (c). The final (A1) is awarded only if their answer is positive.
[2 marks]
(M1)
Note: Award (M1) for their correct substitution into percentage error formula.
(A1)(ft)(G2)
Note: Follow through from part (d). Do not accept a negative answer.
[2 marks]
Not valid (A1)
the mouse is smaller/lighter/weighs less than the cat (lightest mammal) (R1)
OR
as it would mean the mouse’s brain is heavier than the whole mouse (R1)
OR
0.023 kg is outside the given data range. (R1)
OR
Extrapolation (R1)
Note: Do not award (A1)(R0). Do not accept percentage error as a reason for validity.
[2 marks]
Examiners report
The marks obtained by nine Mathematical Studies SL students in their projects (x) and their final IB examination scores (y) were recorded. These data were used to determine whether the project mark is a good predictor of the examination score. The results are shown in the table.
The equation of the regression line y on x is y = mx + c.
A tenth student, Jerome, obtained a project mark of 17.
Use your graphic display calculator to write down , the mean project mark.
Use your graphic display calculator to write down , the mean examination score.
Use your graphic display calculator to write down r , Pearson’s product–moment correlation coefficient.
Find the exact value of m and of c for these data.
Show that the point M (, ) lies on the regression line y on x.
Use the regression line y on x to estimate Jerome’s examination score.
Justify whether it is valid to use the regression line y on x to estimate Jerome’s examination score.
In his final IB examination Jerome scored 65.
Calculate the percentage error in Jerome’s estimated examination score.
Markscheme
14 (G1)
[1 mark]
54 (G1)
[1 mark]
0.5 (G2)
[2 marks]
m = 0.875, c = 41.75 (A1)(A1)
Note: Award (A1) for 0.875 seen. Award (A1) for 41.75 seen. If 41.75 is rounded to 41.8 do not award (A1).
[2 marks]
y = 0.875(14) + 41.75 (M1)
Note: Award (M1) for their correct substitution into their regression line. Follow through from parts (a)(i) and (b)(i).
= 54
and so the mean point lies on the regression line (A1)
(accept 54 is , the mean value of the y data)
Note: Do not award (A1) unless the conclusion is explicitly stated and the 54 seen. The (A1) can be awarded only if their conclusion is consistent with their equation and it lies on the line.
The use of 41.8 as their c value precludes awarding (A1).
OR
54 = 0.875(14) + 41.75 (M1)
54 = 54
Note: Award (M1) for their correct substitution into their regression line. Follow through from parts (a)(i) and (b)(i).
and so the mean point lies on the regression line (A1)
Note: Do not award (A1) unless the conclusion is explicitly stated. Follow through from part (a).
The use of 41.8 as their c value precludes the awarding of (A1).
[2 marks]
y = 0.875(17) + 41.75 (M1)
Note: Award (M1) for correct substitution into their regression line.
= 56.6 (56.625) (A1)(ft)(G2)
Note: Follow through from part (b)(i).
[2 marks]
the estimate is valid (A1)
since this is interpolation and the correlation coefficient is large enough (R1)
OR
the estimate is not valid (A1)
since the correlation coefficient is not large enough (R1)
Note: Do not award (A1)(R0). The (R1) may be awarded for reasoning based on strength of correlation, but do not accept “correlation coefficient is not strong enough” or “correlation is not large enough”.
Award (A0)(R0) for this method if no numerical answer to part (a)(iii) is seen.
[2 marks]
(M1)
Note: Award (M1) for correct substitution into percentage error formula. Follow through from part (c)(i).
= 12.9 (%)(12.9230…) (A1)(ft)(G2)
Note: Follow through from part (c)(i). Condone use of percentage symbol.
Award (G0) for an answer of −12.9 with no working.
[2 marks]
Examiners report
A pan, in which to cook a pizza, is in the shape of a cylinder. The pan has a diameter of 35 cm and a height of 0.5 cm.
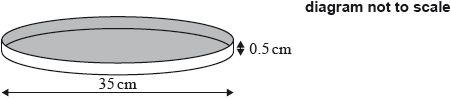
A chef had enough pizza dough to exactly fill the pan. The dough was in the shape of a sphere.
The pizza was cooked in a hot oven. Once taken out of the oven, the pizza was placed in a dining room.
The temperature, , of the pizza, in degrees Celsius, °C, can be modelled by
where is a constant and is the time, in minutes, since the pizza was taken out of the oven.
When the pizza was taken out of the oven its temperature was 230 °C.
The pizza can be eaten once its temperature drops to 45 °C.
Calculate the volume of this pan.
Find the radius of the sphere in cm, correct to one decimal place.
Find the value of .
Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.
Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.
In the context of this model, state what the value of 19 represents.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1)(M1)
Notes: Award (A1) for 17.5 (or equivalent) seen.
Award (M1) for correct substitutions into volume of a cylinder formula.
(A1)(G2)
[3 marks]
(M1)
Note: Award (M1) for equating their answer to part (a) to the volume of sphere.
(M1)
Note: Award (M1) for correctly rearranging so is the subject.
(A1)(ft)(G2)
Note: Award (A1) for correct unrounded answer seen. Follow through from part (a).
(A1)(ft)(G3)
Note: The final (A1)(ft) is awarded for rounding their unrounded answer to one decimal place.
[4 marks]
(M1)
Note: Award (M1) for correct substitution.
(A1)(G2)
[2 marks]
(M1)
Note: Award (M1) for correct substitution into the function, . Follow through from part (c). The negative sign in the exponent is required for correct substitution.
(°C) (°C)) (A1)(ft)(G2)
[2 marks]
(M1)
Note: Award (M1) for equating 45 to the exponential equation and for correct substitution (follow through for their in part (c)).
(A1)(ft)(G1)
(A1)(ft)(G2)
Note: Award final (A1)(ft) for converting their minutes into seconds.
[3 marks]
the temperature of the (dining) room (A1)
OR
the lowest final temperature to which the pizza will cool (A1)
[1 mark]
Examiners report
Abdallah owns a plot of land, near the river Nile, in the form of a quadrilateral ABCD.
The lengths of the sides are and angle .
This information is shown on the diagram.

The formula that the ancient Egyptians used to estimate the area of a quadrilateral ABCD is
.
Abdallah uses this formula to estimate the area of his plot of land.
Show that correct to the nearest metre.
Calculate angle .
Find the area of ABCD.
Calculate Abdallah’s estimate for the area.
Find the percentage error in Abdallah’s estimate.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(M1)
Note: Award (M1) for correct substitution into Pythagoras.
Accept correct substitution into cosine rule.
(A1)
(AG)
Note: Both the rounded and unrounded value must be seen for the (A1) to be awarded.
[2 marks]
(M1)(A1)
Note: Award (M1) for substitution into cosine formula, (A1) for correct substitutions.
(A1)(G2)
[3 marks]
(M1)(M1)(A1)(ft)
Note: Award (M1) for correct substitution into right-angle triangle area. Award (M1) for substitution into area of triangle formula and (A1)(ft) for correct substitution.
(A1)(ft)(G3)
Notes: Follow through from part (b).
[4 marks]
(M1)
Note: Award (M1) for correct substitution in the area formula used by ‘Ancient Egyptians’.
(A1)(G2)
[2 marks]
(M1)
Notes: Award (M1) for correct substitution into percentage error formula.
(A1)(ft)(G2)
Notes: Follow through from parts (c) and (d)(i).
[2 marks]
Examiners report
Olivia’s house consists of four vertical walls and a sloping roof made from two rectangles. The height, , from the ground to the base of the roof is 4.5 m.
The base angles of the roof are and .
The house is 10 m long and 5 m wide.
The length is approximately 2.84 m.
Olivia decides to put solar panels on the roof. The solar panels are fitted to both sides of the roof.
Each panel is 1.6 m long and 0.95 m wide. All the panels must be arranged in uniform rows, with the shorter edge of each panel parallel to or . Each panel must be at least 0.3 m from the edge of the roof and the top of the roof, .
Olivia estimates that the solar panels will cover an area of 29 m2.
Find the length , giving your answer to four significant figures.
Find the total area of the two rectangles that make up the roof.
Find the maximum number of complete panels that can be fitted to the whole roof.
Find the percentage error in her estimate.
Olivia investigates arranging the panels, such that the longer edge of each panel is parallel to or .
State whether this new arrangement will allow Olivia to fit more solar panels to the roof. Justify your answer.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
180° − 27° − 26° (M1)
Note: Award (M1) for correct working to find angle or 127 seen.
(M1)(A1)
Note: Award (M1) for substitution into sine rule formula and (A1) for correct substitution.
2.74450 (m) (A1)
( =) 2.745 (m) (A1)(ft)(G4)
Note: The final (A1)(ft) is for correctly rounding their unrounded to 4 sf. If 2.745 is given as the final answer, the unrounded answer need not be seen, award (M1)(M1)(A1)(A2). For all other answers, the unrounded answer must be seen to an accuracy greater than 4 sf.
Award (G3) for a final answer of 2.74450…(m) with no working. If radians are used then award at most (M1)(M1)(A1)(A0)(A1)(ft) for an answer of 3.920 (m).
[5 marks]
Units are required in this question part.
10 × 2.84 + 10 × 2.74450… (M1)(M1)
Note: Award (M1) for finding their area of each rectangle and (M1) for adding their areas.
OR
10 × (2.84 + 2.74450…) (M1)(M1)
Note: Award (M1) for adding and their . Award (M1) for multiplying their total area by 10.
55.8 (55.8450…) m2 (A1)(ft)(G3)
Note: Follow through from their in part (a).
[3 marks]
(M1)
Note: Award (M1) for correct calculation of the number of panels on the long side.
OR (M1)
Note: Award (M1) for correct calculation of the number of panels on either short side with no further incorrect working.
20 (A1)(ft)(G2)
Note: Follow through from part (a). Do not award (M0)(M1)(A1)(ft).
[3 marks]
20 × 1.6 × 0.95 (= 30.4) (M1)
Note: Award (M1) for their 20 × 1.6 × 0.95 or 30.4 seen. Follow through from their 20 in part (c). Award (M0) if their 20 is not an integer.
(M1)
Note: Award (M1) for correct substitution of their 30.4 into the percentage error formula. Their 30.4 must be exact.
found. Accept a method in two steps where “×100” is implicit from their answer.
The second (M1) is contingent on the first (M1) being awarded, eg do not award (M0)(M1)(A0).
4.61 (%) (4.60526 (%)) (A1)(ft)(G3)
Note: Follow through from their answer to part (c). Percentage sign is not required.
Award (G2) for an unsupported final answer of 4.61.
[3 marks]
1 × 9 (array) OR 18 (total panels) (R1)(ft)
Note: Award (R1) for one correct array seen (1 × 9) or total number of panels (18). Working is not required, but award (R0) for incorrect working seen. Correct working is as follows.
Reasoning may compare both sides of the roof or just one side; accept correct comparisons with part (c) values. Follow through from their treatment of tolerances in part (c) and maximum number of panels.
Award (R0) for any approach with no clearance or for any method which includes further incorrect working.
No (new arrangement will mean fewer solar panels) (A1)(ft)
Note: Follow through from their maximum number of panels in part (c). Do not award (R0)(A1)(ft).
[2 marks]
Examiners report
A factory packages coconut water in cone-shaped containers with a base radius of 5.2 cm and a height of 13 cm.
The factory designers are currently investigating whether a cone-shaped container can be replaced with a cylinder-shaped container with the same radius and the same total surface area.
Find the volume of one cone-shaped container.
Find the slant height of the cone-shaped container.
Show that the total surface area of the cone-shaped container is 314 cm2, correct to three significant figures.
Find the height, , of this cylinder-shaped container.
The factory director wants to increase the volume of coconut water sold per container.
State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(M1)
Note: Award (M1) for correct substitution in the volume formula for cone.
368 (368.110…) cm3 (A1)(G2)
Note: Accept 117.173… cm3 or cm3.
[2 marks]
(slant height2) = (5.2)2 + 132 (M1)
Note: Award (M1) for correct substitution into the formula.
14.0 (14.0014…) (cm) (A1)(G2)
[2 marks]
14.0014… × (5.2) × + (5.2)2 × (M1)(M1)
Note: Award (M1) for their correct substitution in the curved surface area formula for cone; (M1) for adding the correct area of the base. The addition must be explicitly seen for the second (M1) to be awarded. Do not accept rounded values here as may come from working backwards.
313.679… (cm2) (A1)
Note: Use of 3 sf value 14.0 gives an unrounded answer of 313.656….
314 (cm2) (AG)
Note: Both the unrounded and rounded answers must be seen for the final (A1) to be awarded.
[3 marks]
2 × × (5.2) × + 2 × × (5.2)2 = 314 (M1)(M1)(M1)
Note: Award (M1) for correct substitution in the curved surface area formula for cylinder; (M1) for adding two correct base areas of the cylinder; (M1) for equating their total cylinder surface area to 314 (313.679…). For this mark to be awarded the areas of the two bases must be added to the cylinder curved surface area and equated to 314. Award at most (M1)(M0)(M0) for cylinder curved surface area equated to 314.
( =) 4.41 (4.41051…) (cm) (A1)(G3)
[4 marks]
× (5.2)2 × 4.41051… (M1)
Note: Award (M1) for correct substitution in the volume formula for cylinder.
375 (374.666…) (cm3) (A1)(ft)(G2)
Note: Follow through from part (d).
375 (cm3) > 368 (cm3) (R1)(ft)
OR
“volume of cylinder is larger than volume of cone” or similar (R1)(ft)
Note: Follow through from their answer to part (a). The verbal statement should be consistent with their answers from parts (e) and (a) for the (R1) to be awarded.
replace with the cylinder containers (A1)(ft)
Note: Do not award (A1)(ft)(R0). Follow through from their incorrect volume for the cylinder in this question part but only if substitution in the volume formula shown.
[4 marks]
Examiners report
A water container is made in the shape of a cylinder with internal height cm and internal base radius cm.

The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.
The volume of the water container is .
The water container is designed so that the area to be coated is minimized.
One can of water-resistant material coats a surface area of .
Write down a formula for , the surface area to be coated.
Express this volume in .
Write down, in terms of and , an equation for the volume of this water container.
Show that .
Find .
Using your answer to part (e), find the value of which minimizes .
Find the value of this minimum area.
Find the least number of cans of water-resistant material that will coat the area in part (g).
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1)(A1)
Note: Award (A1) for either OR seen. Award (A1) for two correct terms added together.
[2 marks]
(A1)
Notes: Units not required.
[1 mark]
(A1)(ft)
Notes: Award (A1)(ft) for equating to their part (b).
Do not accept unless is explicitly defined as their part (b).
[1 mark]
(A1)(ft)(M1)
Note: Award (A1)(ft) for their seen.
Award (M1) for correctly substituting only into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to and substituting for in expression for .
(AG)
Notes: The conclusion, , must be consistent with their working seen for the (A1) to be awarded.
Accept as equivalent to .
[2 marks]
(A1)(A1)(A1)
Note: Award (A1) for , (A1) for or , (A1) for .
[3 marks]
(M1)
Note: Award (M1) for equating their part (e) to zero.
OR (M1)
Note: Award (M1) for isolating .
OR
sketch of derivative function (M1)
with its zero indicated (M1)
(A1)(ft)(G2)
[3 marks]
(M1)
Note: Award (M1) for correct substitution of their part (f) into the given equation.
(A1)(ft)(G2)
[2 marks]
(M1)
Note: Award (M1) for dividing their part (g) by 2000.
(A1)(ft)
Notes: Follow through from part (g).
14 (cans) (A1)(ft)(G3)
Notes: Final (A1) awarded for rounding up their to the next integer.
[3 marks]
Examiners report
The Tower of Pisa is well known worldwide for how it leans.
Giovanni visits the Tower and wants to investigate how much it is leaning. He draws a diagram showing a non-right triangle, ABC.
On Giovanni’s diagram the length of AB is 56 m, the length of BC is 37 m, and angle ACB is 60°. AX is the perpendicular height from A to BC.
Giovanni’s tourist guidebook says that the actual horizontal displacement of the Tower, BX, is 3.9 metres.
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree.
Use Giovanni's diagram to calculate the length of AX.
Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
Find the percentage error on Giovanni’s diagram.
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.
Find the angle of elevation of A from D.
Markscheme
(M1)(A1)
Note: Award (M1) for substituting the sine rule formula, (A1) for correct substitution.
angle = 34.9034…° (A1)
Note: Award (A0) if unrounded answer does not round to 35. Award (G2) if 34.9034… seen without working.
angle = 180 − (34.9034… + 60) (M1)
Note: Award (M1) for subtracting their angle BAC + 60 from 180.
85.0965…° (A1)
85° (AG)
Note: Both the unrounded and rounded value must be seen for the final (A1) to be awarded. If the candidate rounds 34.9034...° to 35° while substituting to find angle , the final (A1) can be awarded but only if both 34.9034...° and 35° are seen.
If 85 is used as part of the workings, award at most (M1)(A0)(A0)(M0)(A0)(AG). This is the reverse process and not accepted.
sin 85… × 56 (M1)
= 55.8 (55.7869…) (m) (A1)(G2)
Note: Award (M1) for correct substitution in trigonometric ratio.
(M1)
Note: Award (M1) for correct substitution in the Pythagoras theorem formula. Follow through from part (a)(ii).
OR
cos(85) × 56 (M1)
Note: Award (M1) for correct substitution in trigonometric ratio.
= 4.88 (4.88072…) (m) (A1)(ft)(G2)
Note: Accept 4.73 (4.72863…) (m) from using their 3 s.f answer. Accept equivalent methods.
[2 marks]
(M1)
Note: Award (M1) for correct substitution into the percentage error formula.
= 25.1 (25.1282) (%) (A1)(ft)(G2)
Note: Follow through from part (a)(iii).
[2 marks]
(A1)(ft)(M1)
Note: Award (A1)(ft) for their 40.11927… seen. Award (M1) for correct substitution into trigonometric ratio.
OR
(37 − 4.88072…)2 + 55.7869…2
(AC =) 64.3725…
64.3726…2 + 82 − 2 × 8 × 64.3726… × cos120
(AD =) 68.7226…
(A1)(ft)(M1)
Note: Award (A1)(ft) for their correct values seen, (M1) for correct substitution into the sine formula.
= 54.3° (54.2781…°) (A1)(ft)(G2)
Note: Follow through from part (a). Accept equivalent methods.
[3 marks]
Examiners report
John purchases a new bicycle for 880 US dollars (USD) and pays for it with a Canadian credit card. There is a transaction fee of 4.2 % charged to John by the credit card company to convert this purchase into Canadian dollars (CAD).
The exchange rate is 1 USD = 1.25 CAD.
John insures his bicycle with a US company. The insurance company produces the following table for the bicycle’s value during each year.
The values of the bicycle form a geometric sequence.
During the 1st year John pays 120 USD to insure his bicycle. Each year the amount he pays to insure his bicycle is reduced by 3.50 USD.
Calculate, in CAD, the total amount John pays for the bicycle.
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
Calculate, in years, when the bicycle value will be less than 50 USD.
Find the total amount John has paid to insure his bicycle for the first 5 years.
John purchased the bicycle in 2008.
Justify why John should not insure his bicycle in 2019.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
1.042 × 880 × 1.25 OR (880 + 0.042 × 880) × 1.25 (M1)(M1)
Note: Award (M1) for multiplying 880 by 1.042 and (M1) for multiplying 880 by 1.25.
1150 (CAD) (1146.20 (CAD)) (A1)(G2)
Note: Accept 1146.2 (CAD)
[3 marks]
OR (M1)
Note: Award (M1) for correctly dividing sequential terms to find the common ratio, or 0.8 seen.
880(0.8)5−1 (M1)
Note: Award (M1) for correct substitution into geometric sequence formula.
360.45 (USD) (A1)(G3)
Note: Do not award the final (A1) if the answer is not correct to 2 decimal places. Award at most (M0)(M1)(A0) if .
[3 marks]
(M1)
Note: Award (M1) for correct substitution into geometric sequence formula and (in)equating to 50. Accept weak or strict inequalities. Accept an equation. Follow through from their common ratio in part (b). Accept a sketch of their GP with as a valid method.
OR
AND (M1)
Note: Award (M1) for their and both seen. If the student states , without seen, this is not sufficient to award (M1).
14 or “14th year” or “after the 13th year” (A1)(ft)(G2)
Note: The context of the question requires the final answer to be an integer. Award at most (M1)(A0) for a final answer of 13.9 years. Follow through from their 0.8 in part (b).
[2 marks]
(M1)(A1)
Note: Award (M1) for substitution into arithmetic series formula, (A1) for correct substitution.
565 (USD) (A1)(G2)
[3 marks]
2019 is the 12th year/term (M1)
Note: Award (M1) for 12 seen.
75.59 (value of bicycle) AND 81.5 (cost of insurance policy) (A1)(ft)
Note: Award (A1) for both sequences’ 12th term seen. The value of the bicycle will follow through from their common ratio in part (b). Do not award (M0)(A1).
the cost of the insurance policy is greater than the value of the bicycle (R1)(ft)
Note: Award (R1)(ft) for a reason consistent with their cost of insurance policy and their value of the bicycle. Follow through within this part. Award (R0) if the correct values are not explicitly seen. Accept the following contextualized reasons: “the insurance is not worth it", "the values are too close", "insurance is as much as the value of the bike", but only if their cost of insurance is greater than the value of the bicycle.
OR
75.59 < 81.5 (R1)(ft)
Note: Award (R1)(ft) for a correct numerical comparison showing their cost of insurance policy is greater than their value of the bicycle. Follow through within this part.
[3 marks]
Examiners report
An archaeological site is to be made accessible for viewing by the public. To do this, archaeologists built two straight paths from point A to point B and from point B to point C as shown in the following diagram. The length of path AB is 185 m, the length of path BC is 250 m, and angle is 125°.
The archaeologists plan to build two more straight paths, AD and DC. For the paths to go around the site, angle is to be made equal to 85° and angle is to be made equal to 70° as shown in the following diagram.
Find the distance from A to C.
Find the size of angle .
Find the size of angle .
Find the size of angle .
The length of path AD is 287 m.
Find the area of the region ABCD.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
AC2 = 1852 + 2502 − 2 × 185 × 250 × cos(125°) (M1)(A1)
Note: Award (M1) for substitution in the cosine formula; (A1) for correct substitution.
387 (387.015…) (m) (A1)(G2)
Note: If radians are used the answer is 154 (154.471…), award at most (M1)(A1)(A0).
[3 marks]
(M1)(A1)(ft)
OR
(M1)(A1)(ft)
Note: Award (M1) for substitution in the sine or cosine formulas; (A1)(ft) for correct substitution.
(31.9478…°) (A1)(ft)(G2)
Note: Follow through from part (a).
[3 marks]
(CAD =) 53.1° (53.0521…°) (A1)(ft)
Note: Follow through from their part (b)(i) only if working seen.
[1 mark]
(ACD = ) 70° − (180° − 125° − 31.9478°…) (M1)
Note: Award (M1) for subtracting their angle from 70°.
OR
(ADC =) 360 − (85 + 70 + 125) = 80
(ACD =) 180 − 80 − 53.0521... (M1)
46.9° (46.9478…°) (A1)(ft)(G2)
Note: Follow through from part (b)(i).
[2 marks]
(M1)(M1)(M1)
Note: Award (M1) for substitution in the area formula for either triangle; (M1) for correct substitution for both areas; (M1) for adding their two areas;
18942.8… + 44383.9…
63300 (m2) (63326.8… (m2)) (A1)(ft)(G3)
Note: Follow through from parts (a) and (b)(ii).
OR
M1M1M1
Note: Award (M1) for substitution in the area formula for either triangle; (M1) for correct substitution for both areas; (M1) for adding their two areas;
26446.4… + 36869.3…
63300 (63315.8…) (m2) (A1)(ft)(G3)
[4 marks]