
SL Paper 1
Let , for . The point lies on the graph of .
Let . The point lies on the graph of and is the reflection of point in the line .
The line is tangent to the graph of at .
Write down the coordinates of .
Given that , find the equation of in terms of , and .
The line is tangent to the graph of at and has equation .
The line passes through the point .
The gradient of the normal to at is .
Find the equation of in terms of .
Consider the binomial expansion where and .
Show that .
The third term in the expansion is the mean of the second term and the fourth term in the expansion.
Find the possible values of .
The following diagram shows part of the graph of a quadratic function .
The graph of has its vertex at , and it passes through point as shown.
The function can be written in the form .
The line is tangent to the graph of at .
Now consider another function . The derivative of is given by , where .
Write down the equation of the axis of symmetry.
Write down the values of and .
Point has coordinates . Find the value of .
Find the equation of .
Find the values of for which is an increasing function.
Find the values of for which the graph of is concave-up.
Consider the functions , for , and for .
The following diagram shows the graphs of and .
The graphs of and intersect at points and . The coordinates of are .
In the following diagram, the shaded region is enclosed by the graph of , the graph of , the -axis, and the line , where .
The area of the shaded region can be written as , where .
Find the coordinates of .
Find the value of and the value of .
The following diagram shows the graph of a function , with domain .

The points and lie on the graph of .
On the grid, sketch the graph of .
Olava’s Pizza Company supplies and delivers large cheese pizzas.
The total cost to the customer, , in Papua New Guinean Kina (), is modelled by the function
where , is the number of large cheese pizzas ordered. This total cost includes a fixed cost for delivery.
State, in the context of the question, what the value of represents.
State, in the context of the question, what the value of represents.
Write down the minimum number of pizzas that can be ordered.
Kaelani has .
Find the maximum number of large cheese pizzas that Kaelani can order from Olava’s Pizza Company.
The graph of the quadratic function intersects the -axis at the point and has its vertex at the point .

Write down the equation of the axis of symmetry for this graph.
Find the value of .
Write down the range of .
The following table shows the probability distribution of a discrete random variable , in terms of an angle .

Show that .
Given that , find .
Let , for . The graph of between and is rotated 360° about the -axis. Find the volume of the solid formed.
The function is defined for all . The line with equation is the tangent to the graph of at .
The function is defined for all where and .
Write down the value of .
Find .
Find .
Hence find the equation of the tangent to the graph of at .
A function is defined by , where .
The graph of has a vertical asymptote and a horizontal asymptote.
Write down the equation of the vertical asymptote.
Write down the equation of the horizontal asymptote.
On the set of axes below, sketch the graph of .
On your sketch, clearly indicate the asymptotes and the position of any points of intersection with the axes.
Hence, solve the inequality .
Consider the function , for . The following diagram shows part of the graph of .
For the graph of
find the -coordinates of the -intercepts.
find the coordinates of the vertex.
The function can be written in the form .
Write down the value of and the value of .
Consider the function where and .
The graph of contains the point .
Consider the arithmetic sequence where and .
Show that .
Write down an expression for .
Find the value of .
Show that and are four consecutive terms in a geometric sequence.
Find the value of and the value of .
The diagram shows the graph of the quadratic function , with vertex .
The equation has two solutions. One of these solutions is .
Write down the other solution of .
Complete the table below placing a tick (✔) to show whether the unknown parameters and are positive, zero or negative. The row for has been completed as an example.
State the values of for which is decreasing.
A quadratic function can be written in the form . The graph of has axis of symmetry and -intercept at
Find the value of .
Find the value of .
The line is a tangent to the curve of . Find the values of .
The following diagram shows part of the graph of , for .
Let be any point on the graph of . Line is the tangent to the graph of at .
Line intersects the -axis at point and the -axis at point B.
Find in terms of and .
Show that the equation of is .
Find the area of triangle in terms of .
The graph of is translated by to give the graph of .
In the following diagram:
- point lies on the graph of
- points , and lie on the vertical asymptote of
- points and lie on the horizontal asymptote of
- point lies on the -axis such that is parallel to .
Line is the tangent to the graph of at , and passes through and .
Given that triangle and rectangle have equal areas, find the gradient of in terms of .
A particle moves along the -axis. The velocity of is at time seconds, where for . When is at the origin .
Find the value of when reaches its maximum velocity.
Show that the distance of from at this time is metres.
Sketch a graph of against , clearly showing any points of intersection with the axes.
Find the total distance travelled by .
The following table shows the probability distribution of a discrete random variable where .
Find the value of , justifying your answer.
Let , where and . The line meets the graph of at exactly one point.
The function can be expressed in the form , where .
The function can also be expressed in the form , where .
Show that .
Find the value of and the value of .
Find the value of and the value of .
Hence find the values of where the graph of is both negative and increasing.
A function, , has its derivative given by , where . The following diagram shows part of the graph of .
The graph of has an axis of symmetry .
The vertex of the graph of lies on the -axis.
The graph of has a point of inflexion at .
Find the value of .
Write down the value of the discriminant of .
Hence or otherwise, find the value of .
Find the value of the gradient of the graph of at .
Sketch the graph of , the second derivative of . Indicate clearly the -intercept and the -intercept.
Write down the value of .
Find the values of for which the graph of is concave-down. Justify your answer.
Jean-Pierre jumps out of an airplane that is flying at constant altitude. Before opening his parachute, he goes through a period of freefall.
Jean-Pierre’s vertical speed during the time of freefall, , in , is modelled by the following function.
where , is the number of seconds after he jumps out of the airplane, and is a constant. A sketch of Jean-Pierre’s vertical speed against time is shown below.
Jean-Pierre’s initial vertical speed is .
Find the value of .
In the context of the model, state what the horizontal asymptote represents.
Find Jean-Pierre’s vertical speed after seconds. Give your answer in .
Let and , for , where is a constant.
Find .
Given that , find the value of .
The following diagram shows the graph of for .
A function is defined by for .
Describe a sequence of transformations that transforms the graph of for to the graph of for .
State the range of .
Find an expression for , stating its domain.
Find the coordinates of the point(s) where the graphs of and intersect.
Line intersects the -axis at point A and the -axis at point B, as shown on the diagram.

The length of line segment OB is three times the length of line segment OA, where O is the origin.
Point lies on .
Find the equation of in the form .
Find the -coordinate of point A.
Consider the functions and
The functions intersect at points P and Q. Part of the graph of and part of the graph of are shown on the diagram.
Find the range of f.
Write down the x-coordinate of P and the x-coordinate of Q.
Write down the values of x for which .
Let . The point lies on the graph of .
Find the value of .
The graph of is transformed to obtain the graph of .
Describe this transformation.
Let for .
Consider the function defined by for and its graph .
Show that .
The graph of has a horizontal tangent at point . Find the coordinates of .
Given that , show that is a local maximum point.
Solve for .
Sketch the graph of , showing clearly the value of the -intercept and the approximate position of point .
The following table shows values of and for different values of .
Both and are one-to-one functions.
Find .
Find .
Find the value of such that .
The function is defined by , where .
Write down the equation of
Find the coordinates where the graph of crosses
the vertical asymptote of the graph of .
the horizontal asymptote of the graph of .
the -axis.
the -axis.
Sketch the graph of on the axes below.
Consider the series , where and .
Consider the case where the series is geometric.
Now consider the case where the series is arithmetic with common difference .
Show that .
Given that and , find the value of .
Show that .
Write down in the form , where .
The sum of the first terms of the series is .
Find the value of .
Let and .
Find the values of so that has no real roots.
The functions and are defined such that and .
Show that .
Given that , find the value of .
Let , for , where .
Point lies on the graph of .
Find the value of .
The -intercept of the graph of is .
On the following grid, sketch the graph of .
Consider the graph of the function .
Write down the zero of .
Write down the coordinates of the local minimum point.
Consider the function .
Solve .
The points and have position vectors and respectively.
Point has position vector . Let be the origin.
Find, in terms of ,
.
.
Given that , show that .
Calculate the area of triangle .
The graph of for is shown in the following diagram.
Write down the value of .
Write down the value of .
Let for . On the axes above, sketch the graph of .
Consider the points , and . The line passes through the point and is perpendicular to .
Find the equation of .
The line passes through the point .
Find the value of .
The functions and are defined for by and , where .
Given that and , find the value of and the value of .
Consider the functions where and where .
Find .
Solve the equation where .
Let , for . The following diagram shows part of the graph of .

The graph of crosses the -axis at the origin and at the point .
The line intersects the graph of at another point Q, as shown in the following diagram.

Find the area of the region enclosed by the graph of and the line .
The function is of the form , where , and are positive integers.
Part of the graph of is shown on the axes below. The graph of the function has its local maximum at and its local minimum at .
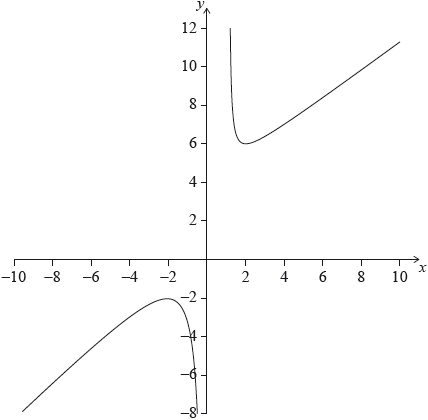
Draw the line on the axes.
Write down the number of solutions to .
Find the range of values of for which has no solution.
Consider the vectors a = and b = .
Find the possible values of p for which a and b are parallel.
Let .
The function can also be expressed in the form .
(i) Write down the value of .
(ii) Find the value of .
Consider the function , with derivative where .
Show that the discriminant of is .
Given that is an increasing function, find all possible values of .
Consider the function defined by for .
The following diagram shows part of the graph of which crosses the -axis at point , with coordinates . The line is the tangent to the graph of at the point .
Find the exact value of .
Given that the gradient of is , find the -coordinate of .