IB Questionbank

Updates to Questionbank

User interface language: English | Español

HL Paper 2

A function $f$ is defined by $f (x) = arcsin (\frac{x^{2} - 1}{x^{2} + 1}), x \in ℝ$ .

A function $g$ is defined by $g (x) = arcsin (\frac{x^{2} - 1}{x^{2} + 1}), x \in ℝ, x \geq 0$ .

Show that $f$ is an even function.

[1]

By considering limits, show that the graph of $y = f (x)$ has a horizontal asymptote and state its equation.

[2]

Show that $f' (x) = \frac{2 x}{\sqrt{x^{2}} (x^{2} + 1)}$ for $x \in ℝ, x \neq 0$ .

[6]

c.i.

By using the expression for $f' (x)$ and the result $\sqrt{x^{2}} = |x|$ , show that $f$ is decreasing for $x < 0$ .

[3]

c.ii.

Find an expression for $g^{- 1} (x)$ , justifying your answer.

[5]

State the domain of $g^{- 1}$ .

[1]

Sketch the graph of $y = g^{- 1} (x)$ , clearly indicating any asymptotes with their equations and stating the values of any axes intercepts.

[3]

Markscheme

EITHER

$f (- x) = arcsin (\frac{{(- x)}^{2} - 1}{{(- x)}^{2} + 1}) = arcsin (\frac{x^{2} - 1}{x^{2} + 1}) = f (x)$ R1

a sketch graph of $y = f (x)$ with line symmetry in the $y$ -axis indicated R1

THEN

so $f (x)$ is an even function. AG

[1 mark]

as $x \to \pm \infty, f (x) \to arcsin 1 (\to \frac{π}{2})$ A1

so the horizontal asymptote is $y = \frac{π}{2}$ A1

[2 marks]

attempting to use the quotient rule to find $\frac{d}{d x} (\frac{x^{2} - 1}{x^{2} + 1})$ M1

$\frac{d}{d x} (\frac{x^{2} - 1}{x^{2} + 1}) = \frac{2 x (x^{2} + 1) - 2 x (x^{2} - 1)}{{(x^{2} + 1)}^{2}} (= \frac{4 x}{{(x^{2} + 1)}^{2}})$ A1

attempting to use the chain rule to find $\frac{d}{d x} (arcsin (\frac{x^{2} - 1}{x^{2} + 1}))$ M1

let $u = \frac{x^{2} - 1}{x^{2} + 1}$ and so $y = arcsin u$ and $\frac{d y}{d u} = \frac{1}{\sqrt{1 - u^{2}}}$

$f' (x) = \frac{1}{\sqrt{1 - {(\frac{x^{2} - 1}{x^{2} + 1})}^{2}}} \times \frac{4 x}{{(x^{2} + 1)}^{2}}$ M1

$= \frac{4 x}{\sqrt{{(x^{2} + 1)}^{2} - {(x^{2} - 1)}^{2}}} \times \frac{1}{(x^{2} + 1)}$ A1

$= \frac{4 x}{\sqrt{4 x^{2}}} \times \frac{1}{(x^{2} + 1)}$ A1

$= \frac{2 x}{\sqrt{x^{2}} (x^{2} + 1)}$ AG

[6 marks]

c.i.

$f' (x) = \frac{2 x}{|x| (x^{2} + 1)}$

EITHER

for $x < 0, |x| = - x$ (A1)

so $f' (x) = - \frac{2 x}{x^{2} + 1}$ A1

$|x| > 0$ and $x^{2} + 1 > 0$ A1

$2 x < 0, x < 0$ A1

THEN

$f' (x) < 0$ R1

Note: Award R1 for stating that in $f' (x)$ , the numerator is negative, and the denominator is positive.

so $f$ is decreasing for $x < 0$ AG

Note: Do not accept a graphical solution

[3 marks]

c.ii.

$x = arcsin (\frac{y^{2} - 1}{y^{2} + 1})$ M1

$sin x = \frac{y^{2} - 1}{y^{2} + 1} \Rightarrow y^{2} sin x + sin x = y^{2} - 1$ A1

$y^{2} = \frac{1 + sin x}{1 - sin x}$ A1

domain of $g$ is $x \in ℝ, x \geq 0$ and so the range of $g^{- 1}$ must be $y \in ℝ, y \geq 0$

hence the positive root is taken (or the negative root is rejected) R1

Note: The R1 is dependent on the above A1.

so $(g^{- 1} (x) =) \sqrt{\frac{1 + sin x}{1 - sin x}}$ A1

Note: The final A1 is not dependent on R1 mark.

[5 marks]

domain is $- \frac{π}{2} \leq x < \frac{π}{2}$ A1

Note: Accept correct alternative notations, for example, $⌊ - \frac{π}{2}, \frac{π}{2} ⌊$ or $⌊ - \frac{π}{2}, \frac{π}{2})$ .
Accept $[- 1.57, 1.57 [$ if correct to $3$ s.f.

[1 mark]

A1A1A1

Note: A1 for correct domain and correct range and $y$ -intercept at $y = 1$
A1 for asymptotic behaviour $x \to \frac{π}{2}$
A1 for $x = \frac{π}{2}$
Coordinates are not required.
Do not accept $x = 1.57$ or other inexact values.

[3 marks]

Examiners report

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

Show that ${\text{cot}}\,2\theta = \frac{{1 - {\text{ta}}{{\text{n}}^2}\,\theta }}{{2\,{\text{tan}}\,\theta }}$ .

[1]

Verify that $x = {\text{tan}}\,\theta$ and $x = - \,{\text{cot}}\,\theta$ satisfy the equation ${x^2} + \left( {2\,{\text{cot}}\,2\theta } \right)x - 1 = 0$ .

[7]

Hence, or otherwise, show that the exact value of ${\text{tan}}\frac{\pi }{{12}} = 2 - \sqrt 3$ .

[5]

Using the results from parts (b) and (c) find the exact value of ${\text{tan}}\frac{\pi }{{24}} - {\text{cot}}\frac{\pi }{{24}}$ .

Give your answer in the form $a + b\sqrt 3$ where $a$ , $b \in \mathbb{Z}$ .

[6]

Markscheme

stating the relationship between $\cot$ and $\tan$ and stating the identity for ${\text{tan}}\,2\theta$ M1

${\text{cot}}\,2\theta = \frac{1}{{{\text{tan}}\,2\theta }}$ and ${\text{tan}}\,2\theta = \frac{{2\,{\text{tan}}\,\theta }}{{1 - {\text{ta}}{{\text{n}}^2}\,\theta }}$

⇒ ${\text{cot}}\,2\theta = \frac{{1 - {\text{ta}}{{\text{n}}^2}\,\theta }}{{2\,{\text{tan}}\,\theta }}$ AG

[1 mark]

METHOD 1

attempting to substitute ${\text{tan}}\,\theta$ for $x$ and using the result from (a) M1

LHS = ${\text{ta}}{{\text{n}}^2}\,\theta + 2\,{\text{tan}}\,\theta \left( {\frac{{1 - {\text{ta}}{{\text{n}}^2}\,\theta }}{{2\,{\text{tan}}\,\theta }}} \right) - 1$ A1

${\text{ta}}{{\text{n}}^2}\,\theta + 1 - {\text{ta}}{{\text{n}}^2}\,\theta - 1 = 0$ (= RHS) A1

so $x = {\text{tan}}\,\theta$ satisfies the equation AG

attempting to substitute $- \,{\text{cot}}\,\theta$ for $x$ and using the result from (a) M1

LHS = ${\text{co}}{{\text{t}}^2}\,\theta - 2\,{\text{cot}}\,\theta \left( {\frac{{1 - {\text{ta}}{{\text{n}}^2}\,\theta }}{{2\,{\text{tan}}\,\theta }}} \right) - 1$ A1

$= \frac{1}{{{\text{ta}}{{\text{n}}^2}\,\theta }} - \left( {\frac{{1 - {\text{ta}}{{\text{n}}^2}\,\theta }}{{\,{\text{ta}}{{\text{n}}^2}\,\theta }}} \right) - 1$ A1

$\frac{1}{{{\text{ta}}{{\text{n}}^2}\,\theta }} - \frac{1}{{{\text{ta}}{{\text{n}}^2}\,\theta }} + 1 - 1 = 0$ (= RHS) A1

so $x = - \,{\text{cot}}\,\theta$ satisfies the equation AG

METHOD 2

let $\alpha = {\text{tan}}\,\theta$ and $\beta = - \,{\text{cot}}\,\theta$

attempting to find the sum of roots M1

$\alpha + \beta = {\text{tan}}\,\theta - \frac{1}{{{\text{tan}}\,\theta }}$

$= \frac{{{\text{ta}}{{\text{n}}^2}\,\theta - 1}}{{{\text{tan}}\,\theta }}$ A1

$= - 2\,{\text{cot}}\,2\theta$ (from part (a)) A1

attempting to find the product of roots M1

$\alpha \beta = {\text{tan}}\,\theta \times \left( { - \,{\text{cot}}\,\theta } \right)$ A1

= −1 A1

the coefficient of $x$ and the constant term in the quadratic are ${2\,{\text{cot}}\,2\theta }$ and −1 respectively R1

hence the two roots are $\alpha = {\text{tan}}\,\theta$ and $\beta = - \,{\text{cot}}\,\theta$ AG

[7 marks]

METHOD 1

$x = {\text{tan}}\frac{\pi }{{12}}$ and $x = - {\text{cot}}\frac{\pi }{{12}}$ are roots of ${x^2} + \left( {2\,{\text{cot}}\frac{\pi }{{6}}} \right)x - 1 = 0$ R1

Note: Award R1 if only $x = {\text{tan}}\frac{\pi }{{12}}$ is stated as a root of ${x^2} + \left( {2\,{\text{cot}}\frac{\pi }{{6}}} \right)x - 1 = 0$ .

${x^2} + 2\sqrt 3 x - 1 = 0$ A1

attempting to solve their quadratic equation M1

$x = - \sqrt 3 \pm 2$ A1

${\text{tan}}\frac{\pi }{{12}} > 0$ ( $- {\text{cot}}\frac{\pi }{{12}} < 0$ ) R1

so ${\text{tan}}\frac{\pi }{{12}} = 2 - \sqrt 3$ AG

METHOD 2

attempting to substitute $\theta = \frac{\pi }{{12}}$ into the identity for ${\text{tan}}\,2\theta$ M1

${\text{tan}}\frac{\pi }{6} = \frac{{2\,{\text{tan}}\frac{\pi }{{12}}}}{{1 - {\text{ta}}{{\text{n}}^2}\frac{\pi }{{12}}}}$

${\text{ta}}{{\text{n}}^2}\frac{\pi }{{12}} + 2\sqrt 3 \,{\text{tan}}\frac{\pi }{{12}} - 1 = 0$ A1

attempting to solve their quadratic equation M1

${\text{tan}}\frac{\pi }{{12}} = - \sqrt 3 \pm 2$ A1

${\text{tan}}\frac{\pi }{{12}} > 0$ R1

so ${\text{tan}}\frac{\pi }{{12}} = 2 - \sqrt 3$ AG

[5 marks]

${\text{tan}}\frac{\pi }{{24}} - {\text{cot}}\frac{\pi }{{24}}$ is the sum of the roots of ${x^2} + \left( {2\,{\text{cot}}\frac{\pi }{{12}}} \right)x - 1 = 0$ R1

${\text{tan}}\frac{\pi }{{24}} - {\text{cot}}\frac{\pi }{{24}} = - 2\,{\text{cot}}\frac{\pi }{{12}}$ A1

$= \frac{{ - 2}}{{2 - \sqrt 3 }}$ A1

attempting to rationalise their denominator (M1)

$= - 4 - 2\sqrt 3$ A1A1

[6 marks]

Examiners report

[N/A]

A continuous random variable $X$ has a probability density function given by

$f (x) = \{\begin{matrix} arccos x & 0 \leq x \leq 1 \\ 0 & otherwise \end{matrix}$

The median of this distribution is $m$ .

Determine the value of $m$ .

[2]

Given that $P (|X - m| \leq a) = 0.3$ , determine the value of $a$ .

[4]

Markscheme

recognises that $\int_{0}^{m} arccos x d x = 0.5$ (M1)

$m arccos m - \sqrt{1 - m^{2}} - (0 - \sqrt{1}) = 0.5$

$m = 0.360034 \dots$

$m = 0.360$ A1

[2 marks]

METHOD 1

attempts to find at least one endpoint (limit) both in terms of $m$ (or their $m$ ) and $a$ (M1)

$P (m - a \leq X \leq m + a) = 0.3$

$\int_{0.360034 \dots - a}^{0.360034 \dots + a} arccos x d x = 0.3$ (A1)

Note: Award (A1) for $\int_{m - a}^{m + a} arccos x d x = 0.3$ .

${[x arccos x - \sqrt{1 - x^{2}}]}_{0.360034 \dots - a}^{0.360034 \dots + a}$

attempts to solve their equation for $a$ (M1)

Note: The above (M1) is dependent on the first (M1).

$a = 0.124861 \dots$

$a = 0.125$ A1

METHOD 2

$\int_{- a}^{a} arccos x - 0.360034 \dots d x (= 0.3)$ (M1)(A1)

Note: Only award (M1) if at least one limit has been translated correctly.

Note: Award (M1)(A1) for $\int_{- a}^{a} arccos x - m d x (= 0.3)$ .

attempts to solve their equation for $a$ (M1)

$a = 0.124861 \dots$

$a = 0.125$ A1

METHOD 3

EITHER

$\int_{- a}^{a} arccos (x + 0.360034 \dots) d x (= 0.3)$ (M1)(A1)

Note: Only award (M1) if at least one limit has been translated correctly.

Note: Award (M1)(A1) for $\int_{- a}^{a} arccos (x + m) d x (= 0.3)$ .

$\int_{2 (0.360034 \dots) - a}^{2 (0.360034 \dots) + a} arccos (x - 0.360034 \dots) d x (= 0.3)$ (M1)(A1)

Note: Only award (M1) if at least one limit has been translated correctly.

Note: Award (M1)(A1) for $\int_{2 m - a}^{2 m + a} arccos (x - m) d x (= 0.3)$ .

THEN

attempts to solve their equation for $a$ (M1)

Note: The above (M1) is dependent on the first (M1).

$a = 0.124861 \dots$

$a = 0.125$ A1

[4 marks]

Examiners report

[N/A]

The height of water, in metres, in Dungeness harbour is modelled by the function $H (t) = a \sin (b (t - c)) + d$ , where $t$ is the number of hours after midnight, and $a, b, c$ and $d$ are constants, where $a > 0, b > 0$ and $c > 0$ .

The following graph shows the height of the water for $13$ hours, starting at midnight.

The first high tide occurs at $04 : 30$ and the next high tide occurs $12$ hours later. Throughout the day, the height of the water fluctuates between $2.2 m$ and $6.8 m$ .

All heights are given correct to one decimal place.

Show that $b = \frac{π}{6}$ .

[1]

Find the value of $a$ .

[2]

Find the value of $d$ .

[2]

Find the smallest possible value of $c$ .

[3]

Find the height of the water at $12 : 00$ .

[2]

Determine the number of hours, over a 24-hour period, for which the tide is higher than $5$ metres.

[3]

A fisherman notes that the water height at nearby Folkestone harbour follows the same sinusoidal pattern as that of Dungeness harbour, with the exception that high tides (and low tides) occur $50$ minutes earlier than at Dungeness.

Find a suitable equation that may be used to model the tidal height of water at Folkestone harbour.

[2]

Markscheme

$12 = \frac{2 π}{b}$ OR $b = \frac{2 π}{12}$ A1

$b = \frac{π}{6}$ AG

[1 mark]

$a = \frac{6.8 - 2.2}{2}$ OR $a = \frac{max - min}{2}$ (M1)

$= 2.3 (m)$ A1

[2 marks]

$d = \frac{6.8 + 2.2}{2}$ OR $d = \frac{max + min}{2}$ (M1)

$= 4.5 (m)$ A1

[2 marks]

METHOD 1

substituting $t = 4.5$ and $H = 6.8$ for example into their equation for $H$ (A1)

$6.8 = 2.3 \sin (\frac{π}{6} (4.5 - c)) + 4.5$

attempt to solve their equation (M1)

$c = 1.5$ A1

METHOD 2

using horizontal translation of $\frac{12}{4}$ (M1)

$4.5 - c = 3$ (A1)

$c = 1.5$ A1

METHOD 3

$H' (t) = (2.3) (\frac{π}{6}) \cos (\frac{π}{6} (t - c))$ (A1)

attempts to solve their $H' (4.5) = 0$ for $c$ (M1)

$(2.3) (\frac{π}{6}) \cos (\frac{π}{6} (4.5 - c)) = 0$

$c = 1.5$ A1

[3 marks]

attempt to find $H$ when $t = 12$ or $t = 0$ , graphically or algebraically (M1)

$H = 2.87365 \dots$

$H = 2.87 (m)$ A1

[2 marks]

attempt to solve $5 = 2.3 \sin (\frac{π}{6} (t - 1.5)) + 4.5$ (M1)

times are $t = 1.91852 \dots$ and $t = 7.08147 \dots, (t = 13.9185 \dots, t = 19.0814 \dots)$ (A1)

total time is $2 \times (7.081 \dots - 1.919 \dots)$

$10.3258 \dots$

$= 10.3$ (hours) A1

Note: Accept $10$ .

[3 marks]

METHOD 1

substitutes $t = \frac{11}{3}$ and $H = 6.8$ into their equation for $H$ and attempts to solve for $c$ (M1)

$6.8 = 2.3 \sin (\frac{π}{6} (\frac{11}{3} - c)) + 4.5 \Rightarrow c = \frac{2}{3}$

$H (t) = 2.3 \sin (\frac{π}{6} (t - \frac{2}{3})) + 4.5$ A1

METHOD 2
uses their horizontal translation $(\frac{12}{4} = 3)$ (M1)

$\frac{11}{3} - c = 3 \Rightarrow c = \frac{2}{3}$

$H (t) = 2.3 \sin (\frac{π}{6} (t - \frac{2}{3})) + 4.5$ A1

[2 marks]

Examiners report

[N/A]

The voltage $v$ in a circuit is given by the equation

$v\left( t \right) = 3\,{\text{sin}}\left( {100\pi t} \right)$ , $t \geqslant 0$ where $t$ is measured in seconds.

The current $i$ in this circuit is given by the equation

$i\left( t \right) = 2\,{\text{sin}}\left( {100\pi \left( {t + 0.003} \right)} \right)$ .

The power $p$ in this circuit is given by $p\left( t \right) = v\left( t \right) \times i\left( t \right)$ .

The average power ${p_{av}}$ in this circuit from $t = 0$ to $t = T$ is given by the equation

${p_{av}}\left( T \right) = \frac{1}{T}\int_0^T {p\left( t \right){\text{d}}t}$ , where $T > 0$ .

Write down the maximum and minimum value of $v$ .

[2]

Write down two transformations that will transform the graph of $y = v\left( t \right)$ onto the graph of $y = i\left( t \right)$ .

[2]

Sketch the graph of $y = p\left( t \right)$ for 0 ≤ $t$ ≤ 0.02 , showing clearly the coordinates of the first maximum and the first minimum.

[3]

Find the total time in the interval 0 ≤ $t$ ≤ 0.02 for which $p\left( t \right)$ ≥ 3.

[3]

Find ${p_{av}}$ (0.007).

[2]

With reference to your graph of $y = p\left( t \right)$ explain why ${p_{av}}\left( T \right)$ > 0 for all $T$ > 0.

[2]

Given that $p\left( t \right)$ can be written as $p\left( t \right) = a\,{\text{sin}}\left( {b\left( {t - c} \right)} \right) + d$ where $a$ , $b$ , $c$ , $d$ > 0, use your graph to find the values of $a$ , $b$ , $c$ and $d$ .

[6]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

3, −3 A1A1

[2 marks]

stretch parallel to the $y$ -axis (with $x$ -axis invariant), scale factor $\frac{2}{3}$ A1

translation of $\left( {\begin{array}{*{20}{c}} { - 0.003} \\ 0 \end{array}} \right)$ (shift to the left by 0.003) A1

Note: Can be done in either order.

[2 marks]

correct shape over correct domain with correct endpoints    A1
first maximum at (0.0035, 4.76)    A1
first minimum at (0.0085, −1.24)    A1

[3 marks]

$p$ ≥ 3 between $t$ = 0.0016762 and 0.0053238 and $t$ = 0.011676 and 0.015324 (M1)(A1)

Note: Award M1A1 for either interval.

= 0.00730 A1

[3 marks]

${p_{av}} = \frac{1}{{0.007}}\int_0^{0.007} {6\,{\text{sin}}\left( {100\pi t} \right)} {\text{sin}}\left( {100\pi \left( {t + 0.003} \right)} \right){\text{d}}t$ (M1)

= 2.87 A1

[2 marks]

in each cycle the area under the $t$ axis is smaller than area above the $t$ axis R1

the curve begins with the positive part of the cycle R1

[2 marks]

$a = \frac{{4.76 - \left( { - 1.24} \right)}}{2}$ (M1)

$a = 3.00$ A1

$d = \frac{{4.76 + \left( { - 1.24} \right)}}{2}$

$d = 1.76$ A1

$b = \frac{{2\pi }}{{0.01}}$

$b = 628\left( { = 200\pi } \right)$ A1

$c = 0.0035 - \frac{{0.01}}{4}$ (M1)

$c = 0.00100$ A1

[6 marks]

Examiners report

[N/A]

Consider the rectangle OABC such that AB = OC = 10 and BC = OA = 1 , with the points P , Q and R placed on the line OC such that OP = $p$ , OQ = $q$ and OR = $r$ , such that 0 < $p$ < $q$ < $r$ < 10.

Let ${\theta _p}$ be the angle APO, ${\theta _q}$ be the angle AQO and ${\theta _r}$ be the angle ARO.

Consider the case when ${\theta _p} = {\theta _q} + {\theta _r}$ and QR = 1.

Find an expression for ${\theta _p}$ in terms of $p$ .

[3]

Show that $p = \frac{{{q^2} + q - 1}}{{2q + 1}}$ .

[6]

By sketching the graph of $p$ as a function of $q$ , determine the range of values of $p$ for which there are possible values of $q$ .

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

use of tan (M1)

${\text{tan}}\,{\theta _p} = \frac{1}{p}$ (A1)

${\theta _p} = {\text{arctan}}\left( {\frac{1}{p}} \right)$ A1

METHOD 2

AP $= \sqrt {{p^2} + 1}$ (A1)

use of sin, cos, sine rule or cosine rule using the correct length of AP (M1)

${\theta _p} = {\text{arcsin}}\left( {\frac{1}{{\sqrt {{p^2} + 1} }}} \right)$ or ${\theta _p} = {\text{arccos}}\left( {\frac{p}{{\sqrt {{p^2} + 1} }}} \right)$ A1

[3 marks]

QR = 1 ⇒ $r = q + 1$ (A1)

Note: This may be seen anywhere.

${\text{tan}}\,{\theta _p} = {\text{tan}}\left( {{\theta _q} + {\theta _r}} \right)$

attempt to use compound angle formula for tan M1

${\text{tan}}\,{\theta _p} = \frac{{{\text{tan}}\,{\theta _q} + {\text{tan}}\,{\theta _r}}}{{1 - {\text{tan}}\,{\theta _q}\,{\text{tan}}\,{\theta _r}}}$ (A1)

$\frac{1}{p} = \frac{{\frac{1}{q} + \frac{1}{r}}}{{1 - \left( {\frac{1}{q}} \right)\left( {\frac{1}{r}} \right)}}$ (M1)

$\frac{1}{p} = \frac{{\frac{1}{q} + \frac{1}{{q + 1}}}}{{1 - \left( {\frac{1}{q}} \right)\left( {\frac{1}{{q + 1}}} \right)}}$ or $p = \frac{{1 - \left( {\frac{1}{q}} \right)\left( {\frac{1}{{q + 1}}} \right)}}{{\left( {\frac{1}{q}} \right) + \left( {\frac{1}{{q + 1}}} \right)}}$ A1

$\frac{1}{p} = \frac{{q + q + 1}}{{q\left( {q + 1} \right) - 1}}$ M1

Note: Award M1 for multiplying top and bottom by ${q\left( {q + 1} \right)}$ .

$p = \frac{{{q^2} + q - 1}}{{2q + 1}}$ AG

[6 marks]

increasing function with positive $q$ -intercept A1

Note: Accept curves which extend beyond the domain shown above.

(0.618 <) $q$ < 9 (A1)

⇒ range is (0 <) $p$ < 4.68 (A1)

0 < $p$ < 4.68 A1

[4 marks]

Examiners report

[N/A]

The plane $Π_{1}$ has equation $3 x - y + z = - 13$ and the line $L$ has vector equation

$r = (\begin{matrix} 1 \\ 2 \\ - 2 \end{matrix}) + λ (\begin{matrix} - 3 \\ - 1 \\ 4 \end{matrix}), λ \in ℝ$ .

The plane $Π_{2}$ contains the point $O$ and the line $L$ .

Given that $L$ meets $Π_{1}$ at the point $P$ , find the coordinates of $P$ .

[4]

Find the shortest distance from the point $O (0, 0, 0)$ to $Π_{1}$ .

[4]

Find the equation of $Π_{2}$ , giving your answer in the form $r . n = d$ .

[3]

Determine the acute angle between $Π_{1}$ and $Π_{2}$ .

[5]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$3 (1 - 3 λ) - (2 - λ) + (- 2 + 4 λ) = - 13$ (M1)

$λ = 3$ (A1)

$r = (\begin{matrix} 1 \\ 2 \\ - 2 \end{matrix}) + 3 (\begin{matrix} - 3 \\ - 1 \\ 4 \end{matrix}) = (\begin{matrix} 8 \\ - 1 \\ 10 \end{matrix})$ (M1)

so $P (- 8, - 1, 10)$ A1

Note: Do not award the final A1 if a vector given instead of coordinates

[4 marks]

METHOD 1

$r = μ (\begin{matrix} 3 \\ - 1 \\ 1 \end{matrix})$

substituting into equation of the plane M1

$9 μ + μ + μ = - 13$

$μ = - \frac{13}{11} (= - 1.18 \dots)$ A1

distance $= \frac{13 \sqrt{3^{2} + {(- 1)}^{2} + 1^{2}}}{11}$ (M1)

$= \frac{13}{\sqrt{11}} (= \frac{13 \sqrt{11}}{11} = 3.92)$ A1

METHOD 2

choice of any point on the plane, eg $(- 8, - 1, 10)$ to use in distance formula (M1)

so distance $= \frac{(\begin{matrix} - 8 \\ - 1 \\ 10 \end{matrix}) \cdot (\begin{matrix} - 3 \\ 1 \\ - 1 \end{matrix})}{\sqrt{{(- 3)}^{2} + 1^{2} + {(- 1)}^{2}}}$ A1A1

Note: Award A1 for numerator, A1 for denominator.

$= \frac{24 - 1 - 10}{\sqrt{11}}$

$= \frac{13}{\sqrt{11}} (= \frac{13 \sqrt{11}}{11} = 3.92)$ A1

[4 marks]

EITHER

identify two vectors (A1)

eg, $(\begin{matrix} 1 \\ 2 \\ - 2 \end{matrix})$ and $(\begin{matrix} - 3 \\ - 1 \\ 4 \end{matrix})$

$n = (\begin{matrix} 1 \\ 2 \\ - 2 \end{matrix}) \times (\begin{matrix} - 3 \\ - 1 \\ 4 \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ 5 \end{matrix})$ (M1)

identify three points in the plane (A1)

eg $λ = 0, 1$ gives $(\begin{matrix} 1 \\ 2 \\ - 2 \end{matrix})$ and $(\begin{matrix} - 2 \\ 1 \\ 2 \end{matrix})$

solving system of equations (M1)

THEN

$Π_{2} : r . (\begin{matrix} 6 \\ 2 \\ 5 \end{matrix}) = 0$ A1

Note: Accept $6 x + 2 y + 5 z = 0$ .

[3 marks]

vector normal to $Π_{1}$ is eg $n_{1} = (\begin{matrix} 3 \\ - 1 \\ 1 \end{matrix})$

vector normal to $Π_{2}$ is eg $n_{2} = (\begin{matrix} 6 \\ 2 \\ 5 \end{matrix})$ (A1)

required angle is $θ$ , where $\cos θ \frac{(\begin{matrix} 3 \\ - 1 \\ 1 \end{matrix}) \cdot (\begin{matrix} 6 \\ 2 \\ 5 \end{matrix})}{\sqrt{11} \sqrt{65}}$ M1A1

$\cos θ = \frac{21}{\sqrt{11} \sqrt{65}} = 0.785 \dots$ (A1)

$θ = 0.667526 \dots$

$θ = 0.668 (= 38.2 °)$ A1

Note: Award the penultimate (A1) but not the final A1 for the obtuse angle $2.47406 \dots$ or $142 °$ .

[5 marks]

Examiners report

[N/A]

A particle $P$ moves in a straight line such that after time $t$ seconds, its velocity, $v$ in ${m s}^{- 1}$ , is given by $v = e^{- 3 t} \sin 6 t$ , where $0 < t < \frac{π}{2}$ .

At time $t$ , $P$ has displacement $s (t)$ ; at time $t = 0$ , $s (0) = 0$ .

At successive times when the acceleration of $P$ is $0 {m s}^{- 2}$ , the velocities of $P$ form a geometric sequence. The acceleration of $P$ is zero at times $t_{1}, t_{2}, t_{3}$ where $t_{1} < t_{2} < t_{3}$ and the respective velocities are $v_{1}, v_{2}, v_{3}$ .

Find the times when $P$ comes to instantaneous rest.

[2]

Find an expression for $s$ in terms of $t$ .

[7]

Find the maximum displacement of $P$ , in metres, from its initial position.

[2]

Find the total distance travelled by $P$ in the first $1.5$ seconds of its motion.

[2]

Show that, at these times, $\tan 6 t = 2$ .

[2]

e.i.

Hence show that $\frac{v_{2}}{v_{1}} = \frac{v_{3}}{v_{2}} = - e^{- \frac{π}{2}}$ .

[5]

e.ii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{π}{6} (= 0.524)$ A1

$\frac{π}{3} (= 1.05)$ A1

[2 marks]

attempt to use integration by parts M1

$s = \int e^{- 3 t} \sin 6 t d t$

EITHER

$= - \frac{e^{- 3 t} \sin 6 t}{3} - \int - 2 e^{- 3 t} cos 6 t d t$ A1

$= - \frac{e^{- 3 t} \sin 6 t}{3} - (\frac{2 e^{- 3 t} cos 6 t}{3} - \int - 4 e^{- 3 t} sin 6 t d t)$ A1

$= - \frac{e^{- 3 t} \sin 6 t}{3} - (\frac{2 e^{- 3 t} cos 6 t}{3} + 4 s)$

$5 s = \frac{-3 e^{- 3 t} \sin 6 t - 6 e^{- 3 t} cos 6 t}{9}$ M1

$= - \frac{e^{- 3 t} cos 6 t}{6} - \int \frac{1}{2} e^{- 3 t} cos 6 t d t$ A1

$= - \frac{e^{- 3 t} cos 6 t}{6} - (\frac{e^{- 3 t} sin 6 t}{12} + \int \frac{1}{4} e^{- 3 t} sin 6 t d t)$ A1

$= - \frac{e^{- 3 t} cos 6 t}{6} - (\frac{e^{- 3 t} sin 6 t}{12} + \frac{1}{4} s)$

$\frac{5}{4} s = \frac{- 2 e^{- 3 t} cos 6 t - e^{- 3 t} sin 6 t}{12}$ M1

THEN

$s = - \frac{e^{- 3 t} (sin 6 t + 2 cos 6 t)}{15} (+ c)$ A1

at $t = 0, s = 0 \Rightarrow 0 = - \frac{2}{15} + c$ M1

$c = \frac{2}{15}$ A1

$s = \frac{2}{15} - \frac{e^{- 3 t} (sin 6 t + 2 cos 6 t)}{15}$

[7 marks]

EITHER

substituting $t = \frac{π}{6}$ into their equation for $s$ (M1)

$(s = \frac{2}{15} - \frac{e^{- \frac{π}{2}} (sin π + 2 cos π)}{15})$

using GDC to find maximum value (M1)

evaluating $\int_{0}^{\frac{π}{6}} v d t$ (M1)

THEN

$= 0.161 (= \frac{2}{15} (1 + e^{- \frac{π}{2}}))$ A1

[2 marks]

METHOD 1

EITHER

distance required $= \int_{0}^{1.5} |e^{- 3 t} \sin 6 t| d t$ (M1)

distance required $= \int_{0}^{\frac{π}{6}} e^{- 3 t} \sin 6 t d t + |\int_{\frac{π}{6}}^{\frac{π}{3}} e^{- 3 t} \sin 6 t d t| + \int_{\frac{π}{3}}^{1.5} e^{- 3 t} \sin 6 t d t$ (M1)

$(= 0.16105 \dots + 0.033479 \dots + 0.006806 \dots)$

THEN

$= 0.201 (m)$ A1

METHOD 2

using successive minimum and maximum values on the displacement graph (M1)

$0.16105 \dots + (0.16105 \dots - 0.12757 \dots) + (0.13453 \dots - 0.12757 \dots)$

$= 0.201 (m)$ A1

[2 marks]

valid attempt to find $\frac{d v}{d t}$ using product rule and set $\frac{d v}{d t} = 0$ M1

$\frac{d v}{d t} = e^{- 3 t} 6 \cos 6 t - 3 e^{- 3 t} \sin 6 t$ A1

$\frac{d v}{d t} = 0 \Rightarrow \tan 6 t = 2$ AG

[2 marks]

e.i.

attempt to evaluate $t_{1}, t_{2}, t_{3}$ in exact form M1

$6 t_{1} = arctan 2 (\Rightarrow t_{1} = \frac{1}{6} arctan 2)$

$6 t_{2} = π + arctan 2 (\Rightarrow t_{2} = \frac{π}{6} + \frac{1}{6} arctan 2)$

$6 t_{3} = 2 π + arctan 2 (\Rightarrow t_{3} = \frac{π}{3} + \frac{1}{6} arctan 2)$ A1

Note: The A1 is for any two consecutive correct, or showing that $6 t_{2} = π + 6 t_{1}$ or $6 t_{3} = π + 6 t_{2}$ .

showing that $\sin 6 t_{n + 1} = - \sin 6 t_{n}$

eg $\tan 6 t = 2 \Rightarrow \sin 6 t = \pm \frac{2}{\sqrt{5}}$ M1A1

showing that $\frac{e^{- 3 t_{n +1}}}{e^{- 3 t_{n}}} = e^{- \frac{π}{2}}$ M1

eg $e^{- 3 (\frac{π}{6} + k)} \div e^{- 3 k} = e^{- \frac{π}{2}}$

Note: Award the A1 for any two consecutive terms.

$\frac{v_{3}}{v_{2}} = \frac{v_{2}}{v_{1}} = - e^{- \frac{π}{2}}$ AG

[5 marks]

e.ii.

Examiners report

[N/A]

e.i.

[N/A]

e.ii.

Find the set of values of $k$ that satisfy the inequality ${k^2} - k - 12 < 0$ .

[2]

The triangle ABC is shown in the following diagram. Given that $\cos B < \frac{1}{4}$ , find the range of possible values for AB.

M17/5/MATHL/HP2/ENG/TZ2/04.b

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

${k^2} - k - 12 < 0$

$(k - 4)(k + 3) < 0$ (M1)

$- 3 < k < 4$ A1

[2 marks]

$\cos B = \frac{{{2^2} + {c^2} - {4^2}}}{{4c}}{\text{ }}({\text{or }}16 = {2^2} + {c^2} - 4c\cos B)$ M1

$\Rightarrow \frac{{{c^2} - 12}}{{4c}} < \frac{1}{4}$ A1

$\Rightarrow {c^2} - c - 12 < 0$

from result in (a)

$0 < {\text{AB}} < 4$ or $- 3 < {\text{AB}} < 4$ (A1)

but AB must be at least 2

$\Rightarrow 2 < {\text{AB}} < 4$ A1

Note: Allow $\leqslant {\text{AB}}$ for either of the final two A marks.

[4 marks]

Examiners report

[N/A]

Two airplanes, $A$ and $B$ , have position vectors with respect to an origin $O$ given respectively by

$r_{A} = (\begin{matrix} 19 \\ - 1 \\ 1 \end{matrix}) + t (\begin{matrix} - 6 \\ 2 \\ 4 \end{matrix})$

$r_{B} = (\begin{matrix} 1 \\ 0 \\ 12 \end{matrix}) + t (\begin{matrix} 4 \\ 2 \\ - 2 \end{matrix})$

where $t$ represents the time in minutes and $0 \leq t \leq 2.5$ .

Entries in each column vector give the displacement east of $O$ , the displacement north of $O$ and the distance above sea level, all measured in kilometres.

The two airplanes’ lines of flight cross at point $P$ .

Find the three-figure bearing on which airplane $B$ is travelling.

[2]

Show that airplane $A$ travels at a greater speed than airplane $B$ .

[2]

Find the acute angle between the two airplanes’ lines of flight. Give your answer in degrees.

[4]

Find the coordinates of $P$ .

[5]

d.i.

Determine the length of time between the first airplane arriving at $P$ and the second airplane arriving at $P$ .

[2]

d.ii.

Let $D (t)$ represent the distance between airplane $A$ and airplane $B$ for $0 \leq t \leq 2.5$ .

Find the minimum value of $D (t)$ .

[5]

Markscheme

let $ϕ$ be the required angle (bearing)

EITHER

$ϕ = 90 ° - arctan \frac{1}{2} (= arctan 2)$ (M1)

Note: Award M1 for a labelled sketch.

$\cos ϕ = \frac{(\begin{matrix} 0 \\ 1 \end{matrix}) \cdot (\begin{matrix} 4 \\ 2 \end{matrix})}{\sqrt{1} \times \sqrt{20}} (= 0.4472 \dots, = \frac{1}{\sqrt{5}})$ (M1)

$ϕ = arccos (0.4472 \dots)$

THEN

$063 °$ A1

Note: Do not accept $063.6 °$ or $63.4 °$ or $1 . 10^{c}$ .

[2 marks]

METHOD 1

let $|b_{A}|$ be the speed of $A$ and let $|b_{B}|$ be the speed of $B$

attempts to find the speed of one of $A$ or $B$ (M1)

$|b_{A}| = \sqrt{{(- 6)}^{2} + 2^{2} + 4^{2}}$ or $|b_{B}| = \sqrt{4^{2} + 2^{2} + {(- 2)}^{2}}$

Note: Award M0 for $|b_{A}| = \sqrt{19^{2} + {(- 1)}^{2} + 1^{2}}$ and $|b_{B}| = \sqrt{1^{2} + 0^{2} + 12^{2}}$ .

$|b_{A}| = 7.48 \dots (= \sqrt{56})$ (km min^-1) and $|b_{B}| = 4.89 \dots (= \sqrt{24})$ (km min^-1) A1

$|b_{A}| > |b_{B}|$ so $A$ travels at a greater speed than $B$ AG

METHOD 2

attempts to use $speed = \frac{distance}{time}$

${speed}_{A} = \frac{|r_{A} (t_{2}) - r_{A} (t_{1})|}{t_{2} - t_{1}}$ and ${speed}_{B} = \frac{|r_{B} (t_{2}) - r_{B} (t_{1})|}{t_{2} - t_{1}}$ (M1)

for example:

${speed}_{A} = \frac{|r_{A} (1) - r_{A} (0)|}{1}$ and ${speed}_{B} = \frac{|r_{B} (1) - r_{B} (0)|}{1}$

${speed}_{A} = \frac{\sqrt{{(- 6)}^{2} + 2^{2} + 4^{2}}}{1}$ and ${speed}_{B} = \frac{\sqrt{4^{2} + 2^{2} + 2^{2}}}{1}$

${speed}_{A} = 7.48 \dots (2 \sqrt{14})$ and ${speed}_{B} = 4.89 \dots (\sqrt{24})$ A1

${speed}_{A} > {speed}_{B}$ so $A$ travels at a greater speed than $B$ AG

[2 marks]

attempts to use the angle between two direction vectors formula (M1)

$\cos θ = \frac{(- 6) (4) + (2) (2) + (4) (- 2)}{\sqrt{{(- 6)}^{2} + 2^{2} + 4^{2}} \sqrt{4^{2} + 2^{2} + {(- 2)}^{2}}}$ (A1)

$\cos θ = - 0.7637 \dots (= - \frac{7}{\sqrt{84}})$ or $θ = arccos (- 0.7637 \dots) (= 2.4399 \dots)$

attempts to find the acute angle $180 ° - θ$ using their value of $θ$ (M1)

$= 40.2 °$ A1

[4 marks]

for example, sets $r_{A} (t_{1}) = r_{B} (t_{2})$ and forms at least two equations (M1)

$19 - 6 t_{1} = 1 + 4 t_{2}$

$- 1 + 2 t_{1} = 2 t_{2}$

$1 + 4 t_{1} = 12 - 2 t_{2}$

Note: Award M0 for equations involving $t$ only.

EITHER

attempts to solve the system of equations for one of $t_{1}$ or $t_{2}$ (M1)

$t_{1} = 2$ or $t_{2} = \frac{3}{2}$ A1

attempts to solve the system of equations for $t_{1}$ and $t_{2}$ (M1)

$t_{1} = 2$ or $t_{2} = \frac{3}{2}$ A1

THEN

substitutes their $t_{1}$ or $t_{2}$ value into the corresponding $r_{A}$ or $r_{B}$ (M1)

$P (7, 3, 9)$ A1

Note: Accept $\vec{OP} = (\begin{matrix} 7 \\ 3 \\ 9 \end{matrix})$ . Accept $7$ km east of $O$ , $3$ km north of $O$ and $9$ km above sea level.

[5 marks]

d.i.

attempts to find the value of $t_{1} - t_{2}$ (M1)

$t_{1} - t_{2} = 2 - \frac{3}{2}$

$0.5$ minutes ( $30$ seconds) A1

[2 marks]

d.ii.

EITHER

attempts to find $r_{B} - r_{A}$ (M1)

$r_{B} - r_{A} = (\begin{matrix} - 18 \\ 1 \\ 11 \end{matrix}) + t (\begin{matrix} 10 \\ 0 \\ - 6 \end{matrix})$

attempts to find their $D (t)$ (M1)

$D (t) = \sqrt{{(10 t - 18)}^{2} + 1 + {(11 - 6 t)}^{2}}$ A1

attempts to find $r_{A} - r_{B}$ (M1)

$r_{A} - r_{B} = (\begin{matrix} 18 \\ - 1 \\ - 11 \end{matrix}) + t (\begin{matrix} - 10 \\ 0 \\ 6 \end{matrix})$

attempts to find their $D (t)$ (M1)

$D (t) = \sqrt{{(18 - 10 t)}^{2} + {(- 1)}^{2} + {(- 11 + 6 t)}^{2}}$ A1

Note: Award M0M0A0 for expressions using two different time parameters.

THEN

either attempts to find the local minimum point of $D (t)$ or attempts to find the value of $t$ such that $D' (t) = 0$ (or equivalent) (M1)

$t = 1.8088 \dots (= \frac{123}{68})$

$D (t) = 1.01459 \dots$

minimum value of $D (t)$ is $1.01 (= \frac{\sqrt{1190}}{34})$ (km) A1

Note: Award M0 for attempts at the shortest distance between two lines.

[5 marks]

Examiners report

General comment about this question: many candidates were not exposed to this setting of vectors question and were rather lost.

Part (a) Probably the least answered question on the whole paper. Many candidates left it blank, others tried using 3D vectors. Out of those who calculated the angle correctly, only a small percentage were able to provide the correct true bearing as a 3-digit figure.

Part (b) Well done by many candidates who used the direction vectors to calculate and compare the speeds. A number of candidates tried to use the average rate of change but mostly unsuccessfully.

Part (c) Most candidates used the correct vectors and the formula to obtain the obtuse angle. Then only some read the question properly to give the acute angle in degrees, as requested.

Part (d) Well done by many candidates who used two different parameters. They were able to solve and obtain two values for time, the difference in minutes and the correct point of intersection. A number of candidates only had one parameter, thus scoring no marks in part (d) (i). The frequent error in part (d)(ii) was providing incorrect units.

Part (e) Many correct answers were seen with an efficient way of setting the question and using their GDC to obtain the answer, graphically or numerically. Some gave time only instead of actually giving the minimal distance. A number of candidates tried to find the distance between two skew lines ignoring the fact that the lines intersect.

[N/A]

d.i.

[N/A]

d.ii.

[N/A]

A water trough which is 10 metres long has a uniform cross-section in the shape of a semicircle with radius 0.5 metres. It is partly filled with water as shown in the following diagram of the cross-section. The centre of the circle is O and the angle KOL is $\theta$ radians.

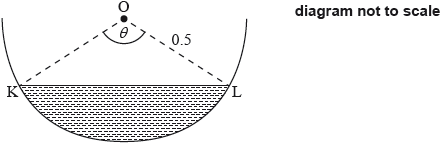
M17/5/MATHL/HP2/ENG/TZ1/08

The volume of water is increasing at a constant rate of $0.0008{\text{ }}{{\text{m}}^3}{{\text{s}}^{ - 1}}$ .

Find an expression for the volume of water $V{\text{ }}({{\text{m}}^3})$ in the trough in terms of $\theta$ .

[3]

Calculate $\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ when $\theta = \frac{\pi }{3}$ .

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

area of segment $= \frac{1}{2} \times {0.5^2} \times (\theta - \sin \theta )$ M1A1

$V = {\text{area of segment}} \times 10$

$V = \frac{5}{4}(\theta - \sin \theta )$ A1

[3 marks]

METHOD 1

$\frac{{{\text{d}}V}}{{{\text{d}}t}} = \frac{5}{4}(1 - \cos \theta )\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ M1A1

$0.0008 = \frac{5}{4}\left( {1 - \cos \frac{\pi }{3}} \right)\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ (M1)

$\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.00128{\text{ }}({\text{rad}}\,{s^{ - 1}})$ A1

METHOD 2

$\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{{\text{d}}\theta }}{{{\text{d}}V}} \times \frac{{{\text{d}}V}}{{{\text{d}}t}}$ (M1)

$\frac{{{\text{d}}V}}{{{\text{d}}\theta }} = \frac{5}{4}(1 - \cos \theta )$ A1

$\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{4 \times 0.0008}}{{5\left( {1 - \cos \frac{\pi }{3}} \right)}}$ (M1)

$\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.00128\left( {\frac{4}{{3125}}} \right)({\text{rad }}{s^{ - 1}})$ A1

[4 marks]

Examiners report

[N/A]

Consider the function $f$ defined by $f(x) = 3x\arccos (x)$ where $- 1 \leqslant x \leqslant 1$ .

Sketch the graph of $f$ indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.

[3]

State the range of $f$ .

[2]

Solve the inequality $\left| {3x\arccos (x)} \right| > 1$ .

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

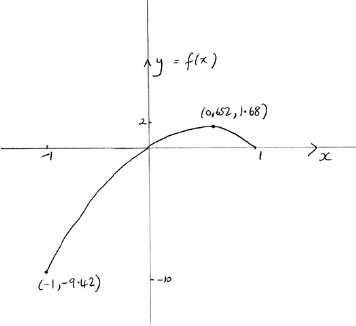
N16/5/MATHL/HP2/ENG/TZ0/05.a/M

correct shape passing through the origin and correct domain A1

Note: Endpoint coordinates are not required. The domain can be indicated by $- 1$ and 1 marked on the axis.

$(0.652,{\text{ }}1.68)$ A1

two correct intercepts (coordinates not required) A1

Note: A graph passing through the origin is sufficient for $(0,{\text{ }}0)$ .

[3 marks]

$[-9.42,{\text{ }}1.68]{\text{ }}({\text{or }} - 3\pi ,{\text{ }}1.68])$ A1A1

Note: Award A1A0 for open or semi-open intervals with correct endpoints. Award A1A0 for closed intervals with one correct endpoint.

[2 marks]

attempting to solve either $\left| {3x\arccos (x)} \right| > 1$ (or equivalent) or $\left| {3x\arccos (x)} \right| = 1$ (or equivalent) (eg. graphically) (M1)

N16/5/MATHL/HP2/ENG/TZ0/05.c/M

$x = - 0.189,{\text{ }}0.254,{\text{ }}0.937$ (A1)

$- 1 \leqslant x < - 0.189{\text{ or }}0.254 < x < 0.937$ A1A1

Note: Award A0 for $x < - 0.189$ .

[4 marks]

Examiners report

[N/A]

Consider the function $f(x) = 2{\sin ^2}x + 7\sin 2x + \tan x - 9,{\text{ }}0 \leqslant x < \frac{\pi }{2}$ .

Let $u = \tan x$ .

Determine an expression for $f’(x)$ in terms of $x$ .

[2]

a.i.

Sketch a graph of $y = f’(x)$ for $0 \leqslant x < \frac{\pi }{2}$ .

[4]

a.ii.

Find the $x$ -coordinate(s) of the point(s) of inflexion of the graph of $y = f(x)$ , labelling these clearly on the graph of $y = f’(x)$ .

[2]

a.iii.

Express $\sin x$ in terms of $\mu$ .

[2]

b.i.

Express $\sin 2x$ in terms of $u$ .

[3]

b.ii.

Hence show that $f(x) = 0$ can be expressed as ${u^3} - 7{u^2} + 15u - 9 = 0$ .

[2]

b.iii.

Solve the equation $f(x) = 0$ , giving your answers in the form $\arctan k$ where $k \in \mathbb{Z}$ .

[3]

Markscheme

$f’(x) = 4\sin x\cos x + 14\cos 2x + {\sec ^2}x$ (or equivalent) (M1)A1

[2 marks]

a.i.

N17/5/MATHL/HP2/ENG/TZ0/11.a.ii/M A1A1A1A1

Note: Award A1 for correct behaviour at $x = 0$ , A1 for correct domain and correct behaviour for $x \to \frac{\pi }{2}$ , A1 for two clear intersections with $x$ -axis and minimum point, A1 for clear maximum point.

[4 marks]

a.ii.

$x = 0.0736$ A1

$x = 1.13$ A1

[2 marks]

a.iii.

attempt to write $\sin x$ in terms of $u$ only (M1)

$\sin x = \frac{u}{{\sqrt {1 + {u^2}} }}$ A1

[2 marks]

b.i.

$\cos x = \frac{1}{{\sqrt {1 + {u^2}} }}$ (A1)

attempt to use $\sin 2x = 2\sin x\cos x{\text{ }}\left( { = 2\frac{u}{{\sqrt {1 + {u^2}} }}\frac{1}{{\sqrt {1 + {u^2}} }}} \right)$ (M1)

$\sin 2x = \frac{{2u}}{{1 + {u^2}}}$ A1

[3 marks]

b.ii.

$2{\sin ^2}x + 7\sin 2x + \tan x - 9 = 0$

$\frac{{2{u^2}}}{{1 + {u^2}}} + \frac{{14u}}{{1 + {u^2}}} + u - 9{\text{ }}( = 0)$ M1

$\frac{{2{u^2} + 14u + u(1 + {u^2}) - 9(1 + {u^2})}}{{1 + {u^2}}} = 0$ (or equivalent) A1

${u^3} - 7{u^2} + 15u - 9 = 0$ AG

[2 marks]

b.iii.

$u = 1$ or $u = 3$ (M1)

$x = \arctan (1)$ A1

$x = \arctan (3)$ A1

Note: Only accept answers given the required form.

[3 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

a.iii.

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

b.iii.

[N/A]

Two submarines A and B have their routes planned so that their positions at time t hours, 0 ≤ t < 20 , would be defined by the position vectors r_A $= \left( \begin{gathered} \,2 \hfill \\ \,4 \hfill \\ - 1 \hfill \\ \end{gathered} \right) + t\left( \begin{gathered} - 1 \hfill \\ \,1 \hfill \\ - 0.15 \hfill \\ \end{gathered} \right)$ and r_B $= \left( \begin{gathered} \,0 \hfill \\ \,3.2 \hfill \\ - 2 \hfill \\ \end{gathered} \right) + t\left( \begin{gathered} - 0.5 \hfill \\ \,1.2 \hfill \\ \,0.1 \hfill \\ \end{gathered} \right)$ relative to a fixed point on the surface of the ocean (all lengths are in kilometres).

To avoid the collision submarine B adjusts its velocity so that its position vector is now given by

r_B $= \left( \begin{gathered} \,0 \hfill \\ \,3.2 \hfill \\ - 2 \hfill \\ \end{gathered} \right) + t\left( \begin{gathered} - 0.45 \hfill \\ \,1.08 \hfill \\ \,0.09 \hfill \\ \end{gathered} \right)$ .

Show that the two submarines would collide at a point P and write down the coordinates of P.

[4]

Show that submarine B travels in the same direction as originally planned.

[1]

b.i.

Find the value of t when submarine B passes through P.

[2]

b.ii.

Find an expression for the distance between the two submarines in terms of t.

[5]

c.i.

Find the value of t when the two submarines are closest together.

[2]

c.ii.

Find the distance between the two submarines at this time.

[1]

c.iii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

r_A= r_{B (M1)}

2 − t = − 0.5t ⇒ t = 4 A1

checking t = 4 satisfies 4 + t = 3.2 + 1.2t and − 1 − 0.15t = − 2 + 0.1t R1

P(−2, 8, −1.6) A1

Note: Do not award final A1 if answer given as column vector.

[4 marks]

$0.9 \times \left( \begin{gathered} - 0.5 \hfill \\ \,1.2 \hfill \\ \,0.1 \hfill \\ \end{gathered} \right) = \left( \begin{gathered} - 0.45 \hfill \\ \,1.08 \hfill \\ \,0.09 \hfill \\ \end{gathered} \right)$ A1

Note: Accept use of cross product equalling zero.

hence in the same direction AG

[1 mark]

b.i.

$\left( \begin{gathered} \, - 0.45t \hfill \\ 3.2 + 1.08t \hfill \\ - 2 + 0.09t \hfill \\ \end{gathered} \right) = \left( \begin{gathered} - 2 \hfill \\ \,8 \hfill \\ - 1.6 \hfill \\ \end{gathered} \right)$ M1

Note: The M1 can be awarded for any one of the resultant equations.

$\Rightarrow t = \frac{{40}}{9} = 4.44 \ldots$ A1

[2 marks]

b.ii.

r_A − r_B = $\left( \begin{gathered} \,2 - t \hfill \\ \,4 + t \hfill \\ - 1 - 0.15t \hfill \\ \end{gathered} \right) - \left( \begin{gathered} \, - 0.45t \hfill \\ 3.2 + 1.08t \hfill \\ - 2 + 0.09t \hfill \\ \end{gathered} \right)$ (M1)(A1)

$= \left( \begin{gathered} \,2 - 0.55t \hfill \\ \,0.8 - 0.08t \hfill \\ 1 - 0.24t \hfill \\ \end{gathered} \right)$ (A1)

Note: Accept r_A − r_B.

distance $D = \sqrt {{{\left( {2 - 0.55t} \right)}^2} + {{\left( {0.8 - 0.08t} \right)}^2} + {{\left( {1 - 0.24t} \right)}^2}}$ M1A1

$\left( { = \sqrt {8.64 - 2.688t + 0.317{t^2}} } \right)$

[5 marks]

c.i.

minimum when $\frac{{{\text{d}}D}}{{{\text{d}}t}} = 0$ (M1)

t = 3.83 A1

[2 marks]

c.ii.

0.511 (km) A1

[1 mark]

c.iii.

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

c.iii.

The points A, B and C have the following position vectors with respect to an origin O.

$\overrightarrow {{\rm{OA}}} = 2$ i + j – 2k

$\overrightarrow {{\rm{OB}}} = 2$ i – j + 2k

$\overrightarrow {{\rm{OC}}} =$ i + 3j + 3k

The plane Π $_2$ contains the points O, A and B and the plane Π $_3$ contains the points O, A and C.

Find the vector equation of the line (BC).

[3]

Determine whether or not the lines (OA) and (BC) intersect.

[6]

Find the Cartesian equation of the plane Π $_1$ , which passes through C and is perpendicular to $\overrightarrow {{\rm{OA}}}$ .

[3]

Show that the line (BC) lies in the plane Π $_1$ .

[2]

Verify that 2j + k is perpendicular to the plane Π $_2$ .

[3]

Find a vector perpendicular to the plane Π $_3$ .

[1]

Find the acute angle between the planes Π $_2$ and Π $_3$ .

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\overrightarrow {{\rm{BC}}}$ = (i + 3j + 3k) $-$ (2i $-$ j + 2k) = $-$ i + 4j + k (A1)

r = (2i $-$ j + 2k) + $\lambda$ ( $-$ i + 4j + k)

(or r = (i + 3j + 3k) + $\lambda$ ( $-$ i + 4j + k) (M1)A1

Note: Do not award A1 unless r = or equivalent correct notation seen.

[3 marks]

attempt to write in parametric form using two different parameters AND equate M1

$2\mu = 2 - \lambda$

$\mu = - 1 + 4\lambda$

$- 2\mu = 2 + \lambda$ A1

attempt to solve first pair of simultaneous equations for two parameters M1

solving first two equations gives $\lambda = \frac{4}{9},{\text{ }}\mu = \frac{7}{9}$ (A1)

substitution of these two values in third equation (M1)

since the values do not fit, the lines do not intersect R1

Note: Candidates may note that adding the first and third equations immediately leads to a contradiction and hence they can immediately deduce that the lines do not intersect.

[6 marks]

METHOD 1

plane is of the form r $\bullet$ (2i + j $-$ 2k) = d (A1)

d = (i + 3j + 3k) $\bullet$ (2i + j $-$ 2k) = $-$ 1 (M1)

hence Cartesian form of plane is $2x + y - 2z = - 1$ A1

METHOD 2

plane is of the form $2x + y - 2z = d$ (A1)

substituting $(1,{\text{ }}3,{\text{ }}3)$ (to find gives $2 + 3 - 6 = - 1$ ) (M1)

hence Cartesian form of plane is $2x + y - 2z = - 1$ A1

[3 marks]

METHOD 1

attempt scalar product of direction vector BC with normal to plane M1

( $-$ i + 4j + k) $\bullet$ (2i + j $-$ 2k) $= - 2 + 4 - 2$

$= 0$ A1

hence BC lies in Π $_1$ AG

METHOD 2

substitute eqn of line into plane M1

${\text{line }}r = \left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ 2 \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} { - 1} \\ 4 \\ 1 \end{array}} \right).{\text{ Plane }}{\pi _1}:2x + y - 2z = - 1$

$2(2 - \lambda ) + ( - 1 + 4\lambda ) - 2(2 + \lambda )$

$= - 1$ A1

hence BC lies in Π $_1$ AG

Note: Candidates may also just substitute $2i - j + 2k$ into the plane since they are told C lies on ${\pi _1}$ .

Note: Do not award A1FT.

[2 marks]

METHOD 1

applying scalar product to $\overrightarrow {{\rm{OA}}}$ and $\overrightarrow {{\rm{OB}}}$ M1

(2j + k) $\bullet$ (2i + j $-$ 2k) = 0 A1

(2j + k) $\bullet$ (2i $-$ j + 2k) =0 A1

METHOD 2

attempt to find cross product of $\overrightarrow {{\rm{OA}}}$ and $\overrightarrow {{\rm{OB}}}$ M1

plane Π $_2$ has normal $\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OB}}}$ = $-$ 8j $-$ 4k A1

since $-$ 8j $-$ 4k = $-$ 4(2j + k), 2j + k is perpendicular to the plane Π $_2$ R1

[3 marks]

plane Π $_3$ has normal $\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OC}}}$ = 9i $-$ 8j + 5k A1

[1 mark]

attempt to use dot product of normal vectors (M1)

$\cos \theta = \frac{{(2j + k) \bullet (9i - 8j + 5k)}}{{\left| {2j + k} \right|\left| {9i - 8j + 5k} \right|}}$ (M1)

$= \frac{{ - 11}}{{\sqrt 5 \sqrt {170} }}\,\,\,( = - 0.377 \ldots )$ (A1)

Note: Accept $\frac{{11}}{{\sqrt 5 \sqrt {170} }}$ . acute angle between planes $= 67.8^\circ \,\,\,{\text{(}} = 1.18^\circ )$ A1

[4 marks]

Examiners report

[N/A]

Consider the planes $Π_{1}$ and $Π_{2}$ with the following equations.

$Π_{1} : 3 x + 2 y + z = 6$

$Π_{2} : x - 2 y + z = 4$

Find a Cartesian equation of the plane $Π_{3}$ which is perpendicular to $Π_{1}$ and $Π_{2}$ and passes through the origin $(0, 0, 0)$ .

[3]

Find the coordinates of the point where $Π_{1}$ , $Π_{2}$ and $Π_{3}$ intersect.

[2]

Markscheme

attempt to find a vector perpendicular to $Π_{1}$ and $Π_{2}$ using a cross product (M1)

$(\begin{matrix} 3 \\ 2 \\ 1 \end{matrix}) \times (\begin{matrix} 1 \\ - 2 \\ 1 \end{matrix}) = (2 - (- 2)) i + (1 - 3) j + (- 6 - 2) k$

$= (\begin{matrix} 4 \\ - 2 \\ - 8 \end{matrix}) (= 2 (\begin{matrix} 2 \\ - 1 \\ - 4 \end{matrix}))$ (A1)

equation is $4 x - 2 y - 8 z = 0 (\Rightarrow 2 x - y - 4 z = 0)$ A1

[3 marks]

attempt to solve $3$ simultaneous equations in $3$ variables (M1)

$(\frac{41}{21}, - \frac{10}{21}, \frac{23}{21}) (= (1.95, - 0.476, 1.10))$ A1

[2 marks]

Examiners report

[N/A]

Iqbal attempts three practice papers in mathematics. The probability that he passes the first paper is 0.6. Whenever he gains a pass in a paper, his confidence increases so that the probability of him passing the next paper increases by 0.1. Whenever he fails a paper the probability of him passing the next paper is 0.6.

Complete the given probability tree diagram for Iqbal’s three attempts, labelling each branch with the correct probability.

[3]

Calculate the probability that Iqbal passes at least two of the papers he attempts.

[2]

Find the probability that Iqbal passes his third paper, given that he passed only one previous paper.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

A1A1A1

Note: Award A1 for each correct column of probabilities.

[3 marks]

probability (at least twice) =

EITHER

$\left( {0.6 \times 0.7 \times 0.8} \right) + \left( {0.6 \times 0.7 \times 0.2} \right) + \left( {0.6 \times 0.3 \times 0.6} \right) + \left( {0.4 \times 0.6 \times 0.7} \right)$ (M1)

$\left( {0.6 \times 0.7} \right) + \left( {0.6 \times 0.3 \times 0.6} \right) + \left( {0.4 \times 0.6 \times 0.7} \right)$ (M1)

Note: Award M1 for summing all required probabilities.

THEN

= 0.696 A1

[2 marks]

P(passes third paper given only one paper passed before)

$= \frac{{{\text{P}}\,\left( {{\text{passes third AND only one paper passed before}}} \right)}}{{{\text{P}}\,\left( {{\text{passes once in first two papers}}} \right)}}$ (M1)

$= \frac{{\left( {0.6 \times 0.3 \times 0.6} \right) + \left( {0.4 \times 0.6 \times 0.7} \right)}}{{\left( {0.6 \times 0.3} \right) + \left( {0.4 \times 0.6} \right)}}$ A1

= 0.657 A1

[3 marks]

Examiners report

[N/A]

The diagram shows two circles with centres at the points A and B and radii $2r$ and $r$ , respectively. The point B lies on the circle with centre A. The circles intersect at the points C and D.

N16/5/MATHL/HP2/ENG/TZ0/09

Let $\alpha$ be the measure of the angle CAD and $\theta$ be the measure of the angle CBD in radians.

Find an expression for the shaded area in terms of $\alpha$ , $\theta$ and $r$ .

[3]

Show that $\alpha = 4\arcsin \frac{1}{4}$ .

[2]

Hence find the value of $r$ given that the shaded area is equal to 4.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$A = 2(\alpha - \sin \alpha ){r^2} + \frac{1}{2}(\theta - \sin \theta ){r^2}$ M1A1A1

Note: Award M1A1A1 for alternative correct expressions eg. $A = 4\left( {\frac{\alpha }{2} - \sin \frac{\alpha }{2}} \right){r^2} + \frac{1}{2}\theta {r^2}$ .

[3 marks]

METHOD 1

consider for example triangle ADM where M is the midpoint of BD M1

$\sin \frac{\alpha }{4} = \frac{1}{4}$ A1

$\frac{\alpha }{4} = \arcsin \frac{1}{4}$

$\alpha = 4\arcsin \frac{1}{4}$ AG

METHOD 2

attempting to use the cosine rule (to obtain $1 - \cos \frac{\alpha }{2} = \frac{1}{8}$ ) M1

$\sin \frac{\alpha }{4} = \frac{1}{4}$ (obtained from $\sin \frac{\alpha }{4} = \sqrt {\frac{{1 - \cos \frac{\alpha }{2}}}{2}}$ ) A1

$\frac{\alpha }{4} = \arcsin \frac{1}{4}$

$\alpha = 4\arcsin \frac{1}{4}$ AG

METHOD 3

$\sin \left( {\frac{\pi }{2} - \frac{\alpha }{4}} \right) = 2\sin \frac{\alpha }{2}$ where $\frac{\theta }{2} = \frac{\pi }{2} - \frac{\alpha }{4}$

$\cos \frac{\alpha }{4} = 4\sin \frac{\alpha }{4}\cos \frac{\alpha }{4}$ M1

Note: Award M1 either for use of the double angle formula or the conversion from sine to cosine.

$\frac{1}{4} = \sin \frac{\alpha }{4}$ A1

$\frac{\alpha }{4} = \arcsin \frac{1}{4}$

$\alpha = 4\arcsin \frac{1}{4}$ AG

[2 marks]

(from triangle ADM), $\theta = \pi - \frac{\alpha }{2}{\text{ }}\left( { = \pi - 2\arcsin \frac{1}{4} = 2\arcsin \frac{1}{4} = 2.6362 \ldots } \right)$ A1

attempting to solve $2(\alpha - \sin \alpha ){r^2} + \frac{1}{2}(\theta - \sin \theta ){r^2} = 4$

with $\alpha = 4\arcsin \frac{1}{4}$ and $\theta = \pi - \frac{\alpha }{2}{\text{ }}\left( { = 2\arccos \frac{1}{4}} \right)$ for $r$ (M1)

$r = 1.69$ A1

[3 marks]

Examiners report

[N/A]

The plane П₁ contains the points P(1, 6, −7) , Q(0, 1, 1) and R(2, 0, −4).

The Cartesian equation of the plane П₂ is given by $x - 3y - z = 3$ .

The Cartesian equation of the plane П₃ is given by $ax + by + cz = 1$ .

Consider the case that П₃ contains $L$ .

Find the Cartesian equation of the plane containing P, Q and R.

[6]

Given that П₁ and П₂ meet in a line $L$ , verify that the vector equation of $L$ can be given by r $= \left( {\begin{array}{*{20}{c}} {\frac{5}{4}} \\ 0 \\ { - \frac{7}{4}} \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} {\frac{1}{2}} \\ 1 \\ { - \frac{5}{2}} \end{array}} \right)$ .

[3]

Given that П₃ is parallel to the line $L$ , show that $a + 2b - 5c = 0$ .

[1]

Show that $5a - 7c = 4$ .

[2]

d.i.

Given that П₃ is equally inclined to both П₁ and П₂, determine two distinct possible Cartesian equations for П₃.

[7]

d.ii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

for example

$\overrightarrow {{\text{PQ}}} = \left( {\begin{array}{*{20}{c}} { - 1} \\ { - 5} \\ 8 \end{array}} \right)$ , $\overrightarrow {{\text{PR}}} = \left( {\begin{array}{*{20}{c}} 1 \\ { - 6} \\ 3 \end{array}} \right)$ A1A1

$\overrightarrow {{\text{PQ}}} \times \overrightarrow {{\text{PR}}}$ = 33i + 11j + 11k (M1)A1

r.n = a.n

$33x + 11y + 11z = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {33} \\ {11} \\ {11} \end{array}} \right) = 22$ (M1)

$\Rightarrow 3x + y + z = 2$ or equivalent A1

METHOD 2

assume plane can be written as $ax + by + cz = 1$ M1

substituting each set of coordinates gives the system of equations:

$a + 6b - 7c = 1$

$0a + b + c = 1$

$2a + 0b - 4c = 1$ A1

solving by GDC (M1)

$a = \frac{3}{2}$ , $b = \frac{1}{2}$ , $C = \frac{1}{2}$ A1A1A1

$\Rightarrow \frac{3}{2}x + \frac{1}{2}y + \frac{1}{2}z = 1$ or equivalent

[6 marks]

METHOD 1

substitution of equation of line into both equations of planes M1

$3\left( {\frac{5}{4} + \frac{\lambda }{2}} \right) + \left( { - \frac{7}{4} - \frac{{5\lambda }}{2}} \right) = 2$ A1

$\left( {\frac{5}{4} + \frac{\lambda }{2}} \right) - 3\lambda - \left( { - \frac{7}{4} - \frac{{5\lambda }}{2}} \right) = 3$ A1

METHOD 2

adding Π₁ and Π₂ gives $4x - 2y = 5$ M1

given $y = \lambda \Rightarrow x = \frac{5}{4} + \frac{\lambda }{2}$ A1

$z = 2 - y - 3x = - \frac{7}{4} - \frac{{5\lambda }}{2}$ A1

⇒r $= \left( {\begin{array}{*{20}{c}} {\frac{5}{4}} \\ 0 \\ { - \frac{7}{4}} \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} {\frac{1}{2}} \\ 1 \\ { - \frac{5}{2}} \end{array}} \right)$ AG

METHOD 3

n₁ × n₂ = $\left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { - 10} \end{array}} \right)$ A1

$= 4\left( {\begin{array}{*{20}{c}} {\frac{1}{2}} \\ 1 \\ { - \frac{5}{2}} \end{array}} \right)$ R1

common point $\frac{5}{4} - 3\left( 0 \right) - \left( { - \frac{7}{4}} \right) = 3$ and $- 3\left( {\frac{5}{4}} \right) - 0 - \left( { - \frac{7}{4}} \right) = - 2$ A1

[3 marks]

normal to П₃ is perpendicular to direction of $L$

$\Rightarrow \left( {\begin{array}{*{20}{c}} a \\ b \\ c \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ { - 5} \end{array}} \right) = 0$ A1

⇒ $a + 2b - 5c = 0$ AG

[1 mark]

substituting $\left( {\begin{array}{*{20}{c}} {\frac{5}{4}} \\ 0 \\ { - \frac{7}{4}} \end{array}} \right)$ into П₃: M1

$\frac{{5a}}{4} - \frac{{7c}}{4} = 1$ A1

$5a - 7c = 4$ AG

[2 marks]

d.i.

attempt to find scalar products for П₁ and П₃, П₂ and П₃.

and equating M1

$\frac{{3a + b + C}}{{\sqrt {11} \sqrt {{a^2} + {b^2} + {c^2}} }} = \frac{{a - 3b - c}}{{\sqrt {11} \sqrt {{a^2} + {b^2} + {c^2}} }}$ M1

Note: Accept $3a + b + c = a - 3b - c$ .

$\Rightarrow a + 2b + c = 0$ A1

attempt to solve $a + 2b + c = 0$ , $a + 2b - 5c = 0$ , $5a - 7c = 4$ M1

$\Rightarrow a = \frac{4}{5}{\text{,}}\,\,b = - \frac{2}{5}{\text{,}}\,\,c = 0$ A1

hence equation is $\frac{{4x}}{5} - \frac{{2y}}{5} = 1$

for second equation:

$\frac{{3a + b + C}}{{\sqrt {11} \sqrt {{a^2} + {b^2} + {c^2}} }} = - \frac{{a - 3b - c}}{{\sqrt {11} \sqrt {{a^2} + {b^2} + {c^2}} }}$ (M1)

$\Rightarrow 2a - b = 0$

attempt to solve $2a - b = 0$ , $a + 2b - 5c = 0$ , $5a - 7c = 4$ M1

⇒ $a = - 2$ , $b = - 4$ , $c = - 2$ A1

hence equation is $- 2x - 4y - 2z = 1$

[7 marks]

d.ii.

Examiners report

[N/A]

d.i.

[N/A]

d.ii.

A scientist conducted a nine-week experiment on two plants, $A$ and $B$ , of the same species. He wanted to determine the effect of using a new plant fertilizer. Plant $A$ was given fertilizer regularly, while Plant $B$ was not.

The scientist found that the height of Plant $A, h_{A} cm$ , at time $t$ weeks can be modelled by the function $h_{A} (t) = \sin (2 t + 6) + 9 t + 27$ , where $0 \leq t \leq 9$ .

The scientist found that the height of Plant $B, h_{B} cm$ , at time $t$ weeks can be modelled by the function $h_{B} (t) = 8 t + 32$ , where $0 \leq t \leq 9$ .

Use the scientist’s models to find the initial height of

Plant $B$ .

[1]

a.i.

Plant $A$ correct to three significant figures.

[2]

a.ii.

Find the values of $t$ when $h_{A} (t) = h_{B} (t)$ .

[3]

For $t > 6$ , prove that Plant $A$ was always taller than Plant $B$ .

[3]

For $0 \leq t \leq 9$ , find the total amount of time when the rate of growth of Plant $B$ was greater than the rate of growth of Plant $A$ .

[6]

Markscheme

$32$ (cm) A1

[1 mark]

a.i.

$h_{A} (0) = \sin (6) + 27$ (M1)

$= 26.7205 \dots$

$= 26.7$ (cm) A1

[2 marks]

a.ii.

attempts to solve $h_{A} (t) = h_{B} (t)$ for $t$ (M1)

$t = 4.0074 \dots, 4.7034 \dots, 5.88332 \dots$

$t = 4.01, 4.70, 5.88$ (weeks) A2

[3 marks]

$h_{A} (t) - h_{B} (t) = \sin (2 t + 6) + t - 5$ A1

EITHER

for $t > 6, t - 5 > 1$ A1

and as $\sin (2 t + 6) \geq - 1 \Rightarrow h_{A} (t) - h_{B} (t) > 0$ R1

the minimum value of $\sin (2 t + 6) = - 1$ R1

so for $t > 6, h_{A} (t) - h_{B} (t) = t - 6 > 0$ A1

THEN

hence for $t > 6$ , Plant $A$ was always taller than Plant $B$ AG

[3 marks]

recognises that $h_{A}' (t)$ and $h_{B}' (t)$ are required (M1)

attempts to solve $h_{A}' (t) = h_{B}' (t)$ for $t$ (M1)

$t = 1.18879 \dots$ and $2.23598 \dots$ OR $4.33038 \dots$ and $5.37758 \dots$ OR $7.47197 \dots$ and $8.51917 \dots$ (A1)

Note: Award full marks for $t = \frac{4 π}{3} - 3, \frac{5 π}{3} - 3, (\frac{7 π}{3} - 3, \frac{8 π}{3} - 3 \frac{10 π}{3} - 3, \frac{11 π}{3} - 3)$ .

Award subsequent marks for correct use of these exact values.

$1.18879 \dots < t < 2.23598 \dots$ OR $4.33038 \dots < t < 5.37758 \dots$ OR $7.47197 \dots < t < 8.51917 \dots$ (A1)

attempts to calculate the total amount of time (M1)

$3 (2.2359 \dots - 1.1887 \dots) (= 3 ((\frac{5 π}{3} - 3) - (\frac{4 π}{3} - 3)))$

$= 3.14 (= π)$ (weeks) A1

[6 marks]

Examiners report

Part (a) In general, very well done, most students scored full marks. Some though had an incorrect answer for part(a)(ii) because they had their GDC in degrees.

Part (b) Well attempted. Some accuracy errors and not all candidates listed all three values.

Part (c) Most students tried a graphical approach (but this would only get them one out of three marks) and only some provided a convincing algebraic justification. Many candidates tried to explain in words without a convincing mathematical justification or used numerical calculations with specific time values. Some arrived at the correct simplified equation for the difference in heights but could not do much with it. Then only a few provided a correct mathematical proof.

Part (d) In general, well attempted by many candidates. The common error was giving the answer as 3.15 due to the pre-mature rounding. Some candidates only provided the values of time when the rates are equal, some intervals rather than the total time.

a.i.

[N/A]

a.ii.

[N/A]

Consider the following diagram.

The sides of the equilateral triangle ABC have lengths 1 m. The midpoint of [AB] is denoted by P. The circular arc AB has centre, M, the midpoint of [CP].

Find AM.

[3]

a.i.

Find ${\text{A}}\mathop {\text{M}}\limits^ \wedge {\text{P}}$ in radians.

[2]

a.ii.

Find the area of the shaded region.

[3]

Markscheme

METHOD 1

PC $= \frac{{\sqrt 3 }}{2}$ or 0.8660 (M1)

PM $= \frac{1}{2}$ PC $= \frac{{\sqrt 3 }}{4}$ or 0.4330 (A1)

AM $= \sqrt {\frac{1}{4} + \frac{3}{{16}}}$

$= \frac{{\sqrt 7 }}{4}$ or 0.661 (m) A1

METHOD 2

using the cosine rule

AM² $= {1^2} + {\left( {\frac{{\sqrt 3 }}{4}} \right)^2} - 2 \times \frac{{\sqrt 3 }}{4} \times {\text{cos}}\left( {30^\circ } \right)$ M1A1

AM $= \frac{{\sqrt 7 }}{4}$ or 0.661 (m) A1

[3 marks]

a.i.

tan ( ${\text{A}}\mathop {\text{M}}\limits^ \wedge {\text{P}}$ ) $= \frac{2}{{\sqrt 3 }}$ or equivalent (M1)

= 0.857 A1

[2 marks]

a.ii.

EITHER

$\frac{1}{2}{\text{A}}{{\text{M}}^2}\left( {2\,{\text{A}}\mathop {\text{M}}\limits^ \wedge {\text{P}} - {\text{sin}}\left( {2\,{\text{A}}\mathop {\text{M}}\limits^ \wedge {\text{P}}} \right)} \right)$ (M1)A1

$\frac{1}{2}{\text{A}}{{\text{M}}^2} \times 2\,{\text{A}}\mathop {\text{M}}\limits^ \wedge {\text{P}} - = \frac{{\sqrt 3 }}{8}$ (M1)A1

= 0.158(m²) A1

Note: Award M1 for attempting to calculate area of a sector minus area of a triangle.

[3 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

Let $f\left( x \right) = {\text{tan}}\left( {x + \pi } \right){\text{cos}}\left( {x - \frac{\pi }{2}} \right)$ where $0 < x < \frac{\pi }{2}$ .

Express $f\left( x \right)$ in terms of sin $x$ and cos $x$ .

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

${\text{tan}}\left( {x + \pi } \right) = \tan x\left( { = \frac{{{\text{sin}}\,x}}{{{\text{cos}}\,x}}} \right)$ (M1)A1

${\text{cos}}\left( {x - \frac{\pi }{2}} \right) = {\text{sin}}\,x$ (M1)A1

Note: The two M1s can be awarded for observation or for expanding.

${\text{tan}}\left( {x + \pi } \right) = {\text{cos}}\left( {x - \frac{\pi }{2}} \right) = \frac{{{\text{si}}{{\text{n}}^2}\,x}}{{{\text{cos}}\,x}}$ A1

[5 marks]

Examiners report

[N/A]

Consider the vectors $a$ and $b$ such that $a = (\begin{matrix} 12 \\ - 5 \end{matrix})$ and $|b| = 15$ .

Consider the vector $p$ such that $p = a + b$ .

Consider the vector $q$ such that $q = (\begin{matrix} x \\ y \end{matrix})$ , where $x, y \in ℝ^{+}$ .

Find the possible range of values for $|a + b|$ .

[2]

Given that $|a + b|$ is a minimum, find $p$ .

[2]

Find $q$ such that $| q | = | b |$ and $q$ is perpendicular to $a$ .

[5]

Markscheme

$|a| = \sqrt{12^{2} + {(- 5)}^{2}} (= 13)$ (A1)

$2 \leq |a + b| \leq 28$ (accept min $2$ and max $28$ ) A1

Note: Award (A1)A0 for $2$ and $28$ seen with no indication that they are the endpoints of an interval.

[2 marks]

recognition that $p$ or $b$ is a negative multiple of $a$ (M1)

$p = - 2 \hat{a}$ OR $b = - \frac{15}{13} a (= - \frac{15}{13} (\begin{matrix} 12 \\ - 5 \end{matrix}))$

$p = - \frac{2}{13} (\begin{matrix} 12 \\ - 5 \end{matrix}) (= (\begin{matrix} - 1.85 \\ 0.769 \end{matrix}))$ A1

[2 marks]

METHOD 1

$q$ is perpendicular to $(\begin{matrix} 12 \\ - 5 \end{matrix})$

$\Rightarrow q$ is in the direction $(\begin{matrix} 5 \\ 12 \end{matrix})$ (M1)

$q = k (\begin{matrix} 5 \\ 12 \end{matrix})$ (A1)

$(|q| =) \sqrt{{(5 k)}^{2} + {(12 k)}^{2}} = 15$ (M1)

$k = \frac{15}{13}$ (A1)

$q = \frac{15}{13} (\begin{matrix} 5 \\ 12 \end{matrix}) (= (\begin{matrix} \frac{75}{13} \\ \frac{180}{13} \end{matrix}) = (\begin{matrix} 5.77 \\ 13.8 \end{matrix}))$ A1

METHOD 2

$q$ is perpendicular to $(\begin{matrix} 12 \\ - 5 \end{matrix})$

attempt to set scalar product $q . a = 0$ OR product of gradients $= - 1$ (M1)

$12 x - 5 y = 0$ (A1)

$(|q| =) \sqrt{x^{2} + y^{2}} = 15$

attempt to solve simultaneously to find a quadratic in $x$ or $y$ (M1)

$x^{2} + {(\frac{12 x}{5})}^{2} = 15^{2}$ OR ${(\frac{5 y}{12})}^{2} + y^{2} = 15^{2}$

$q = (\begin{matrix} \frac{75}{13} \\ \frac{180}{13} \end{matrix}) (= (\begin{matrix} 5.77 \\ 13.8 \end{matrix}))$ A1A1

Note: Award A1 independently for each value. Accept values given as $x = \frac{75}{13}$ and $y = \frac{180}{13}$ or equivalent.

[5 marks]

Examiners report

[N/A]

Three points $A (3, 0, 0), B (0, - 2, 0)$ and $C (1, 1, - 7)$ lie on the plane $Π_{1}$ .

Plane $Π_{2}$ has equation $3 x - y + 2 z = 2$ .

The plane $Π_{3}$ is given by $2 x - 2 z = 3$ . The line $L$ and the plane $Π_{3}$ intersect at the point $P$ .

The point $B (0, - 2, 0)$ lies on $L$ .

Find the vector $\vec{AB}$ and the vector $\vec{AC}$ .

[2]

a.i.

Hence find the equation of $Π_{1}$ , expressing your answer in the form $a x + b y + c z = d$ , where $a, b, c, d \in ℤ$ .

[5]

a.ii.

The line $L$ is the intersection of $Π_{1}$ and $Π_{2}$ . Verify that the vector equation of $L$ can be written as $r = (\begin{matrix} 0 \\ - 2 \\ 0 \end{matrix}) + λ (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix})$ .

[2]

Show that at the point $P, λ = \frac{3}{4}$ .

[2]

c.i.

Hence find the coordinates of $P$ .

[1]

c.ii.

Find the reflection of the point $B$ in the plane $Π_{3}$ .

[7]

d.i.

Hence find the vector equation of the line formed when $L$ is reflected in the plane $Π_{3}$ .

[2]

d.ii.

Markscheme

attempts to find either $\vec{AB}$ or $\vec{AC}$ (M1)

$\vec{AB} = (\begin{matrix} - 3 \\ - 2 \\ 0 \end{matrix})$ and $\vec{AC} = (\begin{matrix} - 2 \\ 1 \\ - 7 \end{matrix})$ A1

[2 marks]

a.i.

METHOD 1

attempts to find $\vec{AB} \times \vec{AC}$ (M1)

$\vec{AB} \times \vec{AC} = (\begin{matrix} 14 \\ - 21 \\ - 7 \end{matrix})$ A1

EITHER

equation of plane is of the form $14 x - 21 y - 7 z = d (2 x - 3 y - z = d)$ (A1)

substitutes a valid point e.g $(3, 0, 0)$ to obtain a value of $d$ M1

$d = 42 (d = 6)$

attempts to use $r \cdot n = a \cdot n$ (M1)

$r \cdot (\begin{matrix} 14 \\ - 21 \\ - 7 \end{matrix}) = (\begin{matrix} 3 \\ 0 \\ 0 \end{matrix}) \cdot (\begin{matrix} 14 \\ - 21 \\ - 7 \end{matrix}) (r \cdot (\begin{matrix} 14 \\ - 21 \\ - 7 \end{matrix}) = 42)$ A1

$r \cdot (\begin{matrix} 2 \\ - 3 \\ - 1 \end{matrix}) = (\begin{matrix} 3 \\ 0 \\ 0 \end{matrix}) \cdot (\begin{matrix} 2 \\ - 3 \\ - 1 \end{matrix}) (r \cdot (\begin{matrix} 2 \\ - 3 \\ - 1 \end{matrix}) = 6)$

THEN

$14 x - 21 y - 7 z = 42 (2 x - 3 y - z = 6)$ A1

METHOD 2

equation of plane is of the form $(\begin{matrix} x \\ y \\ z \end{matrix}) = (\begin{matrix} 3 \\ 0 \\ 0 \end{matrix}) + s (\begin{matrix} - 3 \\ - 2 \\ 0 \end{matrix}) + t (\begin{matrix} - 2 \\ 1 \\ - 7 \end{matrix})$ A1

attempts to form equations for $x, y, z$ in terms of their parameters (M1)

$x = 3 - 3 s - 2 t, y = - 2 s + t, z = - 7 t$ A1

eliminates at least one of their parameters (M1)

for example, $2 x - 3 y = 6 - 7 t (\Rightarrow 2 x - 3 y = 6 + z)$

$2 x - 3 y - z = 6$ A1

[5 marks]

a.ii.

METHOD 1

substitutes $r = (\begin{matrix} 0 \\ - 2 \\ 0 \end{matrix}) + λ (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix})$ into their $Π_{1}$ and $Π_{2}$ (given) (M1)

$Π_{1} : 2 λ - 3 (- 2 + λ) - (- λ) = 6$ and $Π_{2} : 3 λ - 3 (- 2 + λ) + 2 (- λ) = 2$ A1

Note: Award (M1)A0 for correct verification using a specific value of $λ$ .

so the vector equation of $L$ can be written as $r = (\begin{matrix} 0 \\ - 2 \\ 0 \end{matrix}) + λ (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix})$ AG

METHOD 2

EITHER

attempts to find $(\begin{matrix} 2 \\ - 3 \\ - 1 \end{matrix}) \times (\begin{matrix} 3 \\ - 1 \\ 2 \end{matrix})$ M1

$= (\begin{matrix} - 7 \\ - 7 \\ 7 \end{matrix})$

$(\begin{matrix} 2 \\ - 3 \\ - 1 \end{matrix}) \cdot (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix}) = (2 - 3 + 1) = 0$ and $(\begin{matrix} 3 \\ - 1 \\ 2 \end{matrix}) \cdot (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix}) = (3 - 1 - 2) = 0$ M1

THEN

substitutes $(0, - 2, 0)$ into $Π_{1}$ and $Π_{2}$

$Π_{1} : 2 (0) - 3 (- 2) - (0) = 6$ and $Π_{2} : 3 (0) - (- 2) + 2 (0) = 2$ A1

so the vector equation of $L$ can be written as $r = (\begin{matrix} 0 \\ - 2 \\ 0 \end{matrix}) + λ (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix})$ AG

METHOD 3

attempts to solve $2 x - 3 y - z = 6$ and $3 x - y + 2 z = 2$ (M1)

for example, $x = - λ, y = - 2 - λ, z = λ$ A1

Note: Award A1 for substituting $x = 0$ (or $y = - 2$ or $z = 0$ ) into $Π_{1}$ and $Π_{2}$ and solving simultaneously. For example, solving $- 3 y - z = 6$ and $- y + 2 z = 2$ to obtain $y = - 2$ and $z = 0$ .

so the vector equation of $L$ can be written as $r = (\begin{matrix} 0 \\ - 2 \\ 0 \end{matrix}) + λ (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix})$ AG

[2 marks]

substitutes the equation of $L$ into the equation of $Π_{3}$ (M1)

$2 λ + 2 λ = 3 \Rightarrow 4 λ = 3$ A1

$λ = \frac{3}{4}$ AG

[2 marks]

c.i.

$P$ has coordinates $(\frac{3}{4}, - \frac{5}{4}, - \frac{3}{4})$ A1

[1 mark]

c.ii.

normal to $Π_{3}$ is $n = (\begin{matrix} 2 \\ 0 \\ - 2 \end{matrix})$ (A1)

Note: May be seen or used anywhere.

considers the line normal to $Π_{3}$ passing through $B (0, - 2, 0)$ (M1)
$r = (\begin{matrix} 0 \\ - 2 \\ 0 \end{matrix}) + μ (\begin{matrix} 2 \\ 0 \\ - 2 \end{matrix})$ A1

EITHER

finding the point on the normal line that intersects $Π_{3}$
attempts to solve simultaneously with plane $2 x - 2 z = 3$ (M1)

$4 μ + 4 μ = 3$

$μ = \frac{3}{8}$ A1

point is $(\frac{3}{4}, - 2, - \frac{3}{4})$

$((\begin{matrix} 2 μ \\ - 2 \\ - 2 μ \end{matrix}) - (\begin{matrix} \frac{3}{4} \\ - \frac{5}{4} \\ - \frac{3}{4} \end{matrix})) \cdot (\begin{matrix} 2 \\ 0 \\ - 2 \end{matrix}) = 0$ (M1)

$4 μ - \frac{3}{2} + 4 μ - \frac{3}{2} = 0$

$μ = \frac{3}{8}$ A1

attempts to find the equation of the plane parallel to $Π_{3}$ containing $B' (x - z = 3)$ and solve simultaneously with $L$ (M1)

$2 μ' + 2 μ' = 3$

$μ' = \frac{3}{4}$ A1

THEN

so, another point on the reflected line is given by

$r = (\begin{matrix} 0 \\ - 2 \\ 0 \end{matrix}) + \frac{3}{4} (\begin{matrix} 2 \\ 0 \\ - 2 \end{matrix})$ (A1)

$\Rightarrow B' (\frac{3}{2}, - 2, - \frac{3}{2})$ A1

[7 marks]

d.i.

EITHER

attempts to find the direction vector of the reflected line using their $P$ and $B'$ (M1)

$\vec{PB'} = (\begin{matrix} \frac{3}{4} \\ - \frac{3}{4} \\ - \frac{3}{4} \end{matrix})$

attempts to find their direction vector of the reflected line using a vector approach (M1)

$\vec{PB'} = \vec{PB} + \vec{BB'} = - \frac{3}{4} (\begin{matrix} 1 \\ 1 \\ - 1 \end{matrix}) + \frac{3}{2} (\begin{matrix} 1 \\ 0 \\ - 1 \end{matrix})$

THEN

$r = (\begin{matrix} \frac{3}{2} \\ - 2 \\ - \frac{3}{2} \end{matrix}) + λ (\begin{matrix} \frac{3}{4} \\ - \frac{3}{4} \\ - \frac{3}{4} \end{matrix})$ (or equivalent) A1

Note: Award A0 for either ' $r =$ ' or ' $(\begin{matrix} x \\ y \\ z \end{matrix}) =$ ' not stated. Award A0 for ' $L' =$ '

[2 marks]

d.ii.

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

d.i.

[N/A]

d.ii.

The points $A (5, - 2, 5)$ , $B (5, 4, - 1)$ , $C (- 1, - 2, - 1)$ and $D (7, - 4, - 3)$ are the vertices of a right-pyramid.

The line $L$ passes through the point $D$ and is perpendicular to $Π$ .

Find the vectors $\vec{AB}$ and $\vec{AC}$ .

[2]

Use a vector method to show that $B \hat{A} C = 60 °$ .

[3]

Show that the Cartesian equation of the plane $Π$ that contains the triangle $ABC$ is $- x + y + z = - 2$ .

[3]

Find a vector equation of the line $L$ .

[1]

d.i.

Hence determine the minimum distance, $d_{min}$ , from $D$ to $Π$ .

[4]

d.ii.

Find the volume of right-pyramid $ABCD$ .

[4]

Markscheme

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

$\vec{AB} = (\begin{matrix} 0 \\ 6 \\ - 6 \end{matrix}) (= 6 (\begin{matrix} 0 \\ 1 \\ - 1 \end{matrix}))$ A1

$\vec{AC} = (\begin{matrix} - 6 \\ 0 \\ - 6 \end{matrix}) (= 6 (\begin{matrix} - 1 \\ 0 \\ - 1 \end{matrix}))$ A1

[2 marks]

attempts to use $\cos B \hat{A} C = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| |\vec{AC}|}$ (M1)

$= \frac{(\begin{matrix} 0 \\ 6 \\ - 6 \end{matrix}) \cdot (\begin{matrix} - 6 \\ 0 \\ - 6 \end{matrix})}{\sqrt{72} \times \sqrt{72}}$ A1

$= \frac{1}{2}$ A1

so $B \hat{A} C = 60 °$ AG

[3 marks]

attempts to find a vector normal to $Π$ M1

for example, $\vec{AB} \times \vec{AC} = (\begin{matrix} - 36 \\ 36 \\ 36 \end{matrix}) (= 36 (\begin{matrix} - 1 \\ 1 \\ 1 \end{matrix}))$ leading to A1

a vector normal to $Π$ is $n = (\begin{matrix} - 1 \\ 1 \\ 1 \end{matrix})$

EITHER

substitutes $(5, - 2, - 5)$ (or $(5, 4, - 1)$ or $(- 1, - 2, - 1)$ ) into $- x + y + z = d$ and attempts to find the value of $d$

for example, $d = - 5 - 2 + 5 (= - 2)$ M1

attempts to use $r \cdot n = a \cdot n$ M1

for example, $(\begin{matrix} x \\ y \\ z \end{matrix}) \cdot (\begin{matrix} - 1 \\ 1 \\ 1 \end{matrix}) = (\begin{matrix} 5 \\ - 2 \\ 5 \end{matrix}) \cdot (\begin{matrix} - 1 \\ 1 \\ 1 \end{matrix})$

THEN

leading to the Cartesian equation of $Π$ as $- x + y + z = - 2$ AG

[3 marks]

$r = (\begin{matrix} 7 \\ - 4 \\ - 3 \end{matrix}) + λ (\begin{matrix} - 1 \\ 1 \\ 1 \end{matrix}) (λ \in ℝ)$ A1

[1 mark]

d.i.

substitutes $x = 7 - λ, y = - 4 + λ, z = - 3 + λ$ into $- x + y + z = - 2$ (M1)

$- (7 - λ) + (- 4 + λ) + (- 3 + λ) = - 2 (3 λ = 12)$

$λ = 4$ A1

shows a correct calculation for finding $d_{min}$ , for example, attempts to find

$|4 (\begin{matrix} - 1 \\ 1 \\ 1 \end{matrix})|$ M1

$d_{min} = 4 \sqrt{3} (= 6.93)$ A1

[4 marks]

d.ii.

let the area of triangle $ABC$ be $A$

EITHER

attempts to find $A = \frac{1}{2} |\vec{AB} \times \vec{AC}|$ , for example M1

$A = \frac{1}{2} |(\begin{matrix} - 36 \\ 36 \\ 36 \end{matrix})|$

attempts to find $\frac{1}{2} |\vec{AB}| |\vec{AC}| \sin θ$ , for example M1

$A = \frac{1}{2} \times 6 \sqrt{2} \times 6 \sqrt{2} \times \frac{\sqrt{3}}{2}$ (where $\sin \frac{π}{3} = \frac{\sqrt{3}}{2}$ )

THEN

$A = 18 \sqrt{3} (= 31.2)$ A1

uses $V = \frac{1}{3} A h$ where $A$ is the area of triangle $ABC$ and $h = d_{min}$ M1

$V = \frac{1}{3} \times 18 \sqrt{3} \times 4 \sqrt{3}$

$= 72$ A1

[4 marks]

Examiners report

[N/A]

d.i.

[N/A]

d.ii.

[N/A]

In triangle ABC, AB = 5, BC = 14 and AC = 11.

Find all the interior angles of the triangle. Give your answers in degrees to one decimal place.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to apply cosine rule M1

${\text{cos}}\,{\text{A}} = \frac{{{5^2} + {{11}^2} - {{14}^2}}}{{2 \times 5 \times 11}} = - 0.4545 \ldots$

$\Rightarrow {\text{A}} = 117.03569 \ldots ^\circ$

$\Rightarrow {\text{A}} = 117.0^\circ$ A1

attempt to apply sine rule or cosine rule: M1

$\frac{{{\text{sin}}\,117.03569 \ldots ^\circ }}{{14}} = \frac{{{\text{sin}}\,{\text{B}}}}{{11}}$

$\Rightarrow {\text{B}} = 44.4153 \ldots ^\circ$

$\Rightarrow {\text{B}} = 44.4^\circ$ A1

${\text{C}} = 180^\circ - {\text{A}} - {\text{B}}$

${\text{C}} = 18.5^\circ$ A1

Note: Candidates may attempt to find angles in any order of their choosing.

[5 marks]

Examiners report

[N/A]

The following shape consists of three arcs of a circle, each with centre at the opposite vertex of an equilateral triangle as shown in the diagram.

For this shape, calculate

the perimeter.

[2]

the area.

[5]

Markscheme

each arc has length $r\theta = 6 \times \frac{\pi }{3} = 2\pi \,\left( { = 6.283 \ldots } \right)$ (M1)

perimeter is therefore $6\pi \,\left( { = 18.8} \right)$ (cm) A1

[2 marks]

area of sector, $s$ , is $\frac{1}{2}{r^2}\theta = 18 \times \frac{\pi }{3} = 6\pi \,\left( { = 18.84 \ldots } \right)$ (A1)

area of triangle, $t$ , is $\frac{1}{2} \times 6 \times 3\sqrt 3 = 9\sqrt 3 \,\left( { = 15.58 \ldots } \right)$ (M1)(A1)

Note: area of segment, $k$ , is 3.261… implies area of triangle

finding $3s - 2t$ or $3k + t$ or similar

area $= 3s - 2t = 18\pi - 18\sqrt 3 \,\left( { = 25.4} \right)$ (cm²) (M1)A1

[5 marks]

Examiners report

[N/A]

Barry is at the top of a cliff, standing 80 m above sea level, and observes two yachts in the sea.
“Seaview” $(S)$ is at an angle of depression of 25°.
“Nauti Buoy” $(N)$ is at an angle of depression of 35°.
The following three dimensional diagram shows Barry and the two yachts at S and N.
X lies at the foot of the cliff and angle ${\text{SXN}} =$ 70°.

N17/5/MATHL/HP2/ENG/TZ0/05

Find, to 3 significant figures, the distance between the two yachts.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to use tan, or sine rule, in triangle BXN or BXS (M1)

${\text{NX}} = 80\tan 55{\rm{^\circ }}\left( { = \frac{{80}}{{\tan 35{\rm{^\circ }}}} = 114.25} \right)$ (A1)

${\text{SX}} = 80\tan 65{\rm{^\circ }}\left( { = \frac{{80}}{{\tan 25{\rm{^\circ }}}} = 171.56} \right)$ (A1)

Attempt to use cosine rule M1

${\text{S}}{{\text{N}}^2} = {171.56^2} + {114.25^2} - 2 \times 171.56 \times 114.25\cos 70$ ° (A1)

${\text{SN}} = 171{\text{ }}({\text{m}})$ A1

Note: Award final A1 only if the correct answer has been given to 3 significant figures.

[6 marks]

Examiners report

[N/A]

Consider $\lim_{x \to 0} \frac{arctan (\cos x) - k}{x^{2}}$ , where $k \in ℝ$ .

Show that a finite limit only exists for $k = \frac{π}{4}$ .

[2]

Using l’Hôpital’s rule, show algebraically that the value of the limit is $- \frac{1}{4}$ .

[6]

Markscheme

(as $\lim_{x \to 0} x^{2} = 0$ , the indeterminate form $\frac{0}{0}$ is required for the limit to exist)

$\Rightarrow \lim_{x \to 0} (arctan (\cos x) - k) = 0$ M1

$arctan 1 - k = 0 (k = arctan 1)$ A1

so $k = \frac{π}{4}$ AG

Note: Award M1A0 for using $k = \frac{π}{4}$ to show the limit is $\frac{0}{0}$ .

[2 marks]

$\lim_{x \to 0} \frac{arctan (\cos x) - \frac{π}{4}}{x^{2}} (= \frac{0}{0})$

$= \lim_{x \to 0} \frac{\frac{- \sin x}{1 + \cos^{2} x}}{2 x}$ A1A1

Note: Award A1 for a correct numerator and A1 for a correct denominator.

recognises to apply l’Hôpital’s rule again (M1)

$= \lim_{x \to 0} \frac{\frac{- \sin x}{1 + \cos^{2} x}}{2 x} (= \frac{0}{0})$

Note: Award M0 if their limit is not the indeterminate form $\frac{0}{0}$ .

EITHER

$= \lim_{x \to 0} \frac{\frac{- \cos x (1 + \cos^{2} x) - 2 \sin^{2} x \cos x}{{(1 + \cos^{2} x)}^{2}}}{2}$ A1A1

Note: Award A1 for a correct first term in the numerator and A1 for a correct second term in the numerator.

$\lim_{x \to 0} \frac{- \cos x}{2 (1 + \cos^{2} x) - 4 x \sin x \cos x}$ A1A1

Note: Award A1 for a correct numerator and A1 for a correct denominator.

THEN

substitutes $x = 0$ into the correct expression to evaluate the limit A1

Note: The final A1 is dependent on all previous marks.

$= - \frac{1}{4}$ AG

[6 marks]

Examiners report

Part (a) Many candidates recognised the indeterminate form and provided a nice algebraic proof. Some verified by substituting the given value. Therefore, there is a need to teach the candidates the difference between proof and verification. Only a few candidates were able to give a complete 'show that' proof.

Part (b) Many candidates realised that they needed to apply the L'Hôpital's rule twice. There were many mistakes in differentiation using the chain rule. Not all candidates clearly showed the final substitution.

[N/A]

Given that a $\times$ b $=$ b $\times$ c $\ne$ 0 prove that a $+$ c $=$ sb where s is a scalar.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

a $\times$ b = b $\times$ c

(a $\times$ b) $-$ (b $\times$ c) = 0

(a $\times$ b) + (c $\times$ b) = 0 M1A1

(a + c) $\times$ b = 0 A1

(a + c) is parallel to b $\Rightarrow$ a + c = sb R1AG

Note: Condone absence of arrows, underlining, or other otherwise “correct” vector notation throughout this question.

Note: Allow “is in the same direction to”, for the final R mark.

METHOD 2

a $\times$ b = b $\times$ c $\Rightarrow \left( {\begin{array}{*{20}{c}} {{a_2}{b_3} - {a_3}{b_2}} \\ {{a_3}{b_1} - {a_1}{b_3}} \\ {{a_1}{b_2} - {a_2}{b_1}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{b_2}{c_3} - {b_3}{c_2}} \\ {{b_3}{c_1} - {b_1}{c_3}} \\ {{b_1}{c_2} - {b_2}{c_1}} \end{array}} \right)$ M1A1

${a_2}{b_3} - {a_3}{b_2} = {b_2}{c_3} - {b_3}{c_2} \Rightarrow {b_3}({a_2} + {c_2}) = {b_2}({a_3} + {c_3})$

${a_3}{b_1} - {a_1}{b_3} = {b_3}{c_1} - {b_1}{c_3} \Rightarrow {b_1}({a_3} + {c_3}) = {b_3}({a_1} + {c_1})$

${a_1}{b_2} - {a_2}{b_1} = {b_1}{c_2} - {b_2}{c_1} \Rightarrow {b_2}({a_1} + {c_1}) = {b_1}({a_2} + {c_2})$

$\frac{{({a_1} + {c_1})}}{{{b_1}}} = \frac{{({a_2} + {c_2})}}{{{b_2}}} = \frac{{({a_3} + {c_3})}}{{{b_3}}} = s$ A1

$\Rightarrow {a_1} + {c_1} = s{b_1}$

$\Rightarrow {a_2} + {c_2} = s{b_2}$

$\Rightarrow {a_3} + {c_3} = s{b_3}$

$\Rightarrow \left( {\begin{array}{*{20}{c}} {{a_1}} \\ {{a_2}} \\ {{a_3}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{c_1}} \\ {{c_2}} \\ {{c_3}} \end{array}} \right) = s\left( {\begin{array}{*{20}{c}} {{b_1}} \\ {{b_2}} \\ {{b_3}} \end{array}} \right)$ A1

$\Rightarrow$ a + c = sb AG

[4 marks]

Examiners report

[N/A]

Two ships, A and B , are observed from an origin O. Relative to O, their position vectors at time t hours after midday are given by

r_A = $\left( {\begin{array}{*{20}{c}} 4 \\ 3 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 5 \\ 8 \end{array}} \right)$

r_B = $\left( {\begin{array}{*{20}{c}} 7 \\ { - 3} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 0 \\ {12} \end{array}} \right)$

where distances are measured in kilometres.

Find the minimum distance between the two ships.

Markscheme

attempting to find r_B − r_A for example (M1)

r_B − r_A = $\left( {\begin{array}{*{20}{c}} 3 \\ { - 6} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} { - 5} \\ 4 \end{array}} \right)$

attempting to find |r_B − r_A| M1

distance $d\left( t \right) = \sqrt {{{\left( {3 - 5t} \right)}^2} + {{\left( {4t - 6} \right)}^2}} \left( { = \sqrt {41{t^2} - 78t + 45} } \right)$ A1

using a graph to find the $d$ − coordinate of the local minimum M1

the minimum distance between the ships is 2.81 (km) $\left( { = \frac{{11\sqrt {41} }}{{41}}\,\left( {{\text{km}}} \right)} \right)$ A1

[5 marks]

Examiners report

[N/A]

In a triangle ${\text{ABC, AB}} = 4{\text{ cm, BC}} = 3{\text{ cm}}$ and ${\rm{B\hat AC}} = \frac{\pi }{9}$ .

Use the cosine rule to find the two possible values for AC.

[5]

Find the difference between the areas of the two possible triangles ABC.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

let ${\text{AC}} = x$

${3^2} = {x^2} + {4^2} - 8x\cos \frac{\pi }{9}$ M1A1

attempting to solve for $x$ (M1)

$x = 1.09,{\text{ }}6.43$ A1A1

METHOD 2

let ${\text{AC}} = x$

using the sine rule to find a value of $C$ M1

${4^2} = {x^2} + {3^2} - 6x\cos (152.869 \ldots ^\circ ) \Rightarrow x = 1.09$ (M1)A1

${4^2} = {x^2} + {3^2} - 6x\cos (27.131 \ldots ^\circ ) \Rightarrow x = 6.43$ (M1)A1

METHOD 3

let ${\text{AC}} = x$

using the sine rule to find a value of $B$ and a value of $C$ M1

obtaining $B = 132.869 \ldots ^\circ ,{\text{ }}7.131 \ldots ^\circ$ and $C = 27.131 \ldots ^\circ ,{\text{ }}152.869 \ldots ^\circ$ A1

$(B = 2.319 \ldots ,{\text{ }}0.124 \ldots$ and $C = 0.473 \ldots ,{\text{ }}2.668 \ldots )$

attempting to find a value of $x$ using the cosine rule (M1)

$x = 1.09,{\text{ }}6.43$ A1A1

Note: Award M1A0(M1)A1A0 for one correct value of $x$

[5 marks]

$\frac{1}{2} \times 4 \times 6.428 \ldots \times \sin \frac{\pi }{9}$ and $\frac{1}{2} \times 4 \times 1.088 \ldots \times \sin \frac{\pi }{9}$ (A1)

( $4.39747 \ldots$ and $0.744833 \ldots$ )

let $D$ be the difference between the two areas

$D = \frac{1}{2} \times 4 \times 6.428 \ldots \times \sin \frac{\pi }{9} - \frac{1}{2} \times 4 \times 1.088 \ldots \times \sin \frac{\pi }{9}$ (M1)

$(D = 4.39747 \ldots - 0.744833 \ldots )$

$= 3.65{\text{ (c}}{{\text{m}}^2})$ A1

[3 marks]

Examiners report

[N/A]

Two boats $A$ and $B$ travel due north.

Initially, boat $B$ is positioned $50$ metres due east of boat $A$ .

The distances travelled by boat $A$ and boat $B$ , after $t$ seconds, are $x$ metres and $y$ metres respectively. The angle $θ$ is the radian measure of the bearing of boat $B$ from boat $A$ . This information is shown on the following diagram.

Show that $y = x + 50 cot θ$ .

[1]

At time $T$ , the following conditions are true.

Boat $B$ has travelled $10$ metres further than boat $A$ .
Boat $B$ is travelling at double the speed of boat $A$ .
The rate of change of the angle $θ$ is $- 0.1$ radians per second.

Find the speed of boat $A$ at time $T$ .

[6]

Markscheme

$\tan θ = \frac{50}{y - x}$ OR $cot θ = \frac{y - x}{50}$ A1

$y = x + 50 cot θ$ AG

Note: $y - x$ may be identified as a length on a diagram, and not written explicitly.

[1 mark]

attempt to differentiate with respect to $t$ (M1)

$\frac{d y}{d t} = \frac{d x}{d t} - 50 {(cosec θ)}^{2} \frac{d θ}{d t}$ A1

attempt to set speed of $B$ equal to double the speed of $A$ (M1)

$2 \frac{d x}{d t} = \frac{d x}{d t} - 50 {(cosec θ)}^{2} \frac{d θ}{d t}$

$\frac{d x}{d t} = - 50 {(cosec θ)}^{2} \frac{d θ}{d t}$ A1

$θ = arctan 5 (= 1.373 \dots = 78.69 \dots °)$ OR ${cosec}^{2} θ = 1 + {cot}^{2} θ = 1 + {(\frac{1}{5})}^{2} = \frac{26}{25}$ (A1)

Note: This A1 can be awarded independently of previous marks.

$\frac{d x}{d t} = - 50 (\frac{26}{25}) \times - 0.1$

So the speed of boat $A$ is $5.2 ({ms}^{- 1})$ A1

Note: Accept $5.20$ from the use of inexact values.

[6 marks]

Examiners report

[N/A]

This diagram shows a metallic pendant made out of four equal sectors of a larger circle of radius ${\text{OB}} = 9{\text{ cm}}$ and four equal sectors of a smaller circle of radius ${\text{OA}} = 3{\text{ cm}}$ .
The angle ${\text{BOC}} =$ 20°.

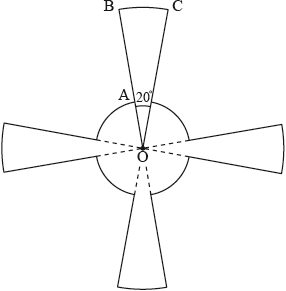
N17/5/MATHL/HP2/ENG/TZ0/03

Find the area of the pendant.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

area = (four sector areas radius 9) + (four sector areas radius 3) (M1)

$= 4\left( {\frac{1}{2}{9^2}\frac{\pi }{9}} \right) + 4\left( {\frac{1}{2}{3^2}\frac{{7\pi }}{{18}}} \right)$ (A1)(A1)

$= 18\pi + 7\pi$

$= 25\pi {\text{ }}( = 78.5{\text{ c}}{{\text{m}}^2})$ A1

METHOD 2

area =

(area of circle radius 3) + (four sector areas radius 9) – (four sector areas radius 3) (M1)

$\pi {3^2} + 4\left( {\frac{1}{2}{9^2}\frac{\pi }{9}} \right) - 4\left( {\frac{1}{2}{3^2}\frac{\pi }{9}} \right)$ (A1)(A1)

Note: Award A1 for the second term and A1 for the third term.

$= 9\pi + 18\pi - 2\pi$

$= 25\pi {\text{ }}( = {\text{ }}78.5{\text{ c}}{{\text{m}}^2})$ A1

Note: Accept working in degrees.

[4 marks]

Examiners report

[N/A]

Find the Cartesian equation of plane Π containing the points ${\text{A}}\left( {6,{\text{ }}2,{\text{ }}1} \right)$ and ${\text{B}}\left( {3,{\text{ }} - 1,{\text{ }}1} \right)$ and perpendicular to the plane $x + 2y - z - 6 = 0$ .

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1

$\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} { - 3} \\ { - 3} \\ 0 \end{array}} \right)$ (A1)

$\left( {\begin{array}{*{20}{c}} { - 3} \\ { - 3} \\ 0 \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ { - 1} \end{array}} \right)$ M1A1

$= \left( {\begin{array}{*{20}{c}} 3 \\ { - 3} \\ { - 3} \end{array}} \right)$ A1

$x - y - z = k$ M1

$k = 3$ equation of plane Π is $x - y - z = 3$ or equivalent A1

METHOD 2

let plane Π be $ax + by + cz = d$

attempt to form one or more simultaneous equations: M1

$a + 2b - c = 0$ (1) A1

$6a + 2b + c = d$ (2)

$3a - b + c = d$ (3) A1

Note: Award second A1 for equations (2) and (3).

attempt to solve M1

EITHER

using GDC gives $a = \frac{d}{3},{\text{ }}b = - \frac{d}{3},{\text{ }}c = - \frac{d}{3}$ (A1)

equation of plane Π is $x - y - z = 3$ or equivalent A1

row reduction M1

equation of plane Π is $x - y - z = 3$ or equivalent A1

[6 marks]

Examiners report

[N/A]

Find the acute angle between the planes with equations $x + y + z = 3$ and $2x - z = 2$ .

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

n $_1 = \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 1 \end{array}} \right)$ and n $_2 = \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ { - 1} \end{array}} \right)$ (A1)(A1)

EITHER

$\theta = \arccos \left( {\frac{{{n_1} \bullet {n_2}}}{{\left| {{n_1}} \right|\left| {{n_2}} \right|}}} \right)\left( {\cos \theta = \frac{{{n_1} \bullet {n_2}}}{{\left| {{n_1}} \right|\left| {{n_2}} \right|}}} \right)$ (M1)

$= \arccos \left( {\frac{{2 + 0 - 1}}{{\sqrt 3 \sqrt 5 }}} \right)\left( {\cos \theta = \frac{{2 + 0 - 1}}{{\sqrt 3 \sqrt 5 }}} \right)$ (A1)

$= \arccos \left( {\frac{1}{{\sqrt {15} }}} \right)\left( {\cos \theta = \frac{1}{{\sqrt {15} }}} \right)$

$\theta = \arcsin \left( {\frac{{\left| {{n_1} \times {n_2}} \right|}}{{\left| {{n_1}} \right|\left| {{n_2}} \right|}}} \right)\left( {\sin \theta = \frac{{\left| {{n_1} \times {n_2}} \right|}}{{\left| {{n_1}} \right|\left| {{n_2}} \right|}}} \right)$ (M1)

$= \arcsin \left( {\frac{{\sqrt {14} }}{{\sqrt 3 \sqrt 5 }}} \right)\left( {\sin \theta = \frac{{\sqrt {14} }}{{\sqrt 3 \sqrt 5 }}} \right)$ (A1)

$= \arcsin \left( {\frac{{\sqrt {14} }}{{\sqrt {15} }}} \right)\left( {\sin \theta = \frac{{\sqrt {14} }}{{\sqrt {15} }}} \right)$

THEN

$= 75.0^\circ {\text{ (or 1.31)}}$ A1

[5 marks]

Examiners report

[N/A]

Boat A is situated 10km away from boat B, and each boat has a marine radio transmitter on board. The range of the transmitter on boat A is 7km, and the range of the transmitter on boat B is 5km. The region in which both transmitters can be detected is represented by the shaded region in the following diagram. Find the area of this region.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

use of cosine rule (M1)

CÂB = arccos $\left( {\frac{{49 + 100 - 25}}{{2 \times 7 \times 10}}} \right) = 0.48276 \ldots \left( { = 27.660 \ldots ^\circ } \right)$ (A1)

C $\mathop {\text{B}}\limits^ \wedge$ A = arccos $\left( {\frac{{25 + 100 - 49}}{{2 \times 5 \times 10}}} \right) = 0.70748 \ldots \left( { = 40.535 \ldots ^\circ } \right)$ (A1)

attempt to subtract triangle area from sector area (M1)

area $= \frac{1}{2} \times 49\left( {2{\text{C}}\mathop {\text{A}}\limits^ \wedge {\text{B}} - {\text{sin}}\,{\text{2C}}\mathop {\text{A}}\limits^ \wedge {\text{B}}} \right)\, + \frac{1}{2} \times 25\left( {2{\text{C}}\mathop {\text{B}}\limits^ \wedge {\text{A}} - {\text{sin}}\,{\text{2C}}\mathop {\text{B}}\limits^ \wedge {\text{A}}} \right)$

= 3.5079… + 5.3385… (A1)

Note: Award this A1 for either of these two values.

= 8.85 (km²) A1

Note: Accept all answers that round to 8.8 or 8.9.

[6 marks]

Examiners report

[N/A]