IB Questionbank

User interface language: English | Español

SL Paper 2

The height of water, in metres, in Dungeness harbour is modelled by the function $H (t) = a \sin (b (t - c)) + d$ , where $t$ is the number of hours after midnight, and $a, b, c$ and $d$ are constants, where $a > 0, b > 0$ and $c > 0$ .

The following graph shows the height of the water for $13$ hours, starting at midnight.

The first high tide occurs at $04 : 30$ and the next high tide occurs $12$ hours later. Throughout the day, the height of the water fluctuates between $2.2 m$ and $6.8 m$ .

All heights are given correct to one decimal place.

Show that $b = \frac{π}{6}$ .

[1]

Find the value of $a$ .

[2]

Find the value of $d$ .

[2]

Find the smallest possible value of $c$ .

[3]

Find the height of the water at $12 : 00$ .

[2]

Determine the number of hours, over a 24-hour period, for which the tide is higher than $5$ metres.

[3]

Markscheme

$12 = \frac{2 π}{b}$ OR $b = \frac{2 π}{12}$ A1

$b = \frac{π}{6}$ AG

[1 mark]

$a = \frac{6.8 - 2.2}{2}$ OR $a = \frac{max - min}{2}$ (M1)

$= 2.3 (m)$ A1

[2 marks]

$d = \frac{6.8 + 2.2}{2}$ OR $d = \frac{max + min}{2}$ (M1)

$= 4.5 (m)$ A1

[2 marks]

METHOD 1

substituting $t = 4.5$ and $H = 6.8$ for example into their equation for $H$ (A1)

$6.8 = 2.3 \sin (\frac{π}{6} (4.5 - c)) + 4.5$

attempt to solve their equation (M1)

$c = 1.5$ A1

METHOD 2

using horizontal translation of $\frac{12}{4}$ (M1)

$4.5 - c = 3$ (A1)

$c = 1.5$ A1

METHOD 3

$H' (t) = (2.3) (\frac{π}{6}) \cos (\frac{π}{6} (t - c))$ (A1)

attempts to solve their $H' (4.5) = 0$ for $c$ (M1)

$(2.3) (\frac{π}{6}) \cos (\frac{π}{6} (4.5 - c)) = 0$

$c = 1.5$ A1

[3 marks]

attempt to find $H$ when $t = 12$ or $t = 0$ , graphically or algebraically (M1)

$H = 2.87365 \dots$

$H = 2.87 (m)$ A1

[2 marks]

attempt to solve $5 = 2.3 \sin (\frac{π}{6} (t - 1.5)) + 4.5$ (M1)

times are $t = 1.91852 \dots$ and $t = 7.08147 \dots, (t = 13.9185 \dots, t = 19.0814 \dots)$ (A1)

total time is $2 \times (7.081 \dots - 1.919 \dots)$

$10.3258 \dots$

$= 10.3$ (hours) A1

Note: Accept $10$ .

[3 marks]

Examiners report

[N/A]

OAB is a sector of the circle with centre O and radius $r$ , as shown in the following diagram.

The angle AOB is $\theta$ radians, where $0 < \theta < \frac{\pi }{2}$ .

The point C lies on OA and OA is perpendicular to BC.

Show that ${\text{OC}} = r\,{\text{cos}}\,\theta$ .

[1]

Find the area of triangle OBC in terms of $r$ and θ.

[2]

Given that the area of triangle OBC is $\frac{3}{5}$ of the area of sector OAB, find θ.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

${\text{cos}}\,\theta = \frac{{{\text{OC}}}}{r}$ A1

${\text{OC}} = r\,{\text{cos}}\,\theta$ AG N0

[1 mark]

valid approach (M1)

eg $\frac{1}{2}{\text{OC}} \times {\text{OB}}\,{\text{sin}}\,\theta$ , ${\text{BC}} = r\,{\text{sin}}\,\theta$ , $\frac{1}{2}r\,{\text{cos}}\,\theta \times {\text{BC}}$ , $\frac{1}{2}r\,{\text{sin}}\,\theta \times {\text{OC}}$

area $= \frac{1}{2}{r^2}\,{\text{sin}}\,\theta \,{\text{cos}}\,\theta$ $\left( { = \frac{1}{4}{r^2}\,{\text{sin}}\left( {2\theta } \right)} \right)$ (must be in terms of $r$ and θ) A1 N2

[2 marks]

valid attempt to express the relationship between the areas (seen anywhere) (M1)

eg OCB = $\frac{3}{5}$ OBA , $\frac{1}{2}{r^2}\,{\text{sin}}\,\theta \,{\text{cos}}\,\theta = \frac{3}{5} \times \frac{1}{2}{r^2}\theta$ , $\frac{1}{4}{r^2}\,{\text{sin}}\,2\theta = \frac{3}{{10}}{r^2}\theta$

correct equation in terms of θ only A1

eg ${\text{sin}}\,\theta \,{\text{cos}}\,\theta = \frac{3}{5}\theta$ , $\frac{1}{4}{\text{sin}}\,2\theta = \frac{3}{{10}}\theta$

valid attempt to solve their equation (M1)

eg sketch, −0.830017, 0

0.830017

θ = 0.830 A1 N2

Note: Do not award final A1 if additional answers given.

[4 marks]

Examiners report

[N/A]

Consider a function $f$ , such that $f(x) = 5, 8\,{\text{sin}}\left( {\frac{\pi }{6}\left( {x + 1} \right)} \right) + b$ , 0 ≤ $x$ ≤ 10, $b \in \mathbb{R}$ .

The function $f$ has a local maximum at the point (2, 21.8) , and a local minimum at (8, 10.2).

A second function $g$ is given by $g(x) = p\,{\text{sin}}\left( {\frac{{2\pi }}{9}\left( {x - 3.75} \right)} \right) + q$ , 0 ≤ $x$ ≤ 10; $p$ , $q \in \mathbb{R}$ .

The function $g$ passes through the points (3, 2.5) and (6, 15.1).

Find the period of $f$ .

[2]

Find the value of $b$ .

[2]

b.i.

Hence, find the value of $f$ (6).

[2]

b.ii.

Find the value of $p$ and the value of $q$ .

[5]

Find the value of $x$ for which the functions have the greatest difference.

[2]

Markscheme

correct approach A1

eg $\frac{\pi }{6} = \frac{{2\pi }}{{period}}$ (or equivalent)

period = 12 A1

[2 marks]

valid approach (M1)

eg $\frac{{{\text{max}} + {\text{min}}}}{2}\,\,b = {\text{max}} - {\text{amplitude}}$

$\frac{{21.8 + 10.2}}{2}$ , or equivalent

$b$ = 16 A1

[2 marks]

b.i.

attempt to substitute into their function (M1)

$5.8\,{\text{sin}}\left( {\frac{\pi }{6}\left( {6 + 1} \right)} \right) + 16$

$f$ (6) = 13.1 A1

[2 marks]

b.ii.

valid attempt to set up a system of equations (M1)

two correct equations A1

$p\,{\text{sin}}\left( {\frac{{2\pi }}{9}\left( {3 - 3.75} \right)} \right) + q = 2.5$ , $p\,{\text{sin}}\left( {\frac{{2\pi }}{9}\left( {6 - 3.75} \right)} \right) + q = 15.1$

valid attempt to solve system (M1)

$p$ = 8.4; $q$ = 6.7 A1A1

[5 marks]

attempt to use $\left| {f(x) - g(x)} \right|$ to find maximum difference (M1)

$x$ = 1.64 A1

[2 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

A water container is made in the shape of a cylinder with internal height $h$ cm and internal base radius $r$ cm.

N16/5/MATSD/SP2/ENG/TZ0/06

The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.

The volume of the water container is $0.5{\text{ }}{{\text{m}}^3}$ .

The water container is designed so that the area to be coated is minimized.

One can of water-resistant material coats a surface area of $2000{\text{ c}}{{\text{m}}^2}$ .

Write down a formula for $A$ , the surface area to be coated.

[2]

Express this volume in ${\text{c}}{{\text{m}}^3}$ .

[1]

Write down, in terms of $r$ and $h$ , an equation for the volume of this water container.

[1]

Show that $A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ .

[2]

Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .

[3]

Using your answer to part (e), find the value of $r$ which minimizes $A$ .

[3]

Find the value of this minimum area.

[2]

Find the least number of cans of water-resistant material that will coat the area in part (g).

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$(A = ){\text{ }}\pi {r^2} + 2\pi rh$ (A1)(A1)

Note: Award (A1) for either $\pi {r^2}$ OR $2\pi rh$ seen. Award (A1) for two correct terms added together.

[2 marks]

$500\,000$ (A1)

Notes: Units not required.

[1 mark]

$500\,000 = \pi {r^2}h$ (A1)(ft)

Notes: Award (A1)(ft) for $\pi {r^2}h$ equating to their part (b).

Do not accept unless $V = \pi {r^2}h$ is explicitly defined as their part (b).

[1 mark]

$A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)$ (A1)(ft)(M1)

Note: Award (A1)(ft) for their ${\frac{{500\,000}}{{\pi {r^2}}}}$ seen.

Award (M1) for correctly substituting only ${\frac{{500\,000}}{{\pi {r^2}}}}$ into a correct part (a).

Award (A1)(ft)(M1) for rearranging part (c) to $\pi rh = \frac{{500\,000}}{r}$ and substituting for $\pi rh$ in expression for $A$ .

$A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ (AG)

Notes: The conclusion, $A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ , must be consistent with their working seen for the (A1) to be awarded.

Accept ${10^6}$ as equivalent to ${1\,000\,000}$ .

[2 marks]

$2\pi r - \frac{{{\text{1}}\,{\text{000}}\,{\text{000}}}}{{{r^2}}}$ (A1)(A1)(A1)

Note: Award (A1) for $2\pi r$ , (A1) for $\frac{1}{{{r^2}}}$ or ${r^{ - 2}}$ , (A1) for $- {\text{1}}\,{\text{000}}\,{\text{000}}$ .

[3 marks]

$2\pi r - \frac{{1\,000\,000}}{{{r^2}}} = 0$ (M1)

Note: Award (M1) for equating their part (e) to zero.

${r^3} = \frac{{1\,000\,000}}{{2\pi }}$ OR $r = \sqrt[3]{{\frac{{1\,000\,000}}{{2\pi }}}}$ (M1)

Note: Award (M1) for isolating $r$ .

sketch of derivative function (M1)

with its zero indicated (M1)

$(r = ){\text{ }}54.2{\text{ }}({\text{cm}}){\text{ }}(54.1926 \ldots )$ (A1)(ft)(G2)

[3 marks]

$\pi {(54.1926 \ldots )^2} + \frac{{1\,000\,000}}{{(54.1926 \ldots )}}$ (M1)

Note: Award (M1) for correct substitution of their part (f) into the given equation.

$= 27\,700{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}(27\,679.0 \ldots )$ (A1)(ft)(G2)

[2 marks]

$\frac{{27\,679.0 \ldots }}{{2000}}$ (M1)

Note: Award (M1) for dividing their part (g) by 2000.

$= 13.8395 \ldots$ (A1)(ft)

Notes: Follow through from part (g).

14 (cans) (A1)(ft)(G3)

Notes: Final (A1) awarded for rounding up their $13.8395 \ldots$ to the next integer.

[3 marks]

Examiners report

[N/A]

The following diagram shows the graph of $f(x) = a\sin bx + c$ , for $0 \leqslant x \leqslant 12$ .

N16/5/MATME/SP2/ENG/TZ0/10

The graph of $f$ has a minimum point at $(3,{\text{ }}5)$ and a maximum point at $(9,{\text{ }}17)$ .

The graph of $g$ is obtained from the graph of $f$ by a translation of $\left( {\begin{array}{*{20}{c}} k \\ 0 \end{array}} \right)$ . The maximum point on the graph of $g$ has coordinates $(11.5,{\text{ }}17)$ .

The graph of $g$ changes from concave-up to concave-down when $x = w$ .

(i) Find the value of $c$ .

(ii) Show that $b = \frac{\pi }{6}$ .

(iii) Find the value of $a$ .

[6]

(i) Write down the value of $k$ .

(ii) Find $g(x)$ .

[3]

(i) Find $w$ .

(ii) Hence or otherwise, find the maximum positive rate of change of $g$ .

[6]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(i) valid approach (M1)

eg $\,\,\,\,\,$ $\frac{{5 + 17}}{2}$

$c = 11$ A1 N2

(ii) valid approach (M1)

eg $\,\,\,\,\,$ period is 12, per $= \frac{{2\pi }}{b},{\text{ }}9 - 3$

$b = \frac{{2\pi }}{{12}}$ A1

$b = \frac{\pi }{6}$ AG N0

(iii) METHOD 1

valid approach (M1)

eg $\,\,\,\,\,$ $5 = a\sin \left( {\frac{\pi }{6} \times 3} \right) + 11$ , substitution of points

$a = - 6$ A1 N2

METHOD 2

valid approach (M1)

eg $\,\,\,\,\,$ $\frac{{17 - 5}}{2}$ , amplitude is 6

$a = - 6$ A1 N2

[6 marks]

(i) $k = 2.5$ A1 N1

(ii) $g(x) = - 6\sin \left( {\frac{\pi }{6}(x - 2.5)} \right) + 11$ A2 N2

[3 marks]

(i) METHOD 1 Using $g$

recognizing that a point of inflexion is required M1

eg $\,\,\,\,\,$ sketch, recognizing change in concavity

evidence of valid approach (M1)

eg $\,\,\,\,\,$ $g''(x) = 0$ , sketch, coordinates of max/min on ${g'}$

$w = 8.5$ (exact) A1 N2

METHOD 2 Using $f$

recognizing that a point of inflexion is required M1

eg $\,\,\,\,\,$ sketch, recognizing change in concavity

evidence of valid approach involving translation (M1)

eg $\,\,\,\,\,$ $x = w - k$ , sketch, $6 + 2.5$

$w = 8.5$ (exact) A1 N2

(ii) valid approach involving the derivative of $g$ or $f$ (seen anywhere) (M1)

eg $\,\,\,\,\,$ $g'(w),{\text{ }} - \pi \cos \left( {\frac{\pi }{6}x} \right)$ , max on derivative, sketch of derivative

attempt to find max value on derivative M1

eg $\,\,\,\,\,$ $- \pi \cos \left( {\frac{\pi }{6}(8.5 - 2.5)} \right),{\text{ }}f'(6)$ , dot on max of sketch

3.14159

max rate of change $= \pi$ (exact), 3.14 A1 N2

[6 marks]

Examiners report

[N/A]

Let $\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 2 \end{array}} \right)$ .

Find $\left| {\overrightarrow {{\text{AB}}} } \right|$ .

[2]

Let $\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 3 \\ 0 \\ 0 \end{array}} \right)$ . Find ${\rm{B\hat AC}}$ .

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct substitution (A1)

eg $\,\,\,\,\,$ $\sqrt {{4^2} + {1^2} + {2^2}}$

4.58257

$\left| {\overrightarrow {{\text{AB}}} } \right| = \sqrt {21}$ (exact), 4.58 A1 N2

[2 marks]

finding scalar product and $\left| {\overrightarrow {{\text{AC}}} } \right|$ (A1)(A1)

scalar product $= (4 \times 3) + (1 \times 0) + (2 \times 0){\text{ }}( = 12)$

$\left| {\overrightarrow {{\text{AC}}} } \right| = \sqrt {{3^2} + 0 + 0} {\text{ }}( = 3)$

substituting their values into cosine formula (M1)

eg cos B $\hat A$ C ${\text{ = }}\frac{{4 \times 3 + 0 + 0}}{{\sqrt {{3^2}} \times \sqrt {21} }},{\text{ }}\frac{4}{{\sqrt {21} }},{\text{ }}\cos \theta = 0.873$

0.509739 (29.2059°)

${\rm{B\hat AC}} = 0.510$ (29.2°) A1 N2

[4 marks]

Examiners report

[N/A]

Olivia’s house consists of four vertical walls and a sloping roof made from two rectangles. The height, ${\text{CD}}$ , from the ground to the base of the roof is 4.5 m.

The base angles of the roof are ${\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}} = 27^\circ$ and ${\text{A}}\mathop {\text{C}}\limits^ \wedge {\text{B}} = 26^\circ$ .

The house is 10 m long and 5 m wide.

The length ${\text{AC}}$ is approximately 2.84 m.

Olivia decides to put solar panels on the roof. The solar panels are fitted to both sides of the roof.

Each panel is 1.6 m long and 0.95 m wide. All the panels must be arranged in uniform rows, with the shorter edge of each panel parallel to ${\text{AB}}$ or ${\text{AC}}$ . Each panel must be at least 0.3 m from the edge of the roof and the top of the roof, ${\text{AF}}$ .

Olivia estimates that the solar panels will cover an area of 29 m².

Find the length ${\text{AB}}$ , giving your answer to four significant figures.

[5]

Find the total area of the two rectangles that make up the roof.

[3]

Find the maximum number of complete panels that can be fitted to the whole roof.

[3]

Find the percentage error in her estimate.

[3]

Olivia investigates arranging the panels, such that the longer edge of each panel is parallel to ${\text{AB}}$ or ${\text{AC}}$ .

State whether this new arrangement will allow Olivia to fit more solar panels to the roof. Justify your answer.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

180° − 27° − 26° (M1)

Note: Award (M1) for correct working to find angle ${\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}$ or 127 seen.

$\frac{{{\text{AB}}}}{{{\text{sin}}\,26^\circ }} = \frac{5}{{{\text{sin}}\,127^\circ }}$ (M1)(A1)

Note: Award (M1) for substitution into sine rule formula and (A1) for correct substitution.

2.74450 (m) (A1)

( ${\text{AB}}$ =) 2.745 (m) (A1)(ft)(G4)

Note: The final (A1)(ft) is for correctly rounding their unrounded ${\text{AB}}$ to 4 sf. If 2.745 is given as the final answer, the unrounded answer need not be seen, award (M1)(M1)(A1)(A2). For all other answers, the unrounded answer must be seen to an accuracy greater than 4 sf.

Award (G3) for a final answer of 2.74450…(m) with no working. If radians are used then award at most (M1)(M1)(A1)(A0)(A1)(ft) for an answer of 3.920 (m).

[5 marks]

Units are required in this question part.

10 × 2.84 + 10 × 2.74450… (M1)(M1)

Note: Award (M1) for finding their area of each rectangle and (M1) for adding their areas.

10 × (2.84 + 2.74450…) (M1)(M1)

Note: Award (M1) for adding ${\text{AC}}$ and their ${\text{AB}}$ . Award (M1) for multiplying their total area by 10.

55.8 (55.8450…) m² (A1)(ft)(G3)

Note: Follow through from their ${\text{AB}}$ in part (a).

[3 marks]

$\frac{{10 - 2\left( {0.3} \right)}}{{1.6}}$ (M1)

Note: Award (M1) for correct calculation of the number of panels on the long side.

$\frac{{2.745 - 2\left( {0.3} \right)}}{{0.95}}$ OR $\frac{{2.84 - 2\left( {0.3} \right)}}{{0.95}}$ (M1)

Note: Award (M1) for correct calculation of the number of panels on either short side with no further incorrect working.

20 (A1)(ft)(G2)

Note: Follow through from part (a). Do not award (M0)(M1)(A1)(ft).

[3 marks]

20 × 1.6 × 0.95 (= 30.4) (M1)

Note: Award (M1) for their 20 × 1.6 × 0.95 or 30.4 seen. Follow through from their 20 in part (c). Award (M0) if their 20 is not an integer.

$\left| {\frac{{29 - 30.4}}{{30.4}}} \right| \times 100{\text{% }}$ (M1)

Note: Award (M1) for correct substitution of their 30.4 into the percentage error formula. Their 30.4 must be exact.

found. Accept a method in two steps where “×100” is implicit from their answer.

The second (M1) is contingent on the first (M1) being awarded, eg do not award (M0)(M1)(A0).

4.61 (%) (4.60526 (%)) (A1)(ft)(G3)

Note: Follow through from their answer to part (c). Percentage sign is not required.

Award (G2) for an unsupported final answer of 4.61.

[3 marks]

1 × 9 (array) OR 18 (total panels) (R1)(ft)

Note: Award (R1) for one correct array seen (1 × 9) or total number of panels (18). Working is not required, but award (R0) for incorrect working seen. Correct working is as follows. $\left( {\frac{{10 - 0.6}}{{0.95}}{\text{,}}\,\,\frac{{2.84 - 0.6}}{{1.6}}{\text{,}}\,\,\frac{{2.745 - 0.6}}{{1.6}}} \right)$
Reasoning may compare both sides of the roof or just one side; accept correct comparisons with part (c) values. Follow through from their treatment of tolerances in part (c) and maximum number of panels.
Award (R0) for any approach with no clearance or for any method which includes further incorrect working.

No (new arrangement will mean fewer solar panels) (A1)(ft)

Note: Follow through from their maximum number of panels in part (c). Do not award (R0)(A1)(ft).

[2 marks]

Examiners report

[N/A]

A company is designing a new logo. The logo is created by removing two equal segments from a rectangle, as shown in the following diagram.

The rectangle measures $5 cm$ by $4 cm$ . The points $A$ and $B$ lie on a circle, with centre $O$ and radius $2 cm$ , such that $AÔB = θ$ , where $0 < θ < π$ . This information is shown in the following diagram.

Find the area of one of the shaded segments in terms of $θ$ .

[3]

Given that the area of the logo is $13.4 {cm}^{2}$ , find the value of $θ$ .

[3]

Markscheme

valid approach to find area of segment by finding area of sector – area of triangle (M1)

$\frac{1}{2} r^{2} θ - \frac{1}{2} r^{2} \sin θ$

$\frac{1}{2} {(2)}^{2} θ - \frac{1}{2} {(2)}^{2} \sin θ$ (A1)

area $= 2 θ - 2 \sin θ$ A1

[3 marks]

EITHER

area of logo = area of rectangle – area of segments (M1)

$5 \times 4 - 2 \times (2 θ - 2 \sin θ) = 13.4$ (A1)

area of one segment $= \frac{20 - 13.4}{2} (= 3.3)$ (M1)

$2 θ - 2 \sin θ = 3.3$ (A1)

THEN

$θ = 2.35672 \dots$

$θ = 2.36$ (do not accept an answer in degrees) A1

Note: Award (M1)(A1)A0 if there is more than one solution.
Award (M1)(A1FT)A0 if the candidate works in degrees and obtains a final answer of $135.030 \dots$

[3 marks]

Examiners report

The first part of this question proved particularly challenging for many candidates. Most were able to obtain the area of the sector, but then did not recognise that the segment was formed by subtracting the area of the triangle. Those that did, often struggled to find the appropriate triangle area formula to do so.

The second part of the question was generally answered more successfully, although sometimes only one of the segments was subtracted from the whole rectangle. Many candidates who had a correct equation lacked the requisite calculator skills to obtain a solution. Those that had an incorrect expression for the area from part (a), often obtained $20 - 4 θ = 13.4$ . This was a significantly easier equation to solve, and consequently these candidates were not awarded the final A mark for a final answer of $θ = 1.65$ .

[N/A]

Using geometry software, Pedro draws a quadrilateral $ABCD$ . $AB = 8 cm$ and $CD = 9 cm$ . Angle $BAD = 51.5 °$ and angle $ADB = 52.5 °$ . This information is shown in the diagram.

$CE = 7 cm$ , where point $E$ is the midpoint of $BD$ .

Calculate the length of $BD$ .

[3]

Show that angle $EDC = 48.0 °$ , correct to three significant figures.

[4]

Calculate the area of triangle $BDC$ .

[3]

Pedro draws a circle, with centre at point $E$ , passing through point $C$ . Part of the circle is shown in the diagram.

Show that point $A$ lies outside this circle. Justify your reasoning.

[5]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{BD}{\sin 51.5 °} = \frac{8}{\sin 52.5 °}$ (M1)(A1)

Note: Award (M1) for substituted sine rule, (A1) for correct substitution.

$(BD =) 7.89 (cm) (7.89164 \dots)$ (A1)(G2)

Note: If radians are used the answer is $9.58723 \dots$ award at most (M1)(A1)(A0).

[3 marks]

$\cos EDC = \frac{9^{2} + 3.94582 \dots^{2} - 7^{2}}{2 \times 9 \times 3.94582 \dots}$ (A1)(ft)(M1)(A1)(ft)

Note: Award (A1) for $3.94582 \dots$ or $\frac{7.89164 \dots}{2}$ seen, (M1) for substituted cosine rule, (A1)(ft) for correct substitutions.

$(EDC =) 47.9515 \dots °$ (A1)

$48.0 °$ ( $3$ sig figures) (AG)

Note: Both an unrounded answer that rounds to the given answer and the rounded value must be seen for the final (M1) to be awarded.
Award at most (A1)(ft)(M1)(A1)(ft)(A0) if the known angle $48.0 °$ is used to validate the result. Follow through from their $BD$ in part (a).

[4 marks]

Units are required in this question.

$(area =) \frac{1}{2} \times 7.89164 \dots \times 9 \times \sin 48.0 °$ (M1)(A1)(ft)

Note: Award (M1) for substituted area formula. Award (A1) for correct substitution.

$(area =) 26.4 {cm}^{2} (26.3908 \dots)$ (A1)(ft)(G3)

Note: Follow through from part (a).

[3 marks]

${AE}^{2} = 8^{2} + {(3.94582 \dots)}^{2} - 2 \times 8 \times 3.94582 \dots \cos (76 °)$ (A1)(M1)(A1)(ft)

Note: Award (A1) for $76 °$ seen. Award (M1) for substituted cosine rule to find $AE$ , (A1)(ft) for correct substitutions.

$(AE =) 8.02 (cm) (8.01849 \dots)$ (A1)(ft)(G3)

Note: Follow through from part (a).

${AE}^{2} = 9.78424 \dots^{2} + {(3.94582 \dots)}^{2} - 2 \times 9.78424 \dots \times 3.94582 \dots \cos (52.5 °)$ (A1)(M1)(A1)(ft)

Note: Award (A1) for $AD (9.78424 \dots)$ or $76 °$ seen. Award (M1) for substituted cosine rule to find $AE$ (do not award (M1) for cosine or sine rule to find $AD$ ), (A1)(ft) for correct substitutions.

$(AE =) 8.02 (cm) (8.01849 \dots)$ (A1)(ft)(G3)

Note: Follow through from part (a).

$8.02 > 7$ . (A1)(ft)

point $A$ is outside the circle. (AG)

Note: Award (A1) for a numerical comparison of $AE$ and $CE$ . Follow through for the final (A1)(ft) within the part for their $8.02$ . The final (A1)(ft) is contingent on a valid method to find the value of $AE$ .
Do not award the final (A1)(ft) if the (AG) line is not stated.
Do not award the final (A1)(ft) if their point $A$ is inside the circle.

[5 marks]

Examiners report

[N/A]

A Ferris wheel with diameter $110$ metres rotates at a constant speed. The lowest point on the wheel is $10$ metres above the ground, as shown on the following diagram. $P$ is a point on the wheel. The wheel starts moving with $P$ at the lowest point and completes one revolution in $20$ minutes.

The height, $h$ metres, of $P$ above the ground after $t$ minutes is given by $h (t) = a \cos (b t) + c$ , where $a, b, c \in ℝ$ .

Find the values of $a$ , $b$ and $c$ .

Markscheme

amplitude is $\frac{110}{2} = 55$ (A1)

$a = - 55$ A1

$c = 65$ A1

$\frac{2 π}{b} = 20$ OR $- 55 \cos (20 b) + 65 = 10$ (M1)

$b = \frac{π}{10} (= 0.314)$ A1

[5 marks]

Examiners report

[N/A]

The following diagram shows a water wheel with centre $O$ and radius $10$ metres. Water flows into buckets, turning the wheel clockwise at a constant speed.

The height, $h$ metres, of the top of a bucket above the ground $t$ seconds after it passes through point $A$ is modelled by the function

$h (t) = 13 + 8 \cos (\frac{π}{18} t) - 6 \sin (\frac{π}{18} t)$ , for $t \geq 0$ .

A bucket moves around to point $B$ which is at a height of $4.06$ metres above the ground. It takes $k$ seconds for the top of this bucket to go from point $A$ to point $B$ .

The chord $[AB]$ is $17.0$ metres, correct to three significant figures.

Find the height of point $A$ above the ground.

[2]

a.i.

Calculate the number of seconds it takes for the water wheel to complete one rotation.

[2]

a.ii.

Hence find the number of rotations the water wheel makes in one hour.

[2]

a.iii.

Find $k$ .

[3]

Find $A \hat{O} B$ .

[3]

Determine the rate of change of $h$ when the top of the bucket is at $B$ .

[2]

Markscheme

valid approach (M1)

eg $h (0), 13 + 8 \cos (\frac{π}{18} \times 0) - 6 \sin (\frac{π}{18} \times 0), 13 + 8 \times 1 - 6 \times 0$

$21$ (metres) A1 N2

[2 marks]

a.i.

valid approach to find the period (seen anywhere) (M1)

eg $(36, 21)$ , attempt to find two consecutive max/min, $50.3130 - 14.3130$

$\frac{2 π}{\frac{π}{18}}, b = \frac{2 π}{period},$

$36$ (seconds) (exact) A1 N2

[2 marks]

a.ii.

correct approach (A1)

eg $\frac{60 \times 60}{36}, 1.6666$ rotations per minute

$100$ (rotations) A1 N2

[2 marks]

a.iii.

correct substitution into equation (accept the use of $t$ ) (A1)

eg $4.06 = 13 + 8 \cos (\frac{π}{18} \times k) - 6 \sin (\frac{π}{18} \times k)$

valid attempt to solve their equation (M1)

$11.6510$

$11.7$ A1 N3

[3 marks]

METHOD 1

evidence of choosing the cosine rule or sine rule (M1)

eg ${AB}^{2} = {OA}^{2} + {OB}^{2} - 2 \times OA \times OB \cos (A \hat{O} B), \frac{\sin (A \hat{O} B)}{AB} = \frac{\sin (O \hat{A} B)}{OB}$

correct working (A1)

eg $\cos (A \hat{O} B) = \frac{10^{2} + 10^{2} - 17 . 0^{2}}{2 \times 10 \times 10}, - 0.445, \frac{\sin (A \hat{O} B)}{17.0} = \frac{\sin (\frac{π}{2} - \frac{1}{2} A \hat{O} B)}{10},$

$\frac{\sin (O \hat{A} B)}{10} = \frac{\sin (π - 2 \times O \hat{A} B)}{17.0}$

$2.03197, 116.423 °$

$2.03 (116 °)$ A1 N3

METHOD 2

attempt to find the half central angle (M1)

eg $\sin (\frac{1}{2} A \hat{O} B) = \frac{\frac{1}{2} AB}{OA}$

correct working (A1)

eg $2 \times \sin^{- 1} (\frac{8.5}{10})$

$2.03197, 116.423 °$

$2.03 (116 °)$ A1 N3

METHOD 3

valid approach to find fraction of period (M1)

eg $\frac{k}{36}, \frac{11.6510}{36}$

correct approach to find angle (A1)

eg $\frac{k}{36} \times 2 π$

$2.03348, 116.510 °$ ( $2.04203$ using $11.7$ )

$2.03 (117 °)$ A1 N3

[3 marks]

recognizing rate of change is $h'$ (M1)

eg $h' (k), h' (11.6510), 0.782024$

$- 0.782024$ ( $- 0.768662$ from $3 sf$ )

rate of change is $- 0.782 ({ms}^{- 1})$ A1 N2

( $- 0.769 ({ms}^{- 1})$ from $3 sf$ )

[2 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

a.iii.

[N/A]

Two points P and Q have coordinates (3, 2, 5) and (7, 4, 9) respectively.

Let ${\mathop {{\text{PR}}}\limits^ \to }$ = 6i − j + 3k.

Find $\mathop {{\text{PQ}}}\limits^ \to$ .

[2]

a.i.

Find $\left| {\mathop {{\text{PQ}}}\limits^ \to } \right|$ .

[2]

a.ii.

Find the angle between PQ and PR.

[4]

Find the area of triangle PQR.

[2]

Hence or otherwise find the shortest distance from R to the line through P and Q.

[3]

Markscheme

valid approach (M1)

eg (7, 4, 9) − (3, 2, 5) A − B

$\mathop {{\text{PQ}}}\limits^ \to =$ 4i + 2j + 4k $\left( { = \left( \begin{gathered} 4 \hfill \\ 2 \hfill \\ 4 \hfill \\ \end{gathered} \right)} \right)$ A1 N2

[2 marks]

a.i.

correct substitution into magnitude formula (A1)
eg $\sqrt {{4^2} + {2^2} + {4^2}}$

$\left| {\mathop {{\text{PQ}}}\limits^ \to } \right| = 6$ A1 N2

[2 marks]

a.ii.

finding scalar product and magnitudes (A1)(A1)

scalar product = (4 × 6) + (2 × (−1) + (4 × 3) (= 34)

magnitude of PR = $\sqrt {36 + 1 + 9} = \left( {6.782} \right)$

correct substitution of their values to find cos ${\text{Q}}\mathop {\text{P}}\limits^ \wedge {\text{R}}$ M1

eg cos ${\text{Q}}\mathop {\text{P}}\limits^ \wedge {\text{R}}\,\,{\text{ = }}\frac{{24 - 2 + 12}}{{\left( 6 \right) \times \left( {\sqrt {46} } \right)}},\,\,0.8355$

0.581746

${\text{Q}}\mathop {\text{P}}\limits^ \wedge {\text{R}}$ = 0.582 radians or ${\text{Q}}\mathop {\text{P}}\limits^ \wedge {\text{R}}$ = 33.3° A1 N3

[4 marks]

correct substitution (A1)
eg $\frac{1}{2} \times \left| {\mathop {{\text{PQ}}}\limits^ \to } \right| \times \left| {\mathop {{\text{PR}}}\limits^ \to } \right| \times \,\,{\text{sin}}\,P,\,\,\frac{1}{2} \times 6 \times \sqrt {46} \times \,\,{\text{sin}}\,0.582$

area is 11.2 (sq. units) A1 N2

[2 marks]

recognizing shortest distance is perpendicular distance from R to line through P and Q (M1)

eg sketch, height of triangle with base $\left[ {{\text{PQ}}} \right],\,\,\frac{1}{2} \times 6 \times h,\,\,{\text{sin}}\,33.3^\circ = \frac{h}{{\sqrt {46} }}$

correct working (A1)

eg $\frac{1}{2} \times 6 \times d = 11.2,\,\,\left| {\mathop {{\text{PR}}}\limits^ \to } \right| \times \,\,{\text{sin}}\,P,\,\,\sqrt {46} \times \,\,{\text{sin}}\,33.3^\circ$

3.72677

distance = 3.73 (units) A1 N2

[3 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

The Tower of Pisa is well known worldwide for how it leans.

Giovanni visits the Tower and wants to investigate how much it is leaning. He draws a diagram showing a non-right triangle, ABC.

On Giovanni’s diagram the length of AB is 56 m, the length of BC is 37 m, and angle ACB is 60°. AX is the perpendicular height from A to BC.

Giovanni’s tourist guidebook says that the actual horizontal displacement of the Tower, BX, is 3.9 metres.

Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree.

[5]

a.i.

Use Giovanni's diagram to calculate the length of AX.

[2]

a.ii.

Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.

[2]

a.iii.

Find the percentage error on Giovanni’s diagram.

[2]

Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.

Find the angle of elevation of A from D.

[3]

Markscheme

$\frac{{{\text{sin BAC}}}}{{37}} = \frac{{{\text{sin 60}}}}{{56}}$ (M1)(A1)

Note: Award (M1) for substituting the sine rule formula, (A1) for correct substitution.

angle ${\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}$ = 34.9034…° (A1)

Note: Award (A0) if unrounded answer does not round to 35. Award (G2) if 34.9034… seen without working.

angle ${\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}$ = 180 − (34.9034… + 60) (M1)

Note: Award (M1) for subtracting their angle BAC + 60 from 180.

85.0965…° (A1)

85° (AG)

Note: Both the unrounded and rounded value must be seen for the final (A1) to be awarded. If the candidate rounds 34.9034...° to 35° while substituting to find angle ${\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}$ , the final (A1) can be awarded but only if both 34.9034...° and 35° are seen.
If 85 is used as part of the workings, award at most (M1)(A0)(A0)(M0)(A0)(AG). This is the reverse process and not accepted.

a.i.

sin 85… × 56 (M1)

= 55.8 (55.7869…) (m) (A1)(G2)

Note: Award (M1) for correct substitution in trigonometric ratio.

a.ii.

$\sqrt {{{56}^2} - 55.7869{ \ldots ^2}}$ (M1)

Note: Award (M1) for correct substitution in the Pythagoras theorem formula. Follow through from part (a)(ii).

cos(85) × 56 (M1)

Note: Award (M1) for correct substitution in trigonometric ratio.

= 4.88 (4.88072…) (m) (A1)(ft)(G2)

Note: Accept 4.73 (4.72863…) (m) from using their 3 s.f answer. Accept equivalent methods.

[2 marks]

a.iii.

$\left| {\frac{{4.88 - 3.9}}{{3.9}}} \right| \times 100$ (M1)

Note: Award (M1) for correct substitution into the percentage error formula.

= 25.1 (25.1282) (%) (A1)(ft)(G2)

Note: Follow through from part (a)(iii).

[2 marks]

${\text{ta}}{{\text{n}}^{ - 1}}\left( {\frac{{55.7869 \ldots }}{{40.11927 \ldots }}} \right)$ (A1)(ft)(M1)

Note: Award (A1)(ft) for their 40.11927… seen. Award (M1) for correct substitution into trigonometric ratio.

(37 − 4.88072…)² + 55.7869…²

(AC =) 64.3725…

64.3726…² + 8² − 2 × 8 × 64.3726… × cos120

(AD =) 68.7226…

$\frac{{{\text{sin 120}}}}{{68.7226 \ldots }} = \frac{{{\text{sin A}}\mathop {\text{D}}\limits^ \wedge {\text{C}}}}{{64.3725 \ldots }}$ (A1)(ft)(M1)

Note: Award (A1)(ft) for their correct values seen, (M1) for correct substitution into the sine formula.

= 54.3° (54.2781…°) (A1)(ft)(G2)

Note: Follow through from part (a). Accept equivalent methods.

[3 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

a.iii.

[N/A]

Consider the points A(−3, 4, 2) and B(8, −1, 5).

A line L has vector equation $r = \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ { - 5} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { - 2} \\ 2 \end{array}} \right)$ . The point C (5, $y$ , 1) lies on line L.

Find $\overrightarrow {{\text{AB}}}$ .

[2]

a.i.

Find $\left| {\overrightarrow {{\text{AB}}} } \right|$ .

[2]

a.ii.

Find the value of $y$ .

[3]

b.i.

Show that $\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 8 \\ { - 10} \\ { - 1} \end{array}} \right)$ .

[2]

b.ii.

Find the angle between $\overrightarrow {{\text{AB}}}$ and $\overrightarrow {{\text{AC}}}$ .

[5]

Find the area of triangle ABC.

[2]

Markscheme

Note: There may be slight differences in answers, depending on which combination of unrounded values and previous correct 3 sf values the candidates carry through in subsequent parts. Accept answers that are consistent with their working.

valid approach (M1)

eg B − A, AO + OB, $\left( {\begin{array}{*{20}{c}} 8 \\ { - 1} \\ 5 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} { - 3} \\ 4 \\ 2 \end{array}} \right)$

$\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} {11} \\ { - 5} \\ 3 \end{array}} \right)$ A1 N2

[2 marks]

a.i.

correct substitution into formula (A1)

eg $\sqrt {{{11}^2} + {{\left( { - 5} \right)}^2} + {3^2}}$

12.4498

$\left| {\overrightarrow {{\text{AB}}} } \right| = \sqrt {155}$ (exact), 12.4 A1 N2

[2 marks]

a.ii.

valid approach to find $t$ (M1)

eg $\left( {\begin{array}{*{20}{c}} 5 \\ y \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ { - 5} \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 1 \\ { - 2} \\ 2 \end{array}} \right)$ , $5 = 2 + t$ , $1 = - 5 + 2t$

$t = 3$ (seen anywhere) (A1)

attempt to substitute their parameter into the vector equation (M1)

eg $\left( {\begin{array}{*{20}{c}} 5 \\ y \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ { - 5} \end{array}} \right) + 3\left( {\begin{array}{*{20}{c}} 1 \\ { - 2} \\ 2 \end{array}} \right)$ , $3 \cdot \left( { - 2} \right)$

$y = - 6$ A1 N2

[3 marks]

b.i.

correct approach A1

eg $\left( {\begin{array}{*{20}{c}} 5 \\ { - 6} \\ 1 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} { - 3} \\ 4 \\ 2 \end{array}} \right)$ , AO + OC, $c - a$

$\overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 8 \\ { - 10} \\ { - 1} \end{array}} \right)$ AG N0

Note: Do not award A1 in part (ii) unless answer in part (i) is correct and does not result from working backwards.

[2 marks]

b.ii.

finding scalar product and magnitude (A1)(A1)

scalar product = 11 × 8 + −5 × −10 + 3 × −1 (=135)

$\overrightarrow {\left| {{\text{AC}}} \right|} = \sqrt {{8^2} + {{\left( { - 10} \right)}^2} + {{\left( { - 1} \right)}^2}} \,\,\left( { = \sqrt {165} ,\,\,12.8452} \right)$

evidence of substitution into formula (M1)

eg ${\text{cos}}{\mkern 1mu} \theta = \frac{{11 \times 8 + - 5 \times - 10 + 3 \times - 1}}{{\left| {\overrightarrow {{\text{AB}}} } \right| \times \sqrt {{8^2} + {{\left( { - 10} \right)}^2} + {{\left( { - 1} \right)}^2}} }}{\text{,}}\,\,{\text{cos}}{\mkern 1mu} \theta = \frac{{\overrightarrow {{\text{AB}}} \bullet \overrightarrow {{\text{AC}}} }}{{\sqrt {155} \times \sqrt {{8^2} + {{\left( { - 10} \right)}^2} + {{\left( { - 1} \right)}^2}} }}$

correct substitution (A1)

eg ${\text{cos}}\,\theta = \frac{{11 \times 8 + - 5 \times - 10 + 3 \times - 1}}{{\sqrt {155} \times \sqrt {{8^2} + {{\left( { - 10} \right)}^2} + {{\left( { - 1} \right)}^2}} }}$ , ${\text{cos}}\,\theta = \frac{{135}}{{159.921 \ldots }}$ ,

${\text{cos}}\,\theta = 0.844162 \ldots$

0.565795, 32.4177°

${\hat A}$ = 0.566, 32.4° A1 N3

[5 marks]

correct substitution into area formula (A1)

eg $\frac{1}{2} \times \sqrt {155} \times \sqrt {165} \times {\text{sin}}\left( {0.566 \ldots } \right)$ , $\frac{1}{2} \times \sqrt {155 \times 165} \times {\text{sin}}\left( {32.4} \right)$

42.8660

area = 42.9 A1 N2

[2 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

Consider the lines ${L_1}$ and ${L_2}$ with respective equations

${L_1}\,{\text{:}}\,y = - \frac{2}{3}x + 9$ and ${L_2}{\text{:}}\,y = \frac{2}{5}x - \frac{{19}}{5}$ .

A third line, ${L_3}$ , has gradient $- \frac{3}{4}$ .

Find the point of intersection of ${L_1}$ and ${L_2}$ .

[2]

Write down a direction vector for ${L_3}$ .

[1]

${L_3}$ passes through the intersection of ${L_1}$ and ${L_2}$ .

Write down a vector equation for ${L_3}$ .

[2]

Markscheme

valid approach (M1)

eg ${L_1} = {L_2}$ , $x = 12$ , $y = 1$

$\left( {12{\text{, }}1} \right)$ (exact) A1 N2

[2 marks]

$\left( {\begin{array}{*{20}{c}} { - 4} \\ 3 \end{array}} \right)$ (or any multiple of $\left( {\begin{array}{*{20}{c}} { - 4} \\ 3 \end{array}} \right)$ ) A1 N1

[1 mark]

any correct equation in the form r = a + $t$ b (accept any parameter for $t$ ) where
a is a position vector for a point on ${L_1}$ , and b is a scalar multiple of $\left( {\begin{array}{*{20}{c}} { - 4} \\ 3 \end{array}} \right)$ A2 N2

eg r $= \left( {\begin{array}{*{20}{c}} {12} \\ 1 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} { - 4} \\ 3 \end{array}} \right)$

Note: Award A1 for the form a + $t$ b, A1 for the form $L$ = a + $t$ b, A0 for the form r = b + $t$ a.

[2 marks]

Examiners report

[N/A]

A pan, in which to cook a pizza, is in the shape of a cylinder. The pan has a diameter of 35 cm and a height of 0.5 cm.

M17/5/MATSD/SP2/ENG/TZ1/04

A chef had enough pizza dough to exactly fill the pan. The dough was in the shape of a sphere.

The pizza was cooked in a hot oven. Once taken out of the oven, the pizza was placed in a dining room.

The temperature, $P$ , of the pizza, in degrees Celsius, °C, can be modelled by

$P(t) = a{(2.06)^{ - t}} + 19,{\text{ }}t \geqslant 0$

where $a$ is a constant and $t$ is the time, in minutes, since the pizza was taken out of the oven.

When the pizza was taken out of the oven its temperature was 230 °C.

The pizza can be eaten once its temperature drops to 45 °C.

Calculate the volume of this pan.

[3]

Find the radius of the sphere in cm, correct to one decimal place.

[4]

Find the value of $a$ .

[2]

Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.

[2]

Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.

[3]

In the context of this model, state what the value of 19 represents.

[1]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$(V = ){\text{ }}\pi \times {{\text{(17.5)}}^2} \times 0.5$ (A1)(M1)

Notes: Award (A1) for 17.5 (or equivalent) seen.

Award (M1) for correct substitutions into volume of a cylinder formula.

$= 481{\text{ c}}{{\text{m}}^3}{\text{ }}(481.056 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}153.125\pi {\text{ c}}{{\text{m}}^3})$ (A1)(G2)

[3 marks]

$\frac{4}{3} \times \pi \times {r^3} = 481.056 \ldots$ (M1)

Note: Award (M1) for equating their answer to part (a) to the volume of sphere.

${r^3} = \frac{{3 \times 481.056 \ldots }}{{4\pi }}{\text{ }}( = 114.843 \ldots )$ (M1)

Note: Award (M1) for correctly rearranging so ${r^3}$ is the subject.

$r = 4.86074 \ldots {\text{ (cm)}}$ (A1)(ft)(G2)

Note: Award (A1) for correct unrounded answer seen. Follow through from part (a).

$= 4.9{\text{ (cm)}}$ (A1)(ft)(G3)

Note: The final (A1)(ft) is awarded for rounding their unrounded answer to one decimal place.

[4 marks]

$230 = a{(2.06)^0} + 19$ (M1)

Note: Award (M1) for correct substitution.

$a = 211$ (A1)(G2)

[2 marks]

$(P = ){\text{ }}211 \times {(2.06)^{ - 5}} + 19$ (M1)

Note: Award (M1) for correct substitution into the function, $P(t)$ . Follow through from part (c). The negative sign in the exponent is required for correct substitution.

$= 24.7$ (°C) $(24.6878 \ldots$ (°C)) (A1)(ft)(G2)

[2 marks]

$45 = 211 \times {(2.06)^{ - t}} + 19$ (M1)

Note: Award (M1) for equating 45 to the exponential equation and for correct substitution (follow through for their $a$ in part (c)).

$(t = ){\text{ }}2.89711 \ldots$ (A1)(ft)(G1)

$174{\text{ (seconds) }}\left( {173.826 \ldots {\text{ (seconds)}}} \right)$ (A1)(ft)(G2)

Note: Award final (A1)(ft) for converting their ${\text{2.89711}} \ldots$ minutes into seconds.

[3 marks]

the temperature of the (dining) room (A1)

the lowest final temperature to which the pizza will cool (A1)

[1 mark]

Examiners report

[N/A]

The depth of water in a port is modelled by the function $d(t) = p\cos qt + 7.5$ , for $0 \leqslant t \leqslant 12$ , where $t$ is the number of hours after high tide.

At high tide, the depth is 9.7 metres.

At low tide, which is 7 hours later, the depth is 5.3 metres.

Find the value of $p$ .

[2]

Find the value of $q$ .

[2]

Use the model to find the depth of the water 10 hours after high tide.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid approach (M1)

eg $\,\,\,\,\,$ $\frac{{{\text{max}} - {\text{min}}}}{2}$ , sketch of graph, $9.7 = p\cos (0) + 7.5$

$p = 2.2$ A1 N2

[2 marks]

valid approach (M1)

eg $\,\,\,\,\,$ $B = \frac{{2\pi }}{{{\text{period}}}}$ , period is $14,{\text{ }}\frac{{360}}{{14}},{\text{ }}5.3 = 2.2\cos 7q + 7.5$

0.448798

$q = \frac{{2\pi }}{{14}}{\text{ }}\left( {\frac{\pi }{7}} \right)$ , (do not accept degrees) A1 N2

[2 marks]

valid approach (M1)

eg $\,\,\,\,\,$ $d(10),{\text{ }}2.2\cos \left( {\frac{{20\pi }}{{14}}} \right) + 7.5$

7.01045

7.01 (m) A1 N2

[2 marks]

Examiners report

[N/A]

The diagram shows a circle, centre O, with radius 4 cm. Points A and B lie on the circumference of the circle and AÔB = θ , where 0 ≤ θ ≤ $\pi$ .

Find the area of the shaded region, in terms of θ.

[3]

The area of the shaded region is 12 cm². Find the value of θ.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid approach to find area of segment (M1)

eg area of sector – area of triangle, $\frac{1}{2}{r^2}\left( {\theta - {\text{sin}}\theta } \right)$

correct substitution (A1)

eg $\frac{1}{4}{\left( 4 \right)^2}\theta - \frac{1}{2}{\left( 4 \right)^2}{\text{sin}}\theta ,\,\,\frac{1}{2} \times 16\left[ {\theta - {\text{sin}}\theta } \right]$

area = 80 – 8 sinθ, 8(θ – sinθ) A1 N2

[3 marks]

setting their area expression equal to 12 (M1)

eg 12 = 8(θ – sinθ)

2.26717

θ = 2.27 (do not accept an answer in degrees) A2 N3

[3 marks]

Examiners report

[N/A]

A restaurant serves desserts in glasses in the shape of a cone and in the shape of a hemisphere. The diameter of a cone shaped glass is 7.2 cm and the height of the cone is 11.8 cm as shown.

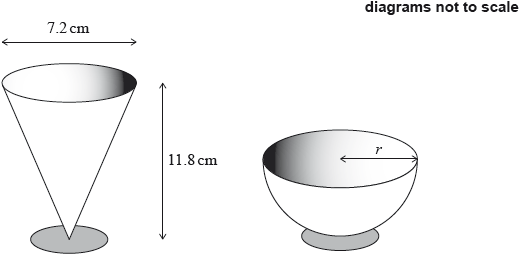
N17/5/MATSD/SP2/ENG/TZ0/06

The volume of a hemisphere shaped glass is $225{\text{ c}}{{\text{m}}^3}$ .

The restaurant offers two types of dessert.

The regular dessert is a hemisphere shaped glass completely filled with chocolate mousse. The cost, to the restaurant, of the chocolate mousse for one regular dessert is $1.89.

The special dessert is a cone shaped glass filled with two ingredients. It is first filled with orange paste to half of its height and then with chocolate mousse for the remaining volume.

N17/5/MATSD/SP2/ENG/TZ0/06.d.e.f

The cost, to the restaurant, of $100{\text{ c}}{{\text{m}}^3}$ of orange paste is $7.42.

A chef at the restaurant prepares 50 desserts; $x$ regular desserts and $y$ special desserts. The cost of the ingredients for the 50 desserts is $111.44.

Show that the volume of a cone shaped glass is $160{\text{ c}}{{\text{m}}^3}$ , correct to 3 significant figures.

[2]

Calculate the radius, $r$ , of a hemisphere shaped glass.

[3]

Find the cost of $100{\text{ c}}{{\text{m}}^3}$ of chocolate mousse.

[2]

Show that there is $20{\text{ c}}{{\text{m}}^3}$ of orange paste in each special dessert.

[2]

Find the total cost of the ingredients of one special dessert.

[2]

Find the value of $x$ .

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$(V = ){\text{ }}\frac{1}{3}\pi {(3.6)^2} \times 11.8$ (M1)

Note: Award (M1) for correct substitution into volume of a cone formula.

$= 160.145 \ldots {\text{ }}({\text{c}}{{\text{m}}^3})$ (A1)

$= 160{\text{ }}({\text{c}}{{\text{m}}^3})$ (AG)

Note: Both rounded and unrounded answers must be seen for the final (A1) to be awarded.

[2 marks]

$\frac{1}{2} \times \frac{4}{3}\pi {r^3} = 225$ (M1)(A1)

Notes: Award (M1) for multiplying volume of sphere formula by $\frac{1}{2}$ (or equivalent).

Award (A1) for equating the volume of hemisphere formula to 225.

$\frac{4}{3}\pi {r^3} = 450$ (A1)(M1)

Notes: Award (A1) for 450 seen, (M1) for equating the volume of sphere formula to 450.

$(r = ){\text{ }}4.75{\text{ }}({\text{cm}}){\text{ }}(4.75380 \ldots )$ (A1)(G2)

[3 marks]

$\frac{{1.89 \times 100}}{{225}}$ (M1)

Note: Award (M1) for dividing 1.89 by 2.25, or equivalent.

$= 0.84$ (A1)(G2)

Note: Accept 84 cents if the units are explicit.

[2 marks]

${r_2} = 1.8$ (A1)

${V_2} = \frac{1}{3}\pi {(1.8)^2} \times 5.9$ (M1)

Note: Award (M1) for correct substitution into volume of a cone formula, but only if the result rounds to 20.

$= 20{\text{ c}}{{\text{m}}^3}$ (AG)

${r_2} = \frac{1}{2}r$ (A1)

${V_2} = {\left( {\frac{1}{2}} \right)^3}160$ (M1)

Notes: Award (M1) for multiplying 160 by ${\left( {\frac{1}{2}} \right)^3}$ . Award (A0)(M1) for $\frac{1}{8} \times 160$ if $\frac{1}{2}$ is not seen.

$= 20{\text{ }}({\text{c}}{{\text{m}}^3})$ (AG)

Notes: Do not award any marks if the response substitutes in the known value $(V = 20)$ to find the radius of the cone.

[2 marks]

$\frac{{20}}{{100}} \times 7.42 + \frac{{140}}{{100}} \times 0.84$ (M1)

Note: Award (M1) for the sum of two correct products.

$ 2.66 (A1)(ft)(G2)

Note: Follow through from part (c).

[2 marks]

$x + y = 50$ (M1)

Note: Award (M1) for correct equation.

$1.89x + 2.66y = 111.44$ (M1)

Note: Award (M1) for setting up correct equation, including their 2.66 from part (e).

$(x = ){\text{ }}28$ (A1)(ft)(G3)

Note: Follow through from part (e), but only if their answer for $x$ is rounded to the nearest positive integer, where $0 < x < 50$ .

Award at most (M1)(M1)(A0) for a final answer of “28, 22”, where the $x$ -value is not clearly defined.

[3 marks]

Examiners report

[N/A]

Abdallah owns a plot of land, near the river Nile, in the form of a quadrilateral ABCD.

The lengths of the sides are ${\text{AB}} = {\text{40 m, BC}} = {\text{115 m, CD}} = {\text{60 m, AD}} = {\text{84 m}}$ and angle ${\rm{B\hat AD}} = 90^\circ$ .

This information is shown on the diagram.

N17/5/MATSD/SP2/ENG/TZ0/03

The formula that the ancient Egyptians used to estimate the area of a quadrilateral ABCD is

${\text{area}} = \frac{{({\text{AB}} + {\text{CD}})({\text{AD}} + {\text{BC}})}}{4}$ .

Abdallah uses this formula to estimate the area of his plot of land.

Show that ${\text{BD}} = 93{\text{ m}}$ correct to the nearest metre.

[2]

Calculate angle ${\rm{B\hat CD}}$ .

[3]

Find the area of ABCD.

[4]

Calculate Abdallah’s estimate for the area.

[2]

d.i.

Find the percentage error in Abdallah’s estimate.

[2]

d.ii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

${\text{B}}{{\text{D}}^2} = {40^2} + {84^2}$ (M1)

Note: Award (M1) for correct substitution into Pythagoras.

Accept correct substitution into cosine rule.

${\text{BD}} = 93.0376 \ldots$ (A1)

$= 93$ (AG)

Note: Both the rounded and unrounded value must be seen for the (A1) to be awarded.

[2 marks]

$\cos C = \frac{{{{115}^2} + {{60}^2} - {{93}^2}}}{{2 \times 115 \times 60}}{\text{ }}({93^2} = {115^2} + {60^2} - 2 \times 115 \times 60 \times \cos C)$ (M1)(A1)

Note: Award (M1) for substitution into cosine formula, (A1) for correct substitutions.

$= 53.7^\circ {\text{ }}(53.6679 \ldots ^\circ )$ (A1)(G2)

[3 marks]

$\frac{1}{2}(40)(84) + \frac{1}{2}(115)(60)\sin (53.6679 \ldots )$ (M1)(M1)(A1)(ft)

Note: Award (M1) for correct substitution into right-angle triangle area. Award (M1) for substitution into area of triangle formula and (A1)(ft) for correct substitution.

$= 4460{\text{ }}{{\text{m}}^2}{\text{ }}(4459.30 \ldots {\text{ }}{{\text{m}}^2})$ (A1)(ft)(G3)

Notes: Follow through from part (b).

[4 marks]

$\frac{{(40 + 60)(84 + 115)}}{4}$ (M1)

Note: Award (M1) for correct substitution in the area formula used by ‘Ancient Egyptians’.

$= 4980{\text{ }}{{\text{m}}^2}{\text{ }}(4975{\text{ }}{{\text{m}}^2})$ (A1)(G2)

[2 marks]

d.i.

$\left| {\frac{{4975 - 4459.30 \ldots }}{{4459.30 \ldots }}} \right| \times 100$ (M1)

Notes: Award (M1) for correct substitution into percentage error formula.

$= 11.6{\text{ }}(\% ){\text{ }}(11.5645 \ldots )$ (A1)(ft)(G2)

Notes: Follow through from parts (c) and (d)(i).

[2 marks]

d.ii.

Examiners report

[N/A]

d.i.

[N/A]

d.ii.

Two straight fences meet at point $A$ and a field lies between them.

A horse is tied to a post, $P$ , by a rope of length $r$ metres. Point $D$ is on one fence and point $E$ is on the other, such that $PD = PE = PA = r$ and $D \hat{P} E = θ$ radians. This is shown in the following diagram.

The length of the arc $DE$ shown in the diagram is $28 m$ .

A new fence is to be constructed between points $B$ and $C$ which will enclose the field, as shown in the following diagram.

Point $C$ is due west of $B$ and $AC = 800 m$ . The bearing of $B$ from $A$ is $195 °$ .

Write down an expression for $r$ in terms of $θ$ .

[1]

Show that the area of the field that the horse can reach is $\frac{392}{θ^{2}} (θ + \sin θ)$ .

[4]

The area of field that the horse can reach is $460 m^{2}$ . Find the value of $θ$ .

[2]

Hence, find the size of $D \hat{A} E$ .

[2]

Find the size of $A \hat{B} C$ .

[2]

e.i.

Find the length of new fence required.

[3]

e.ii.

Markscheme

$r = \frac{28}{θ}$ A1

[1 mark]

recognising sum of area of sector and area of triangle required (M1)

$\frac{1}{2} r^{2} θ + \frac{1}{2} r \times r \times \sin (π - θ) (= \frac{r^{2}}{2} (θ + \sin (π - θ))$ A1

$\sin (π - θ) = \sin θ$ (substitution seen anywhere) A1

$\frac{1}{2} {(\frac{28}{θ})}^{2} θ + \frac{1}{2} {(\frac{28}{θ})}^{2} \sin θ$ OR $\frac{1}{2} {(\frac{28}{θ})}^{2} (θ + \sin θ)$ A1

area $= \frac{392}{θ^{2}} (θ + \sin θ)$ AG

[4 marks]

$\frac{392}{θ^{2}} (θ + \sin θ) = 460$ (M1)

$θ = 1.43917 \dots$

$θ = 1.44$ A1

[2 marks]

$\frac{π - (π - θ)}{2}$ OR $\frac{θ}{2}$ (M1)

$D \hat{A} E = 0.719588 \dots$

$D \hat{A} E = 0.720$ A1

[2 marks]

$A \hat{B} C = 195 - 180 + 90$ (A1)

$= 105 °$ A1

[2 marks]

e.i.

choosing sine rule (M1)

$\frac{BC}{sin D \hat{A} E} = \frac{800}{\sin 105}$ OR $\frac{BC}{sin D \hat{A} E} = \frac{800}{\sin 1.83}$ A1

$BC = 546 (m)$ A1

[2 marks]

e.ii.

Examiners report

[N/A]

e.i.

[N/A]

e.ii.

Note: In this question, distance is in millimetres.

Let $f(x) = x + a\sin \left( {x - \frac{\pi }{2}} \right) + a$ , for $x \geqslant 0$ .

The graph of $f$ passes through the origin. Let ${{\text{P}}_k}$ be any point on the graph of $f$ with $x$ -coordinate $2k\pi$ , where $k \in \mathbb{N}$ . A straight line $L$ passes through all the points ${{\text{P}}_k}$ .

Diagram 1 shows a saw. The length of the toothed edge is the distance AB.

N17/5/MATME/SP2/ENG/TZ0/10.d_01

The toothed edge of the saw can be modelled using the graph of $f$ and the line $L$ . Diagram 2 represents this model.

N17/5/MATME/SP2/ENG/TZ0/10.d_02

The shaded part on the graph is called a tooth. A tooth is represented by the region enclosed by the graph of $f$ and the line $L$ , between ${{\text{P}}_k}$ and ${{\text{P}}_{k + 1}}$ .

Show that $f(2\pi ) = 2\pi$ .

[3]

Find the coordinates of ${{\text{P}}_0}$ and of ${{\text{P}}_1}$ .

[3]

b.i.

Find the equation of $L$ .

[3]

b.ii.

Show that the distance between the $x$ -coordinates of ${{\text{P}}_k}$ and ${{\text{P}}_{k + 1}}$ is $2\pi$ .

[2]

A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.

[6]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

substituting $x = 2\pi$ M1

eg $\,\,\,\,\,$ $2\pi + a\sin \left( {2\pi - \frac{\pi }{2}} \right) + a$

$2\pi + a\sin \left( {\frac{{3\pi }}{2}} \right) + a$ (A1)

$2\pi - a + a$ A1

$f(2\pi ) = 2\pi$ AG N0

[3 marks]

substituting the value of $k$ (M1)

${{\text{P}}_0}(0,{\text{ }}0),{\text{ }}{{\text{P}}_1}(2\pi ,{\text{ }}2\pi )$ A1A1 N3

[3 marks]

b.i.

attempt to find the gradient (M1)

eg $\,\,\,\,\,$ $\frac{{2\pi - 0}}{{2\pi - 0}},{\text{ }}m = 1$

correct working (A1)

eg $\,\,\,\,\,$ $\frac{{y - 2\pi }}{{x - 2\pi }} = 1,{\text{ }}b = 0,{\text{ }}y - 0 = 1(x - 0)$

y = x A1 N3

[3 marks]

b.ii.

subtracting $x$ -coordinates of ${{\text{P}}_{k + 1}}$ and ${{\text{P}}_k}$ (in any order) (M1)

eg $\,\,\,\,\,$ $2(k + 1)\pi - 2k\pi ,{\text{ }}2k\pi - 2k\pi - 2\pi$

correct working (must be in correct order) A1

eg $\,\,\,\,\,$ $2k\pi + 2\pi - 2k\pi ,{\text{ }}\left| {2k\pi - 2(k + 1)\pi } \right|$

distance is $2\pi$ AG N0

[2 marks]

METHOD 1

recognizing the toothed-edge as the hypotenuse (M1)

eg $\,\,\,\,\,$ ${300^2} = {x^2} + {y^2}$ , sketch

correct working (using their equation of $L$ (A1)

eg $\,\,\,\,\,$ ${300^2} = {x^2} + {x^2}$

$x = \frac{{300}}{{\sqrt 2 }}$ (exact), 212.132 (A1)

dividing their value of $x$ by $2\pi {\text{ }}\left( {{\text{do not accept }}\frac{{300}}{{2\pi }}} \right)$ (M1)

eg $\,\,\,\,\,$ $\frac{{212.132}}{{2\pi }}$

33.7618 (A1)

33 (teeth) A1 N2

METHOD 2

vertical distance of a tooth is $2\pi$ (may be seen anywhere) (A1)

attempt to find the hypotenuse for one tooth (M1)

eg $\,\,\,\,\,$ ${x^2} = {(2\pi )^2} + {(2\pi )^2}$

$x = \sqrt {8{\pi ^2}}$ (exact), 8.88576 (A1)

dividing 300 by their value of $x$ (M1)

33.7618 (A1)

33 (teeth) A1 N2

[6 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

A farmer is placing posts at points $A$ , $B$ , and $C$ in the ground to mark the boundaries of a triangular piece of land on his property.

From point $A$ , he walks due west $230$ metres to point $B$ .
From point $B$ , he walks $175$ metres on a bearing of $063 °$ to reach point $C$ .

This is shown in the following diagram.

The farmer wants to divide the piece of land into two sections. He will put a post at point $D$ , which is between $A$ and $C$ . He wants the boundary $BD$ to divide the piece of land such that the sections have equal area. This is shown in the following diagram.

Find the distance from point $A$ to point $C$ .

[4]

Find the area of this piece of land.

[2]

Find $CÂB$ .

[3]

Find the distance from point $B$ to point $D$ .

[5]

Markscheme

$A \hat{B} C = 27 °$ (A1)

attempt to substitute into cosine rule (M1)

$175^{2} + 230^{2} - 2 (175) (230) \cos 27 °$ (A1)

$108.62308 \dots$

$AC = 109 (m)$ A1

[4 marks]

correct substitution into area formula (A1)

$\frac{1}{2} \times 175 \times 230 \times \sin 27 °$

$9136.55 \dots$

area $= 9140 (m^{2})$ A1

[2 marks]

attempt to substitute into sine rule or cosine rule (M1)

$\frac{\sin 27 °}{108.623 \dots} = \frac{\sin \hat{A}}{175}$ OR $\cos A = \frac{{(108.623 \dots)}^{2} + 230^{2} - 175^{2}}{2 \times 108.623 \dots \times 230}$ (A1)

$47.0049 \dots$

$CÂB = 47.0 °$ A1

[3 marks]

METHOD 1

recognizing that for areas to be equal, $AD = DC$ (M1)

$AD = \frac{1}{2} AC = 54.3115 \dots$ A1

attempt to substitute into cosine rule to find $BD$ (M1)

correct substitution into cosine rule (A1)

${BD}^{2} = 230^{2} + 54 . 3115^{2} - 2 (230) (54.3115) \cos 47.0049 °$

$BD = 197.009 \dots$

$BD = 197 (m)$ A1

METHOD 2

correct expressions for areas of triangle $BDA$ and triangle $BCD$ using $BD$ A1

$\frac{1}{2} \times BD \times 230 \times \sin x °$ and $\frac{1}{2} \times BD \times 175 \times \sin (27 - x) °$ OR

$\frac{1}{2} \times BD \times 230 \times \sin (27 - x) °$ and $\frac{1}{2} \times BD \times 175 \times \sin x °$

correct equation in terms of $x$ (A1)

$175 \sin (27 - x) = 230 \sin x$ or $175 \sin x = 230 \sin (27 - x)$

$x = 11.6326 \dots$ or $x = 15.3673 \dots$ (A1)

substituting their value of $x$ into equation to solve for $BD$ (M1)

$\frac{1}{2} \times BD \times 230 \times \sin 11.6326 \dots = \frac{1}{2} \times BD \times 175 \times \sin 15.3673 \dots$ or

$\frac{1}{2} \times BD \times 230 \times \sin 11.6326 \dots = \frac{1}{2} \times 9136.55 \dots$

$BD = 197 (m)$ A1

[5 marks]

Examiners report

Students performed well on parts (a)-(c), correctly applying the cosine rule, the sine formula for area and the sine rule. Part (d) proved challenging. A common error was to falsely assume that segment BD bisected angle ABC.

A significant number of candidates did not have their calculator in degree mode or started in radians and changed to degrees part way through but used answers they had obtained when they were in radian mode. They got answers which were clearly impossible from the diagram, but most did not notice this.

Accuracy was a great problem throughout this question: premature rounding, incorrect rounding, or quoting more figures for the answer than they had used in the calculation.

[N/A]

Let $f\left( x \right) = 12\,\,{\text{cos}}\,x - 5\,\,{\text{sin}}\,x,\,\, - \pi \leqslant x \leqslant 2\pi$ , be a periodic function with $f\left( x \right) = f\left( {x + 2\pi } \right)$

The following diagram shows the graph of $f$ .

There is a maximum point at A. The minimum value of $f$ is −13 .

A ball on a spring is attached to a fixed point O. The ball is then pulled down and released, so that it moves back and forth vertically.

The distance, d centimetres, of the centre of the ball from O at time t seconds, is given by

$d\left( t \right) = f\left( t \right) + 17,\,\,0 \leqslant t \leqslant 5.$

Find the coordinates of A.

[2]

For the graph of $f$ , write down the amplitude.

[1]

b.i.

For the graph of $f$ , write down the period.

[1]

b.ii.

Hence, write $f\left( x \right)$ in the form $p\,\,{\text{cos}}\,\left( {x + r} \right)$ .

[3]

Find the maximum speed of the ball.

[3]

Find the first time when the ball’s speed is changing at a rate of 2 cm s⁻².

[5]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

−0.394791,13

A(−0.395, 13) A1A1 N2

[2 marks]

13 A1 N1

[1 mark]

b.i.

${2\pi }$ , 6.28 A1 N1

[1 mark]

b.ii.

valid approach (M1)

eg recognizing that amplitude is p or shift is r

$f\left( x \right) = 13\,\,{\text{cos}}\,\left( {x + 0.395} \right)$ (accept p = 13, r = 0.395) A1A1 N3

Note: Accept any value of r of the form $0.395 + 2\pi k,\,\,k \in \mathbb{Z}$

[3 marks]

recognizing need for d ′(t) (M1)

eg −12 sin(t) − 5 cos(t)

correct approach (accept any variable for t) (A1)

eg −13 sin(t + 0.395), sketch of d′, (1.18, −13), t = 4.32

maximum speed = 13 (cms⁻¹) A1 N2

[3 marks]

recognizing that acceleration is needed (M1)

eg a(t), d "(t)

correct equation (accept any variable for t) (A1)

eg $a\left( t \right) = - 2,\,\,\left| {\frac{{\text{d}}}{{{\text{d}}t}}\left( {d'\left( t \right)} \right)} \right| = 2,\,\, - 12\,\,{\text{cos}}\,\left( t \right) + 5\,\,{\text{sin}}\,\left( t \right) = - 2$

valid attempt to solve their equation (M1)

eg sketch, 1.33

1.02154

1.02 A2 N3

[5 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

The six blades of a windmill rotate around a centre point $C$ . Points $A$ and $B$ and the base of the windmill are on level ground, as shown in the following diagram.

From point $A$ the angle of elevation of point $C$ is $0.6$ radians.

An observer walks $7$ metres from point $A$ to point $B$ .

The observer keeps walking until he is standing directly under point $C$ . The observer has a height of $1.8$ metres, and as the blades of the windmill rotate, the end of each blade passes $2.5$ metres over his head.

One of the blades is painted a different colour than the others. The end of this blade is labelled point $D$ . The height $h$ , in metres, of point $D$ above the ground can be modelled by the function $h (t) = p \cos (\frac{3 π}{10} t) + q$ , where $t$ is in seconds and $p, q \in ℝ$ . When $t = 0$ , point $D$ is at its maximum height.

Given that point $A$ is $12$ metres from the base of the windmill, find the height of point $C$ above the ground.

[2]

Find the angle of elevation of point $C$ from point $B$ .

[2]

Find the length of each blade of the windmill.

[2]

Find the value of $p$ and the value of $q$ .

[4]

If the observer stands directly under point $C$ for one minute, point $D$ will pass over his head $n$ times.

Find the value of $n$ .

[3]

Markscheme

$\tan 0.6 = \frac{h}{12}$ (M1)

$8.20964 \dots$

$8.21 (m)$ A1

[2 marks]

$\tan B = \frac{8.2096 \dots}{5}$ OR $\tan^{- 1} 1.6419 \dots$ (A1)

$1.02375 \dots$

$1.02$ (radians) (accept $58.7 °$ ) A1

[2 marks]

$x + 1.8 + 2.5 = 8.20964 \dots$ (or equivalent) (A1)

$3.90964 \dots$

$3.91$ ( $m$ ) A1

[2 marks]

METHOD 1

recognition that blade length = amplitude, $p = \frac{max - min}{2}$ (M1)

$p = 3.91$ A1

centre of windmill = vertical shift, $q = \frac{max + min}{2}$ (M1)

$q = 8.21$ A1

METHOD 2

attempting to form two equations in terms of $p$ and $q$ (M1)(M1)

$12.1192 \dots = p \cos (\frac{3 π}{10} \cdot 0) + q, 4.3000 \dots = p \cos (\frac{3 π}{10} \cdot \frac{10}{3}) + q$

$p = 3.91$ A1

$q = 8.21$ A1

[4 marks]

appropriate working towards finding the period (M1)

$period = \frac{2 π}{\frac{3 π}{10}} (= 6.6666 \dots)$

rotations per minute $= \frac{60}{their period}$ (M1)

$n = 9$ (must be an integer) (accept $n = 10$ , $n = 18$ , $n = 19$ ) A1

[3 marks]

Examiners report

[N/A]

The following diagram shows quadrilateral ABCD.

${\text{AB}} = 11\,{\text{cm,}}\,\,{\text{BC}} = 6\,{\text{cm,}}\,\,{\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{D = 100}}^\circ {\text{, and C}}\mathop {\text{B}}\limits^ \wedge {\text{D = 82}}^\circ$

Find DB.

[3]

Find DC.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of choosing sine rule (M1)

eg $\frac{a}{{{\text{sin }}A}} = \frac{b}{{{\text{sin }}B}} = \frac{c}{{{\text{sin }}C}}$

correct substitution (A1)
eg $\frac{{{\text{DB}}}}{{{\text{sin }}59^\circ }} = \frac{{{\text{11}}}}{{{\text{sin }}100^\circ }}$

9.57429

DB = 9.57 (cm) A1 N2

[3 marks]

evidence of choosing cosine rule (M1)

eg ${a^2} = {b^2} + {c^2} - 2bc\,\,{\text{cos}}\,\,\left( A \right),\,\,\,{\text{D}}{{\text{C}}^2} = \,\,{\text{D}}{{\text{B}}^2}{\text{ + B}}{{\text{C}}^2}{\text{ }} - {\text{ 2DB}} \times \,\,{\text{BC}} \times \,{\text{cos}}\,\left( {{\text{D}}\mathop {\text{B}}\limits^ \wedge {\text{C}}} \right)$

correct substitution into RHS (A1)
eg ${9.57^2} + {6^2} - 2 \times 9.57 \times 6 \times \,\,{\text{cos}}\,\,82^\circ ,\,\,\,111.677$

10.5677

DC = 10.6 (cm) A1 N2

[3 marks]

Examiners report

[N/A]

Let $f\left( x \right) = 2\,{\text{sin}}\left( {3x} \right) + 4$ for $x \in \mathbb{R}$ .

Let $g\left( x \right) = 5f\left( {2x} \right)$ .

The function $g$ can be written in the form $g\left( x \right) = 10\,{\text{sin}}\left( {bx} \right) + c$ .

The range of $f$ is $k$ ≤ $f\left( x \right)$ ≤ $m$ . Find $k$ and $m$ .

[3]

Find the range of $g$ .

[2]

Find the value of $b$ and of $c$ .

[3]

c.i.

Find the period of $g$ .

[2]

c.ii.

The equation $g\left( x \right) = 12$ has two solutions where $\pi$ ≤ $x$ ≤ ${\frac{{4\pi }}{3}}$ . Find both solutions.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid attempt to find range (M1)

eg , max = 6 min = 2,

$2\,{\text{sin}}\left( {3 \times \frac{\pi }{6}} \right) + 4$ and $2\,{\text{sin}}\left( {3 \times \frac{\pi }{2}} \right) + 4$ , $2\left( 1 \right) + 4$ and $2\left( { - 1} \right) + 4$ ,

$k = 2$ , $m = 6$ A1A1 N3

[3 marks]

10 ≤ $y$ ≤ 30 A2 N2

[2 marks]

evidence of substitution (may be seen in part (b)) (M1)

eg $5\left( {2\,{\text{sin}}\left( {{\text{3}}\left( {2x} \right)} \right) + 4} \right)$ , ${{\text{3}}\left( {2x} \right)}$

$b = 6$ , $c = 20$ (accept $10\,{\text{sin}}\left( {6x} \right) + 20$ ) A1A1 N3

Note: If no working shown, award N2 for one correct value.

[3 marks]

c.i.

correct working (A1)

eg $\frac{{2\pi }}{b}$

1.04719

$\frac{{2\pi }}{6}\,\,\,\left( { = \frac{\pi }{3}} \right)$ , 1.05 A1 N2

[2 marks]

c.ii.

valid approach (M1)

eg , ${\text{si}}{{\text{n}}^{ - 1}}\left( { - \frac{8}{{10}}} \right){\text{, }}6x = - 0.927{\text{, }} - 0.154549{\text{, }}x = 0.678147$

Note: Award M1 for any correct value for $x$ or $6x$ which lies outside the domain of $f$ .

3.81974, 4.03424

$x = 3.82$ , $x = 4.03$ (do not accept answers in degrees) A1A1 N3

[3 marks]

Examiners report

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

Adam sets out for a hike from his camp at point A. He hikes at an average speed of 4.2 km/h for 45 minutes, on a bearing of 035° from the camp, until he stops for a break at point B.

Adam leaves point B on a bearing of 114° and continues to hike for a distance of 4.6‌ km until he reaches point C.

Adam’s friend Jacob wants to hike directly from the camp to meet Adam at point C .

Find the distance from point A to point B.

[2]

Show that ${\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}$ is 101°.

[2]

b.i.

Find the distance from the camp to point C.

[3]

b.ii.

Find ${\text{B}}\mathop {\text{C}}\limits^ \wedge {\text{A}}$ .

[3]

Find the bearing that Jacob must take to point C.

[3]

Jacob hikes at an average speed of 3.9 km/h.

Find, to the nearest minute, the time it takes for Jacob to reach point C.

[3]

Markscheme

$\frac{{4.2}}{{60}} \times 45$ A1

AB = 3.15 (km) A1

[2 marks]

66° or (180 − 114) A1

35 + 66 A1

${\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}$ = 101° AG

[2 marks]

b.i.

attempt to use cosine rule (M1)

AC² = 3.15² + 4.6² − 2 × 3.15 × 4.6 cos 101° (or equivalent) A1

AC = 6.05 (km) A1

[3 marks]

b.ii.

valid approach to find angle BCA (M1)

eg sine rule

correct substitution into sine rule A1

eg $\frac{{{\text{sin}}\left( {{\text{B}}\mathop {\text{C}}\limits^ \wedge {\text{A}}} \right)}}{{3.15}} = \frac{{{\text{sin}}\,{\text{101}}}}{{6.0507 \ldots }}$

${\text{B}}\mathop {\text{C}}\limits^ \wedge {\text{A}}$ = 30.7° A1

[3 marks]

${\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}$ = 48.267 (seen anywhere) A1

valid approach to find correct bearing (M1)

eg 48.267 + 35

bearing = 83.3° (accept 083°) A1

[3 marks]

attempt to use ${\text{time}} = \frac{{{\text{distance}}}}{{{\text{speed}}}}$ M1

$\frac{{6.0507}}{{3.9}}$ or 0.065768 km/min (A1)

t = 93 (minutes) A1

[3 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

The quadrilateral ABCD represents a park, where ${\text{AB}} = 120{\text{ m}}$ , ${\text{AD}} = 95{\text{ m}}$ and ${\text{DC}} = 100{\text{ m}}$ . Angle DAB is 70° and angle DCB is 110°. This information is shown in the following diagram.

M17/5/MATSD/SP2/ENG/TZ2/04

A straight path through the park joins the points B and D.

A new path, CE, is to be built such that E is the point on BD closest to C.

The section of the park represented by triangle DCE will be used for a charity race. A track will be marked along the sides of this section.

Find the length of the path BD.

[3]

Show that angle DBC is 48.7°, correct to three significant figures.

[3]

Find the area of the park.

[4]

Find the length of the path CE.

[2]

Calculate the total length of the track.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$({\text{B}}{{\text{D}}^2} = ){\text{ }}{95^2} + {120^2} - 2 \times 95 \times 120 \times \cos 70^\circ$ (M1)(A1)

Note: Award (M1) for substituted cosine rule, (A1) for correct substitution.

$({\text{BD}} = ){\text{ }}125{\text{ (m) }}\left( {125.007 \ldots {\text{ (m)}}} \right)$ (A1)(G2)

[3 marks]

$\frac{{\sin {\text{DBC}}}}{{100}} = \frac{{\sin 110^\circ }}{{125.007 \ldots }}$ (M1)(A1)(ft)

Note: Award (M1) for substituted sine rule, (A1)(ft) for correct substitution.

Follow through from their answer to part (a).

$({\text{DBC}} = ){\text{ }}48.7384 \ldots ^\circ$ (A1)(ft)

$({\text{DBC}} = ){\text{ }}48.7^\circ$ (AG)

Notes: Award the final (A1)(ft) only if both their unrounded answer and 48.7° is seen. Follow through from their answer to part (a), only if their unrounded answer rounds to 48.7°.

[3 marks]

$\frac{1}{2} \times 125.007 \ldots \times 100 \times \sin 21.3^\circ + \frac{1}{2} \times 95 \times 120 \times \sin 70^\circ$ (A1)(M1)(M1)

Note: Award (A1) for 21.3° (21.2615…) seen, (M1) for substitution into (at least) one area of triangle formula in the form $\frac{1}{2}ab\sin c$ , (M1) for their correct substitutions and adding the two areas.

$7630{\text{ }}{{\text{m}}^2}{\text{ }}(7626.70 \ldots {{\text{m}}^2})$ (A1)(ft)(G3)

Notes: Follow through from their answers to part (a). Accept $7620{\text{ }}{{\text{m}}^2}{\text{ }}(7622.79 \ldots {{\text{m}}^2})$ from use of 48.7384…

[4 marks]

$({\text{CE}} = ){\text{ }}100 \times \sin 21.3^\circ$ (M1)

$({\text{CE}} = ){\text{ }}36.3{\text{ (m) }}\left( {36.3251 \ldots {\text{ (m)}}} \right)$ (A1)(ft)(G2)

Note: Follow through from their angle 21.3° in part (c). Award (M0)(A0) for halving 110° and/or assuming E is the midpoint of BD in any method seen.

${\text{area of BCD}} = \frac{1}{2}{\text{BD}} \times {\text{CE}}$ (M1)

$({\text{CE}} = ){\text{ }}36.3{\text{ (m) }}\left( {36.3251 \ldots {\text{ (m)}}} \right)$ (A1)(ft)(G2)

Note: Follow through from parts (a) and (c). Award (M0)(A0) for halving 110° and/or assuming E is the midpoint of BD in any method seen.

[2 marks]

$\sqrt {{{100}^2} - 36.3251{ \ldots ^2}} + 100 + 36.3251 \ldots$ (M1)(M1)

Note: Award (M1) for correct use of Pythagoras to find DE (or correct trigonometric equation, $100 \times \cos 21.3$ , to find DE), (M1) for the sum of 100, their DE and their CE.

$229{\text{ (m) }}\left( {229.494 \ldots {\text{ (m)}}} \right)$ (A1)(ft)(G2)

Note: Follow through from part (d). Use of 3 sf values gives an answer of $230{\text{ (m) }}\left( {229.5{\text{ (m)}}} \right)$ .

[3 marks]

Examiners report

[N/A]

An archaeological site is to be made accessible for viewing by the public. To do this, archaeologists built two straight paths from point A to point B and from point B to point C as shown in the following diagram. The length of path AB is 185 m, the length of path BC is 250 m, and angle ${\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}$ is 125°.

The archaeologists plan to build two more straight paths, AD and DC. For the paths to go around the site, angle ${\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{D}}$ is to be made equal to 85° and angle ${\text{B}}\mathop {\text{C}}\limits^ \wedge {\text{D}}$ is to be made equal to 70° as shown in the following diagram.

Find the distance from A to C.

[3]

Find the size of angle ${\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}$ .

[3]

b.i.

Find the size of angle ${\text{C}}\mathop {\text{A}}\limits^ \wedge {\text{D}}$ .

[1]

b.ii.

Find the size of angle ${\text{A}}\mathop {\text{C}}\limits^ \wedge {\text{D}}$ .

[2]

The length of path AD is 287 m.

Find the area of the region ABCD.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

AC² = 185² + 250² − 2 × 185 × 250 × cos(125°) (M1)(A1)

Note: Award (M1) for substitution in the cosine formula; (A1) for correct substitution.

387 (387.015…) (m) (A1)(G2)

Note: If radians are used the answer is 154 (154.471…), award at most (M1)(A1)(A0).

[3 marks]

$\frac{{250}}{{{\text{sin}}\,{\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}}} = \frac{{387.015 \ldots }}{{{\text{sin}}\,\left( {125^\circ } \right)}}$ (M1)(A1)(ft)

${\text{co}}{{\text{s}}^{ - 1}}\left( {\frac{{{{185}^2} + 387.015{ \ldots ^2} - {{250}^2}}}{{2 \times 185 \times 387.015 \ldots }}} \right)$ (M1)(A1)(ft)

Note: Award (M1) for substitution in the sine or cosine formulas; (A1)(ft) for correct substitution.

${\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}} = {\text{31}}{\text{.9}}^\circ$ (31.9478…°) (A1)(ft)(G2)

Note: Follow through from part (a).

[3 marks]

b.i.

(CAD =) 53.1° (53.0521…°) (A1)(ft)

Note: Follow through from their part (b)(i) only if working seen.

[1 mark]

b.ii.

(ACD = ) 70° − (180° − 125° − 31.9478°…) (M1)

Note: Award (M1) for subtracting their angle ${\text{A}}\mathop {\text{C}}\limits^ \wedge {\text{B}}$ from 70°.

(ADC =) 360 − (85 + 70 + 125) = 80

(ACD =) 180 − 80 − 53.0521... (M1)

46.9° (46.9478…°) (A1)(ft)(G2)

Note: Follow through from part (b)(i).

[2 marks]

$\frac{{185 \times 250 \times {\text{sin}}\,\left( {125^\circ } \right)}}{2} + \frac{{287 \times 387.015 \ldots \times {\text{sin}}\,\left( {53.0521 \ldots ^\circ } \right)}}{2}$ (M1)(M1)(M1)

Note: Award (M1) for substitution in the area formula for either triangle; (M1) for correct substitution for both areas; (M1) for adding their two areas;

18942.8… + 44383.9…

63300 (m²) (63326.8… (m²)) (A1)(ft)(G3)

Note: Follow through from parts (a) and (b)(ii).

${\text{DC}} = \frac{{287 \times {\text{sin}}\,\left( {53.0521 \ldots } \right)}}{{{\text{sin}}\,\left( {46.9478 \ldots } \right)}} = 313.884 \ldots$

$0.5 \times 287 \times 185 \times {\text{sin}}\,85^\circ + 0.5 \times 250 \times 313.884 \ldots \times {\text{sin}}\,70^\circ$ M1M1M1

Note: Award (M1) for substitution in the area formula for either triangle; (M1) for correct substitution for both areas; (M1) for adding their two areas;

26446.4… + 36869.3…

63300 (63315.8…) (m²) (A1)(ft)(G3)

[4 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

Farmer Brown has built a new barn, on horizontal ground, on his farm. The barn has a cuboid base and a triangular prism roof, as shown in the diagram.

The cuboid has a width of 10 m, a length of 16 m and a height of 5 m.
The roof has two sloping faces and two vertical and identical sides, ADE and GLF.
The face DEFL slopes at an angle of 15° to the horizontal and ED = 7 m .

The roof was built using metal supports. Each support is made from five lengths of metal AE, ED, AD, EM and MN, and the design is shown in the following diagram.

ED = 7 m , AD = 10 m and angle ADE = 15° .
M is the midpoint of AD.
N is the point on ED such that MN is at right angles to ED.

Farmer Brown believes that N is the midpoint of ED.

Calculate the area of triangle EAD.

[3]

Calculate the total volume of the barn.

[3]

Calculate the length of MN.

[2]

Calculate the length of AE.

[3]

Show that Farmer Brown is incorrect.

[3]

Calculate the total length of metal required for one support.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(Area of EAD =) $\frac{1}{2} \times 10 \times 7 \times {\text{sin}}15$ (M1)(A1)

Note: Award (M1) for substitution into area of a triangle formula, (A1) for correct substitution. Award (M0)(A0)(A0) if EAD or AED is considered to be a right-angled triangle.

= 9.06 m² (9.05866… m²) (A1) (G3)

[3 marks]

(10 × 5 × 16) + (9.05866… × 16) (M1)(M1)

Note: Award (M1) for correct substitution into volume of a cuboid, (M1) for adding the correctly substituted volume of their triangular prism.

= 945 m³ (944.938… m³) (A1)(ft) (G3)

Note: Follow through from part (a).

[3 marks]

$\frac{{{\text{MN}}}}{5} = \,\,\,{\text{sin}}15$ (M1)

Note: Award (M1) for correct substitution into trigonometric equation.

(MN =) 1.29(m) (1.29409… (m)) (A1) (G2)

[2 marks]

(AE² =) 10² + 7² − 2 × 10 × 7 × cos 15 (M1)(A1)

Note: Award (M1) for substitution into cosine rule formula, and (A1) for correct substitution.

(AE =) 3.71(m) (3.71084… (m)) (A1) (G2)

[3 marks]

ND² = 5² − (1.29409…)² (M1)

Note: Award (M1) for correct substitution into Pythagoras theorem.

(ND =) 4.83 (4.82962…) (A1)(ft)

Note: Follow through from part (c).

$\frac{{1.29409 \ldots }}{{{\text{ND}}}} = {\text{tan}}\,15^\circ$ (M1)

Note: Award (M1) for correct substitution into tangent.

(ND =) 4.83 (4.82962…) (A1)(ft)

Note: Follow through from part (c).

$\frac{{{\text{ND}}}}{5} = {\text{cos }}15^\circ$ (M1)

Note: Award (M1) for correct substitution into cosine.

(ND =) 4.83 (4.82962…) (A1)(ft)

Note: Follow through from part (c).

ND² = 1.29409…² + 5² − 2 × 1.29409… × 5 × cos 75° (M1)

Note: Award (M1) for correct substitution into cosine rule.

(ND =) 4.83 (4.82962…) (A1)(ft)

Note: Follow through from part (c).

4.82962… ≠ 3.5 (ND ≠ 3.5) (R1)(ft)

4.82962… ≠ 2.17038… (ND ≠ NE) (R1)(ft)

(hence Farmer Brown is incorrect)

Note: Do not award (M0)(A0)(R1)(ft). Award (M0)(A0)(R0) for a correct conclusion without any working seen.

[3 marks]

(EM² =) 1.29409…² + (7 − 4.82962…)² (M1)

Note: Award (M1) for their correct substitution into Pythagoras theorem.

(EM² =) 5² + 7² − 2 × 5 × 7 × cos 15 (M1)

Note: Award (M1) for correct substitution into cosine rule formula.

(EM =) 2.53(m) (2.52689...(m)) (A1)(ft) (G2)(ft)

Note: Follow through from parts (c), (d) and (e).

(Total length =) 2.52689… + 3.71084… + 1.29409… +10 + 7 (M1)

Note: Award (M1) for adding their EM, their parts (c) and (d), and 10 and 7.

= 24.5 (m) (24.5318… (m)) (A1)(ft) (G4)

Note: Follow through from parts (c) and (d).

[4 marks]

Examiners report

[N/A]

The following diagram shows a semicircle with centre $O$ and radius $r$ . Points $P, Q$ and $R$ lie on the circumference of the circle, such that $PQ = 2 r$ and $R \hat{O} Q = θ$ , where $0 < θ < π$ .

Given that the areas of the two shaded regions are equal, show that $θ = 2 \sin θ$ .

[5]

Hence determine the value of $θ$ .

[1]

Markscheme

attempt to find the area of either shaded region in terms of $r$ and $θ$ (M1)

Note: Do not award M1 if they have only copied from the booklet and not applied to the shaded area.

Area of segment $= \frac{1}{2} r^{2} θ - \frac{1}{2} r^{2} \sin θ$ A1

Area of triangle $= \frac{1}{2} r^{2} \sin (π - θ)$ A1

correct equation in terms of $θ$ only (A1)

$θ - \sin θ = \sin (π - θ)$

$θ - \sin θ = \sin θ$ A1

$θ = 2 \sin θ$ AG

Note: Award a maximum of M1A1A0A0A0 if a candidate uses degrees (i.e., $\frac{1}{2} r^{2} \sin (180 ° - θ)$ ), even if later work is correct.

Note: If a candidate directly states that the area of the triangle is $\frac{1}{2} r^{2} \sin θ$ , award a maximum of M1A1A0A1A1.

[5 marks]

$θ = 1.89549 \dots$

$θ = 1.90$ A1

Note: Award A0 if there is more than one solution. Award A0 for an answer in degrees.

[1 mark]

Examiners report

[N/A]

A farmer owns a plot of land in the shape of a quadrilateral ABCD.

${\text{AB}} = 105{\text{ m, BC}} = 95{\text{ m, CD}} = 40{\text{ m, DA}} = 70{\text{ m}}$ and angle ${\text{DCB}} = 90^\circ$ .

N16/5/MATSD/SP2/ENG/TZ0/05

The farmer wants to divide the land into two equal areas. He builds a fence in a straight line from point B to point P on AD, so that the area of PAB is equal to the area of PBCD.

Calculate

the length of BD;

[2]

the size of angle DAB;

[3]

the area of triangle ABD;

[3]

the area of quadrilateral ABCD;

[2]

the length of AP;

[3]

the length of the fence, BP.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$({\text{BD}} = ){\text{ }}\sqrt {{{95}^2} + {{40}^2}}$ (M1)

Note: Award (M1) for correct substitution into Pythagoras’ theorem.

$= 103{\text{ }}({\text{m}}){\text{ }}\left( {103.077 \ldots ,{\text{ }}25\sqrt {17} } \right)$ (A1)(G2)

[2 marks]

$\cos {\rm{B\hat AD}} = \frac{{{{105}^2} + {{70}^2} - {{(103.077 \ldots )}^2}}}{{2 \times 105 \times 70}}$ (M1)(A1)(ft)

Note: Award (M1) for substitution into cosine rule, (A1)(ft) for their correct substitutions. Follow through from part (a).

$({\rm{B\hat AD}}) = 68.9^\circ {\text{ }}(68.8663 \ldots )$ (A1)(ft)(G2)

Note: If their 103 used, the answer is $68.7995 \ldots$

[3 marks]

$({\text{Area of ABD}} = )\frac{1}{2} \times 105 \times 70 \times \sin (68.8663 \ldots )$ (M1)(A1)(ft)

Notes: Award (M1) for substitution into the trig form of the area of a triangle formula.

Award (A1)(ft) for their correct substitutions.

Follow through from part (b).

If 68.8° is used the area $= 3426.28 \ldots {\text{ }}{{\text{m}}^2}$ .

$= 3430{\text{ }}{{\text{m}}^2}{\text{ }}(3427.82 \ldots )$ (A1)(ft)(G2)

[3 marks]

${\text{area of ABCD}} = \frac{1}{2} \times 40 \times 95 + 3427.82 \ldots$ (M1)

Note: Award (M1) for correctly substituted area of triangle formula added to their answer to part (c).

$= 5330{\text{ }}{{\text{m}}^2}{\text{ }}(5327.83 \ldots )$ (A1)(ft)(G2)

[2 marks]

$\frac{1}{2} \times 105 \times {\text{AP}} \times \sin (68.8663 \ldots ) = 0.5 \times 5327.82 \ldots$ (M1)(M1)

Notes: Award (M1) for the correct substitution into triangle formula.

Award (M1) for equating their triangle area to half their part (d).

$({\text{AP}} = ){\text{ }}54.4{\text{ }}({\text{m}}){\text{ }}(54.4000 \ldots )$ (A1)(ft)(G2)

Notes: Follow through from parts (b) and (d).

[3 marks]

${\text{B}}{{\text{P}}^2} = {105^2} + {(54.4000 \ldots )^2} - 2 \times 105 \times (54.4000 \ldots ) \times \cos (68.8663 \ldots )$ (M1)(A1)(ft)

Notes: Award (M1) for substituted cosine rule formula.

Award (A1)(ft) for their correct substitutions. Accept the exact fraction $\frac{{53}}{{147}}$ in place of $\cos (68.8663 \ldots )$ .

Follow through from parts (b) and (e).

$({\text{BP}} = ){\text{ }}99.3{\text{ }}({\text{m}}){\text{ }}(99.3252 \ldots )$ (A1)(ft)(G2)

Notes: If 54.4 and $\cos (68.9)$ are used the answer is $99.3567 \ldots$

[3 marks]

Examiners report

[N/A]

The base of an electric iron can be modelled as a pentagon ABCDE, where:

$\begin{array}{*{20}{l}} {{\text{BCDE is a rectangle with sides of length }}(x + 3){\text{ cm and }}(x + 5){\text{ cm;}}} \\ {{\text{ABE is an isosceles triangle, with AB}} = {\text{AE and a height of }}x{\text{ cm;}}} \\ {{\text{the area of ABCDE is 222 c}}{{\text{m}}^{\text{2}}}{\text{.}}} \end{array}$

M17/5/MATSD/SP2/ENG/TZ1/02

Insulation tape is wrapped around the perimeter of the base of the iron, ABCDE.

F is the point on AB such that ${\text{BF}} = {\text{8 cm}}$ . A heating element in the iron runs in a straight line, from C to F.

Write down an equation for the area of ABCDE using the above information.

[2]

a.i.

Show that the equation in part (a)(i) simplifies to $3{x^2} + 19x - 414 = 0$ .

[2]

a.ii.

Find the length of CD.

[2]

Show that angle ${\rm{B\hat AE}} = 67.4^\circ$ , correct to one decimal place.

[3]

Find the length of the perimeter of ABCDE.

[3]

Calculate the length of CF.

[4]

Markscheme

$222 = \frac{1}{2}x(x + 3) + (x + 3)(x + 5)$ (M1)(M1)(A1)

Note: Award (M1) for correct area of triangle, (M1) for correct area of rectangle, (A1) for equating the sum to 222.

$222 = (x + 3)(2x + 5) - 2\left( {\frac{1}{4}} \right)x(x + 3)$ (M1)(M1)(A1)

Note: Award (M1) for area of bounding rectangle, (M1) for area of triangle, (A1) for equating the difference to 222.

[2 marks]

a.i.

$222 = \frac{1}{2}{x^2} + \frac{3}{2}x + {x^2} + 3x + 5x + 15$ (M1)

Note: Award (M1) for complete expansion of the brackets, leading to the final answer, with no incorrect working seen. The final answer must be seen to award (M1).

$3{x^2} + 19x - 414 = 0$ (AG)

[2 marks]

a.ii.

$x = 9{\text{ }}\left( {{\text{and }}x = - \frac{{46}}{3}} \right)$ (A1)

${\text{CD}} = 12{\text{ (cm)}}$ (A1)(G2)

[2 marks]

$\frac{1}{2}({\text{their }}x + 3) = 6$ (A1)(ft)

Note: Follow through from part (b).

$\tan \left( {\frac{{{\rm{B\hat AE}}}}{2}} \right) = \frac{6}{9}$ (M1)

Note: Award (M1) for their correct substitutions in tangent ratio.

${\rm{B\hat AE}} = 67.3801 \ldots ^\circ$ (A1)

$= 67.4^\circ$ (AG)

Note: Do not award the final (A1) unless both the correct unrounded and rounded answers are seen.

$\frac{1}{2}({\text{their }}x + 3) = 6$ (A1)(ft)

$\tan ({\rm{A\hat BE}}) = \frac{9}{6}$ (M1)

Note: Award (M1) for their correct substitutions in tangent ratio.

${\rm{B\hat AE}} = 180^\circ - 2({\rm{A\hat BE}})$

${\rm{B\hat AE}} = 67.3801 \ldots ^\circ$ (A1)

$= 67.4^\circ$ (AG)

Note: Do not award the final (A1) unless both the correct unrounded and rounded answers are seen.

[3 marks]

$2\sqrt {{9^2} + {6^2}} + 12 + 2(14)$ (M1)(M1)

Note: Award (M1) for correct substitution into Pythagoras. Award (M1) for the addition of 5 sides of the pentagon, consistent with their $x$ .

$61.6{\text{ (cm) }}\left( {61.6333 \ldots {\text{ (cm)}}} \right)$ (A1)(ft)(G3)

Note: Follow through from part (b).

[3 marks]

${\rm{F\hat BC}} = 90 + \left( {\frac{{180 - 67.4}}{2}} \right){\text{ }}( = 146.3^\circ )$ (M1)

$180 - \frac{{67.4}}{2}$ (M1)

${\rm{C}}{{\text{F}}^2} = {8^2} + {14^2} - 2(8)(14)\cos (146.3^\circ )$ (M1)(A1)(ft)

Note: Award (M1) for substituted cosine rule formula and (A1) for correct substitutions. Follow through from part (b).

${\text{CF}} = 21.1{\text{ (cm) }}(21.1271 \ldots )$ (A1)(ft)(G3)

${\rm{G\hat BF}} = \frac{{67.4}}{2} = 33.7^\circ$ (A1)

Note: Award (A1) for angle ${\rm{G\hat BF}} = 33.7^\circ$ , where G is the point such that CG is a projection/extension of CB and triangles BGF and CGF are right-angled triangles. The candidate may use another variable.

M17/5/MATSD/SP2/ENG/TZ1/02.e/M

${\text{GF}} = 8\sin 33.7^\circ = 4.4387 \ldots$ $\,\,\,$ AND $\,\,\,$ ${\text{BG}} = 8\cos 33.7^\circ = 6.6556 \ldots$ (M1)

Note: Award (M1) for correct substitution into trig formulas to find both GF and BG.

${\text{C}}{{\text{F}}^2} = {(14 + 6.6556 \ldots )^2} + {(4.4387 \ldots )^2}$ (M1)

Note: Award (M1) for correct substitution into Pythagoras formula to find CF.

${\text{CF}} = 21.1{\text{ (cm) }}(21.1271 \ldots )$ (A1)(ft)(G3)

[4 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

The following diagram shows a circle with centre $O$ and radius $3$ .

Points $A$ , $P$ and $B$ lie on the circumference of the circle.

Chord $[AB]$ has length $L$ and $A \hat{O} B = θ$ radians.

Show that arc $APB$ has length $6 π - 3 θ$ .

[2]

Show that $L = \sqrt{18 - 18 \cos θ}$ .

[2]

Arc $APB$ is twice the length of chord $[AB]$ .

Find the value of $θ$ .

[3]

Markscheme

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

EITHER

uses the arc length formula (M1)

arc length is $3 (2 π - θ)$ A1

length of arc $AB$ is $3 θ$ A1

the sum of the lengths of arc $AB$ and arc $APB$ is $6 π$ A1

THEN

so arc $APB$ has length $6 π - 3 θ$ AG

[2 marks]

uses the cosine rule (M1)

$L^{2} = 3^{2} + 3^{2} - 2 (3) (3) \cos θ$ A1

so $L = \sqrt{18 - 18 \cos θ}$ AG

[2 marks]

$6 π - 3 θ = 2 \sqrt{18 - 18 \cos θ}$ A1

attempts to solve for $θ$ (M1)

$θ = 2.49$ A1

[3 marks]

Examiners report

[N/A]

All lengths in this question are in centimetres.

A solid metal ornament is in the shape of a right pyramid, with vertex $V$ and square base $ABCD$ . The centre of the base is $X$ . Point $V$ has coordinates $(1, 5, 0)$ and point $A$ has coordinates $(- 1, 1, 6)$ .

The volume of the pyramid is $57.2 {cm}^{3}$ , correct to three significant figures.

Find $AV$ .

[2]

Given that $A \hat{V} B = 40 °$ , find $AB$ .

[3]

Find the height of the pyramid, $VX$ .

[3]

A second ornament is in the shape of a cuboid with a rectangular base of length $2 x cm$ , width $x cm$ and height $y cm$ . The cuboid has the same volume as the pyramid.

The cuboid has a minimum surface area of $S {cm}^{2}$ . Find the value of $S$ .

[5]

Markscheme

attempt to use the distance formula to find $AV$ (M1)

$\sqrt{{(1 - (- 1))}^{2} + {(5 - 1)}^{2} + {(0 - 6)}^{2}}$

$= 7.48331 \dots$

$= 7.48 (cm) (= \sqrt{56} or 2 \sqrt{14})$ A1

[2 marks]

METHOD 1

attempt to apply cosine rule OR sine rule to find $AB$ (M1)

$(AB =) \sqrt{7.48 \dots^{2} + 7.48 \dots^{2} - 2 \times 7.48 \dots \times 7.48 \dots \cos (40 °)}$ OR $\frac{AB}{\sin 40 °} = \frac{\sqrt{56}}{\sin 70 °}$ (A1)

$= 5.11888 \dots$

$= 5.12 (cm)$ A1

METHOD 2

Let $M$ be the midpoint of $[AB]$

attempt to apply right-angled trigonometry on triangle $AVM$ (M1)

$= 2 \times 7.48 \dots \times \sin (20 °)$ (A1)

$= 5.11888 \dots$

$= 5.12 (cm)$ A1

[3 marks]

METHOD 1

equating volume of pyramid formula to $57.2$ (M1)

$\frac{1}{3} \times 5.11 \dots^{2} \times h = 57.2$ (A1)

$h = 6.54886 \dots$

$h = 6.55 (cm)$ A1

METHOD 2

Let $M$ be the midpoint of $[AB]$

${AV}^{2} = {AM}^{2} + {MX}^{2} + {XV}^{2}$ (M1)

$\Rightarrow XV = \sqrt{7.48 \dots^{2} - {(\frac{5.11 \dots}{2})}^{2} - {(\frac{5.11 \dots}{2})}^{2}}$ (A1)

$h = 6.54886 \dots$

$h = 6.55 (cm)$ A1

[3 marks]

$V = x \times 2 x \times y = 57.2$ (A1)

$S = 2 (2 x^{2} + x y + 2 x y)$ A1

Note: Condone use of $A$ .

attempt to substitute $y = \frac{57.2}{2 x^{2}}$ into their expression for surface area (M1)

$(S (x) =) 4 x^{2} + 6 x (\frac{57.2}{2 x^{2}})$

EITHER

attempt to find minimum turning point on graph of area function (M1)

$\frac{d S}{d x} = 8 x - 171.6 x^{- 2} = 0$ OR $x = 2.77849 \dots$ (M1)

THEN

$92.6401 \dots$

minimum surface area $= 92.6 ({cm}^{2})$ A1

[5 marks]

Examiners report

Parts (a), (b) and (c) were completed well by many candidates, but few were able to make any significant progress in part (d).

In part (a), many candidates were able to apply the distance formula and successfully find AV. However, a common error was to work in two-dimensions and to apply Pythagoras' Theorem once, neglecting completely the z-coordinates. Many recognised the need to use either the sine or cosine rule in part (b) to find the length AB. Common errors in this part included: the GDC being set incorrectly in radians; applying right-angled trigonometry on a 40°, 40°, 70° triangle; or using $\frac{1}{2} AB$ as the length of AX in triangle AVX.

Despite the formula for the volume of a pyramid being in the formula booklet, a common error in part (c) was to omit the factor of $\frac{1}{3}$ from the volume formula, or not to recognise that the area of the base of the pyramid was ${AB}^{2}$ .

The most challenging part of this question proved to be the optimization of the surface area of the cuboid in part (d). Although some candidates were able to form an equation involving the volume of the cuboid, an expression for the surface area eluded most. A common error was to gain a surface area which involved eight sides rather than six. It was surprising that few who were able to find both the equation and an expression were able to progress any further. Of those that did, few used their GDC to find the minimum surface area directly, with most preferring the more time consuming analytical approach.

[N/A]

A scientist conducted a nine-week experiment on two plants, $A$ and $B$ , of the same species. He wanted to determine the effect of using a new plant fertilizer. Plant $A$ was given fertilizer regularly, while Plant $B$ was not.

The scientist found that the height of Plant $A, h_{A} cm$ , at time $t$ weeks can be modelled by the function $h_{A} (t) = \sin (2 t + 6) + 9 t + 27$ , where $0 \leq t \leq 9$ .

The scientist found that the height of Plant $B, h_{B} cm$ , at time $t$ weeks can be modelled by the function $h_{B} (t) = 8 t + 32$ , where $0 \leq t \leq 9$ .

Use the scientist’s models to find the initial height of

Plant $B$ .

[1]

a.i.

Plant $A$ correct to three significant figures.

[2]

a.ii.

Find the values of $t$ when $h_{A} (t) = h_{B} (t)$ .

[3]

For $0 \leq t \leq 9$ , find the total amount of time when the rate of growth of Plant $B$ was greater than the rate of growth of Plant $A$ .

[6]

Markscheme

$32$ (cm) A1

[1 mark]

a.i.

$h_{A} (0) = \sin (6) + 27$ (M1)

$= 26.7205 \dots$

$= 26.7$ (cm) A1

[2 marks]

a.ii.

attempts to solve $h_{A} (t) = h_{B} (t)$ for $t$ (M1)

$t = 4.00746 \dots, 4.70343 \dots, 5.88332 \dots$

$t = 4.01, 4.70, 5.88$ (weeks) A2

[3 marks]

recognises that $h_{A}' (t)$ and $h_{B}' (t)$ are required (M1)

attempts to solve $h_{A}' (t) = h_{B}' (t)$ for $t$ (M1)

$t = 1.18879 \dots$ and $2.23598 \dots$ OR $4.33038 \dots$ and $5.37758 \dots$ OR $7.47197 \dots$ and $8.51917 \dots$ (A1)

Note: Award full marks for $t = \frac{4 π}{3} - 3, \frac{5 π}{3} - 3, (\frac{7 π}{3} - 3, \frac{8 π}{3} - 3 \frac{10 π}{3} - 3, \frac{11 π}{3} - 3)$ .

Award subsequent marks for correct use of these exact values.

$1.18879 \dots < t < 2.23598 \dots$ OR $4.33038 \dots < t < 5.37758 \dots$ OR

$7.47197 \dots < t < 8.51917 \dots$ (A1)

attempts to calculate the total amount of time (M1)

$3 (2.2359 \dots - 1.1887 \dots) (= 3 ((\frac{5 π}{3} - 3) - (\frac{4 π}{3} - 3)))$

$= 3.14 (= π)$ (weeks) A1

[6 marks]

Examiners report

Many students did not change their calculators back to radian mode. This meant they had no chance of correctly answering parts (c) and (d), since even if follow through was given, there were not enough intersections on the graphs.

Most managed part (a) and some attempted to equate the functions in part b) but few recognised that 'rate of growth' was the derivatives of the given functions, and of those who did, most were unable to find them.

Almost all the candidates who did solve part (c) gave the answer $3 \times 1.05 = 3.15$ , when working with more significant figures would have given them 3.14. They lost the last mark.

a.i.

[N/A]

a.ii.

[N/A]

At Grande Anse Beach the height of the water in metres is modelled by the function $h(t) = p\cos (q \times t) + r$ , where $t$ is the number of hours after 21:00 hours on 10 December 2017. The following diagram shows the graph of $h$ , for $0 \leqslant t \leqslant 72$ .

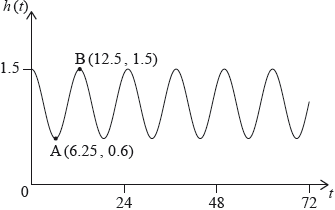
M17/5/MATME/SP2/ENG/TZ1/08

The point ${\text{A}}(6.25,{\text{ }}0.6)$ represents the first low tide and ${\text{B}}(12.5,{\text{ }}1.5)$ represents the next high tide.

How much time is there between the first low tide and the next high tide?

[2]

a.i.

Find the difference in height between low tide and high tide.

[2]

a.ii.

Find the value of $p$ ;

[2]

b.i.

Find the value of $q$ ;

[3]

b.ii.

Find the value of $r$ .

[2]

b.iii.

There are two high tides on 12 December 2017. At what time does the second high tide occur?

[3]

Markscheme

attempt to find the difference of $x$ -values of A and B (M1)

eg $\,\,\,\,\,$ $6.25 - 12.5{\text{ }}$

6.25 (hours), (6 hours 15 minutes) A1 N2

[2 marks]

a.i.

attempt to find the difference of $y$ -values of A and B (M1)

eg $\,\,\,\,\,$ $1.5 - 0.6$

$0.9{\text{ (m)}}$ A1 N2

[2 marks]

a.ii.

valid approach (M1)

eg $\,\,\,\,\,$ $\frac{{{\text{max}} - {\text{min}}}}{2},{\text{ }}0.9 \div 2$

$p = 0.45$ A1 N2

[2 marks]

b.i.

METHOD 1

period $= 12.5$ (seen anywhere) (A1)

valid approach (seen anywhere) (M1)

eg $\,\,\,\,\,$ ${\text{period}} = \frac{{2\pi }}{b},{\text{ }}q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{12.5}}$

0.502654

$q = \frac{{4\pi }}{{25}},{\text{ 0.503 }}\left( {{\text{or }} - \frac{{4\pi }}{{25}},{\text{ }} - 0.503} \right)$ A1 N2

METHOD 2

attempt to use a coordinate to make an equation (M1)

eg $\,\,\,\,\,$ $p\cos (6.25q) + r = 0.6,{\text{ }}p\cos (12.5q) + r = 1.5$

correct substitution (A1)

eg $\,\,\,\,\,$ $0.45\cos (6.25q) + 1.05 = 0.6,{\text{ }}0.45\cos (12.5q) + 1.05 = 1.5$

0.502654

$q = \frac{{4\pi }}{{25}},{\text{ }}0.503{\text{ }}\left( {{\text{or }} - \frac{{4\pi }}{{25}},{\text{ }} - 0.503} \right)$ A1 N2

[3 marks]

b.ii.

valid method to find $r$ (M1)

eg $\,\,\,\,\,$ $\frac{{{\text{max}} + {\text{min}}}}{2},{\text{ }}0.6 + 0.45$

$r = 1.05$ A1 N2

[2 marks]

b.iii.

METHOD 1

attempt to find start or end $t$ -values for 12 December (M1)

eg $\,\,\,\,\,$ $3 + 24,{\text{ }}t = 27,{\text{ }}t = 51$

finds $t$ -value for second max (A1)

$t = 50$

23:00 (or 11 pm) A1 N3

METHOD 2

valid approach to list either the times of high tides after 21:00 or the $t$ -values of high tides after 21:00, showing at least two times (M1)

eg $\,\,\,\,\,$ ${\text{21:00}} + 12.5,{\text{ 21:00}} + 25,{\text{ }}12.5 + 12.5,{\text{ }}25 + 12.5$

correct time of first high tide on 12 December (A1)

eg $\,\,\,\,\,$ 10:30 (or 10:30 am)

time of second high tide = 23:00 A1 N3

METHOD 3

attempt to set their $h$ equal to 1.5 (M1)

eg $\,\,\,\,\,$ $h(t) = 1.5,{\text{ }}0.45\cos \left( {\frac{{4\pi }}{{25}}t} \right) + 1.05 = 1.5$

correct working to find second max (A1)

eg $\,\,\,\,\,$ $0.503t = 8\pi ,{\text{ }}t = 50$

23:00 (or 11 pm) A1 N3

[3 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

b.iii.

[N/A]

A factory packages coconut water in cone-shaped containers with a base radius of 5.2 cm and a height of 13 cm.

The factory designers are currently investigating whether a cone-shaped container can be replaced with a cylinder-shaped container with the same radius and the same total surface area.

Find the volume of one cone-shaped container.

[2]

Find the slant height of the cone-shaped container.

[2]

Show that the total surface area of the cone-shaped container is 314 cm², correct to three significant figures.

[3]

Find the height, $h$ , of this cylinder-shaped container.

[4]

The factory director wants to increase the volume of coconut water sold per container.

State whether or not they should replace the cone-shaped containers with cylinder‑shaped containers. Justify your conclusion.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{{\pi {{\left( {5.2} \right)}^2} \times 13}}{3}$ (M1)

Note: Award (M1) for correct substitution in the volume formula for cone.

368 (368.110…) cm³ (A1)(G2)

Note: Accept 117.173… $\pi$ cm³ or $\frac{{8788}}{{75}}\pi$ cm³.

[2 marks]

(slant height²) = (5.2)² + 13² (M1)

Note: Award (M1) for correct substitution into the formula.

14.0 (14.0014…) (cm) (A1)(G2)

[2 marks]

14.0014… × (5.2) × $\pi$ + (5.2)² × $\pi$ (M1)(M1)

Note: Award (M1) for their correct substitution in the curved surface area formula for cone; (M1) for adding the correct area of the base. The addition must be explicitly seen for the second (M1) to be awarded. Do not accept rounded values here as may come from working backwards.

313.679… (cm²) (A1)

Note: Use of 3 sf value 14.0 gives an unrounded answer of 313.656….

314 (cm²) (AG)

Note: Both the unrounded and rounded answers must be seen for the final (A1) to be awarded.

[3 marks]

2 × $\pi$ × (5.2) × $h$ + 2 × $\pi$ × (5.2)² = 314 (M1)(M1)(M1)

Note: Award (M1) for correct substitution in the curved surface area formula for cylinder; (M1) for adding two correct base areas of the cylinder; (M1) for equating their total cylinder surface area to 314 (313.679…). For this mark to be awarded the areas of the two bases must be added to the cylinder curved surface area and equated to 314. Award at most (M1)(M0)(M0) for cylinder curved surface area equated to 314.

( $h$ =) 4.41 (4.41051…) (cm) (A1)(G3)

[4 marks]

$\pi$ × (5.2)² × 4.41051… (M1)

Note: Award (M1) for correct substitution in the volume formula for cylinder.

375 (374.666…) (cm³) (A1)(ft)(G2)

Note: Follow through from part (d).

375 (cm³) > 368 (cm³) (R1)(ft)

“volume of cylinder is larger than volume of cone” or similar (R1)(ft)

Note: Follow through from their answer to part (a). The verbal statement should be consistent with their answers from parts (e) and (a) for the (R1) to be awarded.

replace with the cylinder containers (A1)(ft)

Note: Do not award (A1)(ft)(R0). Follow through from their incorrect volume for the cylinder in this question part but only if substitution in the volume formula shown.

[4 marks]

Examiners report

[N/A]

A communication tower, T, produces a signal that can reach cellular phones within a radius of 32 km. A straight road passes through the area covered by the tower’s signal.

The following diagram shows a line representing the road and a circle representing the area covered by the tower’s signal. Point R is on the circumference of the circle and points S and R are on the road. Point S is 38 km from the tower and RŜT = 43˚.

Let SR = $x$ . Use the cosine rule to show that ${x^2} - \left( {76\,{\text{cos}}\,43^\circ } \right)x + 420 = 0$ .

[2]

Hence or otherwise, find the total distance along the road where the signal from the tower can reach cellular phones.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

recognizing TR =32 (seen anywhere, including diagram) A1

correct working A1

eg ${32^2} = {x^2} + {38^2} - 2\left( x \right)\left( {38} \right){\text{cos}}\,43^\circ$ , $1024 = 1444 + {x^2} - 76\,\left( x \right){\text{cos}}\,43^\circ$

${x^2} - \left( {76\,{\text{cos}}\,43^\circ } \right)x + 420 = 0$ AG N0

[2 marks]

Note: There are many approaches to this question, depending on which triangle the candidate has used, and whether they used the cosine rule and/or the sine rule. Please check working carefully and award marks in line with the markscheme.

METHOD 1

correct values for $x$ (seen anywhere) A1A1

$x$ = 9.02007, 46.5628

recognizing the need to find difference in values of $x$ (M1)

eg 46.5 − 9.02, ${x_1} - {x_2}$

37.5427

37.5 (km) A1 N2

METHOD 2

correct use of sine rule in ΔSRT

eg $\frac{{{\text{sin}}\,{\text{S}}\mathop {\text{R}}\limits^ \wedge {\text{T}}}}{{38}} = \frac{{{\text{sin}}\,43^\circ }}{{32}}$ , ${{\text{S}}\mathop {\text{R}}\limits^ \wedge {\text{T}}}$ = 54.0835° (A1)

recognizing isosceles triangle (seen anywhere) (M1)

eg $\hat T = 180^\circ - 2 \cdot 54.0835^\circ$ , two sides of 32

correct working to find distance A1

eg $\sqrt {{{32}^2} + {{32}^2} - 2 \cdot 32 \cdot 32\,{\text{cos}}\,\left( {180^\circ - \,2 \cdot 54.0835^\circ } \right)}$ ,

$\frac{{{\text{sin}}\,71.8329^\circ }}{d} = \frac{{{\text{sin}}\,54.0835^\circ }}{{32}}$ , ${32^2} = {32^2} + {x^2} - 2 \cdot 32x\,{\text{cos}}\left( {{\text{0}}{\text{.944}}} \right)$

37.5427

37.5 (km) A1 N2

[4 marks]

Examiners report

[N/A]

The following diagram shows a circle with centre $O$ and radius $5$ metres.

Points $A$ and $B$ lie on the circle and $A \hat{O} B = 1.9$ radians.

Find the length of the chord $[AB]$ .

[3]

Find the area of the shaded sector.

[3]

Markscheme

EITHER

uses the cosine rule (M1)

${AB}^{2} = 5^{2} + 5^{2} - 2 \times 5 \times 5 \times \cos 1.9$ (A1)

uses right-angled trigonometry (M1)

$\frac{\frac{AB}{2}}{5} \sin 0.95$ (A1)

uses the sine rule (M1)

$α = \frac{1}{2} (π - 1.9) (= 0.6207 \dots)$

$\frac{AB}{\sin 1.9} = \frac{5}{\sin 0.6207 \dots}$ (A1)

THEN

$AB = 8.13415 \dots$

$AB = 8.13 (m)$ A1

[3 marks]

let the shaded area be $A$

METHOD 1

attempt at finding reflex angle (M1)

$A \hat{O} B = 2 π - 1.9 (= 4.3831 \dots)$

substitution into area formula (A1)

$A = \frac{1}{2} \times 5^{2} \times 4.3831 \dots$ OR $(\frac{2 π - 1.9}{2 π}) \times π (5^{2})$

$= 54.7898 \dots$

$= 54.8 (m^{2})$ A1

METHOD 2

let the area of the circle be $A_{C}$ and the area of the unshaded sector be $A_{U}$

$A = A_{C} - A_{U}$ (M1)

$A = π \times 5^{2} - \frac{1}{2} \times 5^{2} \times 1.9 (= 78.5398 \dots - 23.75)$ (A1)

$= 54.7898 \dots$

$= 54.8 (m^{2})$ A1

[3 marks]

Examiners report

Most students used the cosine rule to correctly find AB in part (a), although many found the arc length instead of the chord.

Part (b) was generally correctly solved. Some candidates found the area of the unshaded region rather than the shaded one.

[N/A]

The diagram below shows a triangular-based pyramid with base ${\text{ADC}}$ .
Edge ${\text{BD}}$ is perpendicular to the edges ${\text{AD}}$ and ${\text{CD}}$ .

${\text{AC}} = 28.4\,{\text{cm}}$ , ${\text{AB}} = x\,{\text{cm}}$ , ${\text{BC}} = x + 2\,{\text{cm}}$ , ${\text{A}}\widehat {\text{B}}{\text{C}} = 0.667$ , ${\text{B}}\widehat {\text{A}}{\text{D}} = 0.611$

Calculate ${\text{AD}}$

Markscheme

evidence of choosing cosine rule (M1)

eg ${a^2} = {b^2} + {c^2} - 2bc\,{\text{cos}}\,A$

correct substitution to find ${\text{AB}}$ (A1)

eg ${28.4^2} = {x^2} + {\left( {x + 2} \right)^2} - 2x\left( {x + 2} \right){\text{cos}}\left( {0.667} \right)$

$x = 42.2822$ A2

appropriate approach to find ${\text{AD}}$ (M1)

eg ${\text{AD}} = x\,{\text{cos}}\left( {0.611} \right)$ , ${\text{cos}}\left( {0.611} \right) = \frac{{{\text{AD}}}}{{42.2822}}$

$34.6322$

${\text{AD}} = 34.6$ A1 N3

[6 marks]

Examiners report

[N/A]

The following diagram shows a triangle ABC.

N17/5/MATME/SP2/ENG/TZ0/01

${\text{AB}} = 5{\rm{ cm, C\hat AB}} =$ 50° and ${\rm{A\hat CB}} =$ 112°

Find BC.

[3]

Find the area of triangle ABC.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of choosing sine rule (M1)

eg $\,\,\,\,\,$ $\frac{{\sin A}}{a} = \frac{{\sin B}}{b}$

correct substitution (A1)

eg $\,\,\,\,\,$ $\frac{{{\text{BC}}}}{{\sin 50}} = \frac{5}{{\sin 112}}$

4.13102

${\text{BC}} = 4.13{\text{ (cm)}}$ A1 N2

[3 marks]

correct working (A1)

eg $\,\,\,\,\,$ ${\rm{\hat B}} = 180 - 50 - 112$ , 18°, ${\text{AC}} = 1.66642$

correct substitution into area formula (A1)

eg $\,\,\,\,\,$ $\frac{1}{2} \times 5 \times 4.13 \times \sin 18,{\text{ }}0.5(5)(1.66642)\sin 50,{\text{ }}\frac{1}{2}(4.13)(1.66642)\sin 112$

3.19139

${\text{area}} = 3.19{\text{ (c}}{{\text{m}}^2}{\text{)}}$ A1 N2

[3 marks]

Examiners report

[N/A]

A flat horizontal area, ABC, is such that AB = 100 m , BC = 50 m and angle AĈB = 43.7° as shown in the diagram.

Show that the size of angle BÂC is 20.2°, correct to 3 significant figures.

[3]

Calculate the area of triangle ABC.

[4]

Find the length of AC.

[3]

A vertical pole, TB, is constructed at point B and has height 25 m.

Calculate the angle of elevation of T from, M, the midpoint of the side AC.

[5]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{{{\text{sin}}\,43.7^\circ }}{{100}} = \frac{{{\text{sin}}\,{\text{BAC}}}}{{50}}$ (M1)(A1)

Note: Award (M1) for substitution into sine rule formula, (A1) for correct substitution.

BAC = 20.2087… = 20.2° (A1)(AG)

Note: Award (A1) only if both the correct unrounded and rounded answers are seen.

[3 marks]

units are required in part (b)

$\frac{1}{2}\left( {100} \right)\left( {50} \right){\text{sin}}\,\left( {116.1} \right)$ (A1)(M1)(A1)

Note: Award (A1) for 116.1 or unrounded value or 116 seen, (M1) for substitution into area of triangle formula, (A1) for correct substitution.

= 2250 m² (2245.06… m²) (A1)(G3)

Note: The answer is 2250 m²; the units are required. Use of 20.2087… gives 2245.23….

[4 marks]

$\frac{{100}}{{{\text{sin}}\,43.7}} = \frac{{{\text{AC}}}}{{{\text{sin}}\,\left( {116.1} \right)}}$ (M1)(A1)(ft)

Note: Award (M1) for substitution into sine rule formula, (A1)(ft) for their correct substitution. Follow through from their 116.1.

AC = 130 (m) (129.982… (m)) (A1)(ft)(G2)

Note: Use of 20.2087… gives 129.992….

AC² = 100² + 50² −2(100)(50) cos (116.1) (M1)(A1)(ft)

Note: Award (M1) for substitution into cosine rule formula, (A1)(ft) for their correct substitution. Follow through from their 116.1.

AC = 130 (m) (129.997… (m)) (A1)(ft)(G2)

Note: Award (M1) for substitution into cosine rule formula, (A1)(ft) for their correct substitution.

[3 marks]

BM² = 100² + 65² − 2(100)(65) cos (20.2°) (M1)(A1)(ft)

BM² = 50² + 65² − 2(50)(65) cos (43.7°) (M1)(A1)(ft)

Note: Award (M1) for substitution into cosine rule formula, (A1)(ft) for correct substitution, including half their AC.

BM = 45.0 (44.9954… OR 45.0079…) (A1)(ft)

Note: Use of 20.2052… gives 45. Award (G2) for 45.0 seen without working.

${\text{tan}}\,\left( {{\text{TMB}}} \right) = \frac{{25}}{{{\text{their BM}}}}$ (M1)

Note: Award (M1) for correct substitution into tangent formula.

T $\mathop {\text{M}}\limits^ \wedge$ B = 29.1° (29.0546…°) (A1)(ft)(G4)

Note: Follow through within part (d) provided their BM is seen. Use of 44.9954 gives 29.0570… and use of 45.0079… gives 29.0503…. Follow through from their AC in part (c).

[5 marks]

Examiners report

[N/A]

The following diagram shows a circle with centre O and radius 40 cm.

M17/5/MATME/SP2/ENG/TZ2/01

The points A, B and C are on the circumference of the circle and ${\rm{A\hat OC}} = 1.9{\text{ radians}}$ .

Find the length of arc ABC.

[2]

Find the perimeter of sector OABC.

[2]

Find the area of sector OABC.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct substitution into arc length formula (A1)

eg $\,\,\,\,\,$ $(40)(1.9)$

${\text{arc length}} = 76{\text{ (cm)}}$ A1 N2

[2 marks]

valid approach (M1)

eg $\,\,\,\,\,$ ${\text{arc}} + 2r,{\text{ }}76 + 40 + 40$

${\text{perimeter}} = 156{\text{ (cm)}}$ A1 N2

[2 marks]

correct substitution into area formula (A1)

eg $\,\,\,\,\,$ $\frac{1}{2}(1.9){(40)^2}$

${\text{area}} = 1520{\text{ (c}}{{\text{m}}^{\text{2}}}{\text{)}}$ A1 N2

[2 marks]

Examiners report

[N/A]

Let $f\left( x \right) = \frac{{16}}{x}$ . The line $L$ is tangent to the graph of $f$ at $x = 8$ .

$L$ can be expressed in the form r $= \left( {\begin{array}{*{20}{c}} 8 \\ 2 \end{array}} \right) + t$ u.

The direction vector of $y = x$ is $\left( {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right)$ .

Find the gradient of $L$ .

[2]

Find u.

[2]

Find the acute angle between $y = x$ and $L$ .

[5]

Find $\left( {f \circ f} \right)\left( x \right)$ .

[3]

d.i.

Hence, write down ${f^{ - 1}}\left( x \right)$ .

[1]

d.ii.

Hence or otherwise, find the obtuse angle formed by the tangent line to $f$ at $x = 8$ and the tangent line to $f$ at $x = 2$ .

[3]

d.iii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to find $f'\left( 8 \right)$ (M1)

eg $f'\left( x \right)$ , ${y'}$ , $- 16{x^{ - 2}}$

−0.25 (exact) A1 N2

[2 marks]

u null or any scalar multiple A2 N2

[2 marks]

correct scalar product and magnitudes (A1)(A1)(A1)

scalar product $= 1 \times 4 + 1 \times - 1\,\,\,\left( { = 3} \right)$

magnitudes $= \sqrt {{1^2} + {1^2}}$ , $\sqrt {{4^2} + {{\left( { - 1} \right)}^2}}$ $\left( { = \sqrt 2 {\text{,}}\,\,\sqrt {17} } \right)$

substitution of their values into correct formula (M1)

eg $\frac{{4 - 1}}{{\sqrt {{1^2} + {1^2}} \sqrt {{4^2} + {{\left( { - 1} \right)}^2}} }}$ , $\frac{{ - 3}}{{\sqrt 2 \sqrt {17} }}$ , 2.1112, 120.96°

1.03037 , 59.0362°

angle = 1.03 , 59.0° A1 N4

[5 marks]

attempt to form composite $\left( {f \circ f} \right)\left( x \right)$ (M1)

eg $f\left( {f\left( x \right)} \right)$ , $f\left( {\frac{{16}}{x}} \right)$ , $\frac{{16}}{{f\left( x \right)}}$

correct working (A1)

eg $\frac{{16}}{{\frac{{16}}{x}}}$ , $16 \times \frac{x}{{16}}$

$\left( {f \circ f} \right)\left( x \right) = x$ A1 N2

[3 marks]

d.i.

${f^{ - 1}}\left( x \right) = \frac{{16}}{x}$ (accept $y = \frac{{16}}{x}$ , $\frac{{16}}{x}$ ) A1 N1

Note: Award A0 in part (ii) if part (i) is incorrect.
Award A0 in part (ii) if the candidate has found ${f^{ - 1}}\left( x \right) = \frac{{16}}{x}$ by interchanging $x$ and $y$ .

[1 mark]

d.ii.

METHOD 1

recognition of symmetry about $y = x$ (M1)

eg (2, 8) ⇔ (8, 2)

evidence of doubling their angle (M1)

eg $2 \times 1.03$ , $2 \times 59.0$

2.06075, 118.072°

2.06 (radians) (118 degrees) A1 N2

METHOD 2

finding direction vector for tangent line at $x = 2$ (A1)

eg $\left( {\begin{array}{*{20}{c}} { - 1} \\ 4 \end{array}} \right)$ , $\left( {\begin{array}{*{20}{c}} 1 \\ { - 4} \end{array}} \right)$

substitution of their values into correct formula (must be from vectors) (M1)

eg $\frac{{ - 4 - 4}}{{\sqrt {{1^2} + {4^2}} \sqrt {{4^2} + {{\left( { - 1} \right)}^2}} }}$ , $\frac{8}{{\sqrt {17} \sqrt {17} }}$

2.06075, 118.072°

2.06 (radians) (118 degrees) A1 N2

METHOD 3

using trigonometry to find an angle with the horizontal (M1)

eg ${\text{tan}}\,\theta = - \frac{1}{4}$ , ${\text{tan}}\,\theta = - 4$

finding both angles of rotation (A1)

eg ${\theta _1} = 0.244978{\text{, 14}}{\text{.0362}}^\circ$ , ${\theta _1} = 1.81577{\text{, 104}}{\text{.036}}^\circ$

2.06075, 118.072°

2.06 (radians) (118 degrees) A1 N2

[3 marks]

d.iii.

Examiners report

[N/A]

d.i.

[N/A]

d.ii.

[N/A]

d.iii.

The following diagram shows the chord [AB] in a circle of radius 8 cm, where ${\text{AB}} = 12{\text{ cm}}$ .

M17/5/MATME/SP2/ENG/TZ1/05

Find the area of the shaded segment.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to find the central angle or half central angle (M1)

eg $\,\,\,\,\,$ M17/5/MATME/SP2/ENG/TZ1/05/M , cosine rule, right triangle

correct working (A1)

eg $\,\,\,\,\,$ $\cos \theta = \frac{{{8^2} + {8^2} - {{12}^2}}}{{2 \bullet 8 \bullet 8}},{\text{ }}{\sin ^{ - 1}}\left( {\frac{6}{8}} \right),{\text{ }}0.722734,{\text{ }}41.4096^\circ ,{\text{ }}\frac{\pi }{2} - {\sin ^{ - 1}}\left( {\frac{6}{8}} \right)$

correct angle ${\rm{A\hat OB}}$ (seen anywhere)

eg $\,\,\,\,\,$ ${\text{1.69612, }}97.1807^\circ ,{\text{ 2}} \times {\text{si}}{{\text{n}}^{ - 1}}\left( {\frac{6}{8}} \right)$ (A1)

correct sector area

eg $\,\,\,\,\,$ $\frac{1}{2}(8)(8)(1.70),{\text{ }}\frac{{97.1807}}{{360}}(64\pi ),{\text{ }}54.2759$ (A1)

area of triangle (seen anywhere) (A1)

eg $\,\,\,\,\,$ $\frac{1}{2}(8)(8)\sin 1.70,{\text{ }}\frac{1}{2}(8)(12)\sin 0.722,{\text{ }}\frac{1}{2} \times \sqrt {64 - 36} \times 12,{\text{ }}31.7490$

appropriate approach (seen anywhere) (M1)

eg $\,\,\,\,\,$ ${A_{{\text{triangle}}}} - {A_{{\text{sector}}}}$ , their sector-their triangle

22.5269

area of shaded region $= 22.5{\text{ }}({\text{c}}{{\text{m}}^2})$ A1 N4

Note: Award M0A0A0A0A1 then M1A0 (if appropriate) for correct triangle area without any attempt to find an angle in triangle OAB.

[7 marks]

Examiners report

[N/A]

The vector equation of line $L$ is given by r $= \left( {\begin{array}{*{20}{c}} { - 1} \\ 3 \\ 8 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 4 \\ 5 \\ { - 1} \end{array}} \right)$ .

Point P is the point on $L$ that is closest to the origin. Find the coordinates of P.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

METHOD 1 (Distance between the origin and P)

correct position vector for OP (A1)

eg $\overrightarrow {{\text{OP}}} = \left( {\begin{array}{*{20}{c}} { - 1 + 4t} \\ {3 + 5t} \\ {8 - t} \end{array}} \right)$ , ${\text{P}} = \left( { - 1 + 4t{\text{,}}\,\,3 + 5t{\text{,}}\,\,8 - t} \right)$

correct expression for OP or OP² (seen anywhere) A1

eg $\sqrt {{{\left( { - 1 + 4t} \right)}^2} + {{\left( {3 + 5t} \right)}^2} + {{\left( {8 - t} \right)}^2}}$ , ${\left( { - 1 + 4x} \right)^2} + {\left( {3 + 5x} \right)^2} + {\left( {8 - x} \right)^2}$

valid attempt to find the minimum of OP (M1)

eg $d' = 0$ , root on sketch of $d^{'}$ , min indicated on sketch of $d$

$t = - \frac{1}{{14}}{\text{,}}\,\, - 0.0714285$ (A1)

substitute their value of $t$ into $L$ (only award if there is working to find $t$ ) (M1)

eg one correct coordinate, $- 1 + 4\left( { - \frac{1}{{14}}} \right)$

$\left( { - 1.28571{\text{,}}\,\,2.64285{\text{,}}\,\,8.07142} \right)$

$\left( { - \frac{9}{7}{\text{,}}\,\,\frac{{37}}{{14}}{\text{,}}\,\,\frac{{113}}{{14}}} \right)\,\,\, = \left( { - 1.29{\text{,}}\,\,2.64{\text{,}}\,\,8.07} \right)$ A1 N2

METHOD 2 (Perpendicular vectors)

recognizing that closest implies perpendicular (M1)

eg $\overrightarrow {{\text{OP}}} \bot \,L$ (may be seen on sketch), $a \bullet b = 0$

valid approach involving $\overrightarrow {{\text{OP}}}$ (M1)

eg $\overrightarrow {{\text{OP}}} = \left( {\begin{array}{*{20}{c}} { - 1 + 4t} \\ {3 + 5t} \\ {8 - t} \end{array}} \right){\text{,}}\,\,\left( {\begin{array}{*{20}{c}} 4 \\ 5 \\ { - 1} \end{array}} \right) \bullet \overrightarrow {{\text{OP}}} {\text{,}}\,\,\left( {\begin{array}{*{20}{c}} 4 \\ 5 \\ { - 1} \end{array}} \right) \bot \overrightarrow {{\text{OP}}}$

correct scalar product A1

eg $4\left( { - 1 + 4t} \right) + 5\left( {3 + 5t} \right) - 1\left( {8 - t} \right)$ , $- 4 + 16t + 15 + 25t - 8 + t = 0$ , $42t + 3$

$t = - \frac{1}{{14}}{\text{,}}\,\, - 0.0714285$ (A1)

substitute their value of $t$ into $L$ or $\overrightarrow {{\text{OP}}}$ (only award if scalar product used to find $t$ ) (M1)

eg one correct coordinate, $- 1 + 4\left( { - \frac{1}{{14}}} \right)$

$\left( { - 1.28571{\text{,}}\,\,2.64285{\text{,}}\,\,8.07142} \right)$

$\left( { - \frac{9}{7}{\text{,}}\,\,\frac{{37}}{{14}}{\text{,}}\,\,\frac{{113}}{{14}}} \right)\,\,\, = \left( { - 1.29{\text{,}}\,\,2.64{\text{,}}\,\,8.07} \right)$ A1 N2

[6 marks]

Examiners report

[N/A]

A metal sphere has a radius 12.7 cm.

Find the volume of the sphere expressing your answer in the form $a \times {10^k}$ , $1 \leqslant a < 10$ and $k \in \mathbb{Z}$ .

[3]

The sphere is to be melted down and remoulded into the shape of a cone with a height of 14.8 cm.

Find the radius of the base of the cone, correct to 2 significant figures.

[3]

Markscheme

$\frac{4}{3}\pi {\left( {12.7} \right)^3}$ (or equivalent) A1

8580.24 (A1)

V = 8.58 × 10³ A1

[3 marks]

recognising volume of the cone is same as volume of their sphere (M1)

$\frac{1}{3}\pi {r^2}\,\left( {14.8} \right) =$ 8580.24 (or equivalent) A1

r = 23.529

r = 24 (cm) correct to 2 significant figures A1

[3 marks]

Examiners report

[N/A]

A rocket is travelling in a straight line, with an initial velocity of $140$ m s⁻¹. It accelerates to a new velocity of $500$ m s⁻¹ in two stages.

During the first stage its acceleration, $a$ m s⁻², after $t$ seconds is given by $a\left( t \right) = 240\,{\text{sin}}\left( {2t} \right)$ , where $0 \leqslant t \leqslant k$ .

The first stage continues for $k$ seconds until the velocity of the rocket reaches $375$ m s⁻¹.

Find an expression for the velocity, $v$ m s⁻¹, of the rocket during the first stage.

[4]

Find the distance that the rocket travels during the first stage.

[4]

During the second stage, the rocket accelerates at a constant rate. The distance which the rocket travels during the second stage is the same as the distance it travels during the first stage.

Find the total time taken for the two stages.

[6]

Markscheme

recognizing that $v = \int a$ (M1)

correct integration A1

eg $- 120\,{\text{cos}}\left( {2t} \right) + c$

attempt to find $c$ using their $v\left( t \right)$ (M1)

eg $- 120\,{\text{cos}}\left( 0 \right) + c = 140$

$v\left( t \right) = - 120\,{\text{cos}}\left( {2t} \right) + 260$ A1 N3

[4 marks]

evidence of valid approach to find time taken in first stage (M1)

eg graph, $- 120\,{\text{cos}}\left( {2t} \right) + 260 = 375$

$k = 1.42595$ A1

attempt to substitute their $v$ and/or their limits into distance formula (M1)

eg $\int_0^{1.42595} {\left| v \right|}$ , $\int {260 - 120} \,{\text{cos}}\left( {2t} \right)$ , $\int_0^k {\left( {260 - 120\,{\text{cos}}\left( {2t} \right)} \right)} \,{\text{d}}t$

$353.608$

distance is $354$ (m) A1 N3

[4 marks]

recognizing velocity of second stage is linear (seen anywhere) R1

eg graph, $s = \frac{1}{2}h\left( {a + b} \right)$ , $v = mt + c$

valid approach (M1)

eg $\int {v = 353.608}$

correct equation (A1)

eg $\frac{1}{2}h\left( {375 + 500} \right) = 353.608$

time for stage two $=0.808248$ ( $0.809142$ from 3 sf) A2

$2.23420$ ( $2.23914$ from 3 sf)

$2.23$ seconds ( $2.24$ from 3 sf) A1 N3

[6 marks]

Examiners report

[N/A]

The following diagram shows a right-angled triangle, ${\text{ABC}}$ , with ${\text{AC}} = 10\,{\text{cm}}$ , ${\text{AB}} = 6\,{\text{cm}}$ and ${\text{BC}} = 8\,{\text{cm}}$ .

The points ${\text{D}}$ and ${\text{F}}$ lie on $\left[ {{\text{AC}}} \right]$ .
$\left[ {{\text{BD}}} \right]$ is perpendicular to $\left[ {{\text{AC}}} \right]$ .
${\text{BEF}}$ is the arc of a circle, centred at ${\text{A}}$ .
The region $R$ is bounded by $\left[ {{\text{BD}}} \right]$ , $\left[ {{\text{DF}}} \right]$ and arc ${\text{BEF}}$ .

Find ${\text{B}}\widehat {\text{A}}{\text{C}}$ .

[2]

Find the area of $R$ .

[5]

Markscheme

correct working (A1)

eg ${\text{sin}}\,\alpha = \frac{8}{{10}}$ , ${\text{cos}}\,\theta = \frac{6}{{10}}$ , ${\text{cos}}\,{\text{B}}\widehat {\text{A}}{\text{C}} = \frac{{{6^2} + {{10}^2} - {8^2}}}{{2 \times 6 \times 10}}$

$0.927295$

${\text{B}}\widehat {\text{A}}{\text{C}} = 0.927$ $\left( { = 53.1^\circ } \right)$ (A1) N2

[2 marks]

Note: There may be slight differences in the final answer, depending on the approach the candidate uses in part (b). Accept a final answer that is consistent with their working.

correct area of sector ${\text{ABF}}$ (seen anywhere) (A1)

eg $\frac{1}{2} \times {6^2} \times 0.927$ , $\frac{{53.1301^\circ }}{{360^\circ }} \times \pi \times {6^2}$ , ${\text{16}}{\text{.6913}}$

correct expression (or value) for either $\left[ {{\text{AD}}} \right]$ or $\left[ {{\text{BD}}} \right]$ (seen anywhere) (A1)

eg ${\text{AD}} = 6\,{\text{cos}}\left( {{\text{B}}\widehat {\text{A}}{\text{C}}} \right)\,\,\,\left( { = 3.6} \right)$

${\text{BD}} = 6\,{\text{sin}}\left( {53.1^\circ } \right)\,\,\,\left( { = 4.8} \right)$

correct area of triangle ${\text{ABD}}$ (seen anywhere) (A1)

eg $\frac{1}{2} \times 6\,{\text{cos}}\,{\text{B}}\widehat {\text{A}}{\text{D}} \times 6\,{\text{sin}}\,{\text{B}}\widehat {\text{A}}{\text{D}}$ , $9\,{\text{sin}}\left( {{\text{2}}\,{\text{B}}\widehat {\text{A}}{\text{C}}} \right)$ , $8.64$ (exact)

appropriate approach (seen anywhere) (M1)

eg ${{\text{A}}_{{\text{triangle ABD}}}} - {{\text{A}}_{{\text{sector}}}}$ , their sector − their triangle ${\text{ABD}}$

$8.05131$

area of shaded region $= 8.05$ (cm²) A1 N2

[5 marks]

Examiners report

[N/A]

The following diagram shows a circle, centre O and radius $r$ mm. The circle is divided into five equal sectors.

N16/5/MATME/SP2/ENG/TZ0/03

One sector is OAB, and ${\rm{A\hat OB}} = \theta$ .

The area of sector AOB is $20\pi {\text{ m}}{{\text{m}}^2}$ .

Write down the exact value of $\theta$ in radians.

[1]

Find the value of $r$ .

[3]

Find AB.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\theta = \frac{{2\pi }}{5}$ A1 N1

[1 mark]

correct expression for area (A1)

eg $\,\,\,\,\,$ $A = \frac{1}{2}{r^2}\left( {\frac{{2\pi }}{5}} \right),{\text{ }}\frac{{\pi {r^2}}}{5}$

evidence of equating their expression to $20\pi$ (M1)

eg $\,\,\,\,\,$ $\frac{1}{2}{r^2}\left( {\frac{{2\pi }}{5}} \right) = 20\pi ,{\text{ }}{r^2} = 100,{\text{ }}r = \pm 10$

$r = 10$ A1 N2

[3 marks]

METHOD 1

evidence of choosing cosine rule (M1)

eg $\,\,\,\,\,$ ${a^2} = {b^2} + {c^2} - 2bc\cos A$

correct substitution of their $r$ and $\theta$ into RHS (A1)

eg $\,\,\,\,\,$ ${10^2} + {10^2} - 2 \times 10 \times 1{\text{0}}\cos \left( {\frac{{2\pi }}{5}} \right)$

11.7557

${\text{AB}} = 11.8{\text{ (mm)}}$ A1 N2

METHOD 2

evidence of choosing sine rule (M1)

eg $\,\,\,\,\,$ $\frac{{\sin A}}{a} = \frac{{\sin B}}{b}$

correct substitution of their $r$ and $\theta$ (A1)

eg $\,\,\,\,\,$ $\frac{{\sin \frac{{2\pi }}{5}}}{{{\text{AB}}}} = \frac{{\sin \left( {\frac{1}{2}\left( {\pi - \frac{{2\pi }}{5}} \right)} \right)}}{{10}}$

11.7557

${\text{AB}} = 11.8{\text{ (mm)}}$ A1 N2

[3 marks]

Examiners report

[N/A]

The following diagram shows a circle with centre $O$ and radius $1 cm$ . Points $A$ and $B$ lie on the circumference of the circle and $A \hat{O} B = 2 θ$ , where $0 < θ < \frac{π}{2}$ .

The tangents to the circle at $A$ and $B$ intersect at point $C$ .

Show that $AC = \tan θ$ .

[1]

Find the value of $θ$ when the area of the shaded region is equal to the area of sector $OADB$ .

[6]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct working for $AC$ (seen anywhere) A1

eg $\tan θ = \frac{AC}{OA}, \tan θ = \frac{AC}{1}$

$AC = \tan θ$ AG N0

[1 mark]

METHOD 1 (working with half the areas)

area of triangle $OAC$ or triangle $OBC$ (A1)

eg $\frac{1}{2} \times 1 \times \tan θ$

correct sector area (A1)

eg $\frac{1}{2} \times θ \times (1^{2}), \frac{1}{2} θ$

correct approach using their areas to find the shaded area (seen anywhere) (A1)

eg $A_{their triangle} - A_{their sector}, \frac{1}{2} θ - \frac{1}{2} \tan θ$

correct equation A1

eg $\frac{1}{2} \tan θ - \frac{1}{2} θ = \frac{1}{2} θ, \tan θ = 2 θ$

$1.16556$

$1.17$ A2 N4

METHOD 2 (working with entire kite and entire sector)

area of kite $OACB$ (A1)

eg $2 \times \frac{1}{2} \times 1 \times \tan θ, \frac{1}{2} \times \frac{1}{\cos θ} \times 2 \sin θ$

correct sector area (A1)

eg $\frac{1}{2} \times 2 θ \times (1^{2}), θ$

correct approach using their areas to find the shaded area (seen anywhere) (A1)

eg $A_{kite OACB} - A_{sector OADB}, θ - \tan θ$

correct equation A1

eg $\tan θ - θ = θ, \tan θ = 2 θ$

$1.16556$

$1.17$ A2 N4

[6 marks]

Examiners report

[N/A]

The following diagram shows the quadrilateral ABCD.

AB = 6.73 cm, BC = 4.83 cm, BĈD = 78.2° and CD = 3.80 cm.

Find BD.

[3]

The area of triangle ABD is 18.5 cm². Find the possible values of θ.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

choosing cosine rule (M1)

eg ${c^2} = {a^2} + {b^2} - 2ab\,{\text{cos}}\,C$

correct substitution into RHS (A1)

eg ${4.83^2} + {3.80^2} - 2 \times 4.83 \times 3.80 \times {\text{cos}}\,78.2$ , $30.2622$ ,

${4.83^2} + {3.80^2} - 2\left( {4.83} \right)\left( {3.80} \right) \times {\text{cos}}\,1.36$

5.50111

5.50 (cm) A1 N2

[3 marks]

correct substitution for area of triangle ABD (A1)

eg $\frac{1}{2} \times 6.73 \times 5.50111\,{\text{sin}}\,\theta$

correct equation A1

eg $\frac{1}{2} \times 6.73 \times 5.50111\,{\text{sin}}\,\theta = 18.5$ , ${\text{sin}}\,\theta = {\text{0}}{\text{.999393}}$

88.0023, 91.9976, 1.53593, 1.60566

θ = 88.0 (degrees) or 1.54 (radians)

θ = 92.0 (degrees) or 1.61 (radians) A1A1 N2

[4 marks]

Examiners report

[N/A]

The following diagram shows part of a circle with centre O and radius 4 cm.

Chord AB has a length of 5 cm and AÔB = θ.

Find the value of θ, giving your answer in radians.

[3]

Find the area of the shaded region.

[3]

Markscheme

METHOD 1

attempt to use the cosine rule (M1)

cos θ = $\frac{{{4^2} + {4^2} - {5^2}}}{{2 \times 4 \times 4}}$ (or equivalent) A1

θ = 1.35 A1

METHOD 2

attempt to split triangle AOB into two congruent right triangles (M1)

sin $\left( {\frac{\theta }{2}} \right) = \frac{{2.5}}{4}$ A1

θ = 1.35 A1

[3 marks]

attempt to find the area of the shaded region (M1)

$\frac{1}{2} \times 4 \times 4 \times \left( {2\pi - 1.35 \ldots } \right)$ A1

= 39.5 (cm²) A1

[3 marks]

Examiners report

[N/A]

Consider a triangle $ABC$ , where $AC = 12, CB = 7$ and $B \hat{A} C = 25 °$ .

Find the smallest possible perimeter of triangle $ABC$ .

Markscheme

EITHER

attempt to use cosine rule (M1)

$12^{2} + {AB}^{2} - 2 \times 12 \times \cos 25 ° \times AB = 7^{2}$ OR ${AB}^{2} - 21.7513 \dots AB + 95 = 0$ (A1)

at least one correct value for $AB$ (A1)

$AB = 6.05068 \dots$ OR $AB = 15.7007 \dots$

using their smaller value for $AB$ to find minimum perimeter (M1)

$12 + 7 + 6.05068 \dots$

attempt to use sine rule (M1)

$\frac{\sin B}{12} = \frac{\sin 25 °}{7}$ OR $\sin B = 0.724488 \dots$ OR $\hat{B} = 133.573 \dots °$ OR $\hat{B} = 46.4263 \dots °$ (A1)

at least one correct value for $C$ (A1)

$\hat{C} = 21.4263 \dots °$ OR $\hat{C} = 108.573 \dots °$

using their acute value for $\hat{C}$ to find minimum perimeter (M1)

$12 + 7 + \sqrt{12^{2} + 7^{2} - 2 \times 12 \times 7 \cos 21.4263 \dots °}$ OR $12 + 7 + \frac{7 \sin 21.4263 \dots °}{\sin 25 °}$

THEN

$25.0506 \dots$

minimum perimeter $= 25.1$ . A1

[5 marks]

Examiners report

[N/A]

Triangle ABC has a = 8.1 cm, b = 12.3 cm and area 15 cm². Find the largest possible perimeter of triangle ABC.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct substitution into the formula for area of a triangle (A1)

eg 15 = $\frac{1}{2}$ × 8.1 × 12.3 × sin C

correct working for angle C (A1)

eg sin C = 0.301114, 17.5245…, 0.305860

recognizing that obtuse angle needed (M1)

eg 162.475, 2.83573, cos C < 0

evidence of choosing the cosine rule (M1)

eg a² = b² + c² − 2bc cos(A)

correct substitution into cosine rule to find c (A1)

eg c² = (8.1)² + (12.3)² − 2(8.1)(12.3) cos C

c = 20.1720 (A1)

8.1 + 12.3 + 20.1720 = 40.5720

perimeter = 40.6 A1 N4

[7 marks]

Examiners report

[N/A]