Write your answer to part (b)(ii) in the form $a\times {10}^k$, where .

$3.91\times {10}^{-2}$    (A1)(ft)(A1)(ft)     (C2)

Note:     Answer should be consistent with their answer to part (b)(ii). Award (A1)(ft) for 3.91, and (A1)(ft) for ${10}^{-2}$. Follow through from part (b)(ii).

[2 marks]

Complete the second column of the table by giving one example of a number from each set.

Josh states: “Every integer is a natural number”.

Write down whether Josh’s statement is correct. Justify your answer.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(A1)(A1)(A1)(A1)(C4)

[4 marks]

Incorrect     (A1)

Natural numbers are positive integers. Integers can also be negative. (or equivalent)     (R1) (C2)

Note: Accept a correct justification. Do not award (R0)(A1).
Accept: a statement with an example of an integer which is not natural.

[2 marks]

Calculate the amount of money he has in the account after 5 years.

Write down the amount of interest he earned after 5 years.

Karl decides to donate this interest to a charity in France. The charity receives 170 euros (EUR). The exchange rate is 1 USD = t EUR.

Calculate the value of t.

$1000{\left(1+\frac{3.5}{4\times 100}\right)}^{4\times 5}$     (M1)(A1)

Note: Award (M1) for substitution in compound interest formula, (A1) for correct substitution.

OR

N = 5

I = 3.5

PV = 1000

P/Y = 1

C/Y = 4

Note: Award (A1) for C/Y = 4 seen, (M1) for other correct entries.

OR

N = 5 × 4

I = 3.5

PV = 1000

P/Y = 1

C/Y = 4

Note: Award (A1) for C/Y = 4 seen, (M1) for other correct entries.

= 1190.34 (USD)     (A1)

Note: Award (M1) for substitution in compound interest formula, (A1) for correct substitution.

[3 marks]

190.34 (USD)      (A1)(ft) (C4)

Note: Award (A1)(ft) for subtraction of 1000 from their part (a)(i). Follow through from (a)(i).

[1 mark]

$\frac{170}{190.34}$     (M1)

Note: Award (M1) for division of 170 by their part (a)(ii).

= 0.89     (A1)(ft) (C2)

Note: Follow through from their part (a)(ii).

[2 marks]

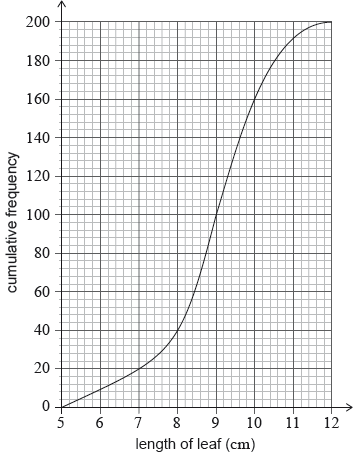
Write down the median length of these leaves.

Write down the number of leaves with a length less than or equal to 8 cm.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

9 (cm)     (A1)     (C1)

[1 mark]

40 (leaves)     (A1)     (C1)

[1 mark]

Calculate the time, in minutes, it takes for light from the Sun to reach the Earth.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{149600000}{300000\times 60}$     (M1)(M1)

Note:     Award (M1) for dividing the correct numerator (which can be presented in a different form such as $149.6\times {10}^6$ or $1.496\times {10}^8$) by $\text{300}\text{000}$ and (M1) for dividing by 60.

$=8.31(\text{minutes})(8.31111\dots \text{, 8 minutes 19 seconds})$     (A1)     (C3)

[3 marks]

Find the value of $a$.

Find the time, in years, for the population to decrease to 20 turtles.

There is a number $m$ beyond which the turtle population will not decrease.

Find the value of $m$. Justify your answer.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$55=a\times 2^0+10$   (M1)

Note: Award (M1) for correct substitution of zero and 55 into the function.

45      (A1)   (C2)  

[2 marks]

$45\times 2^{-t}+10⩽20$       (M1)

Note: Award (M1) for comparing correct expression involving 20 and their 45. Accept an equation.

$t=2.17$  (2.16992…)      (A1)(ft)   (C2)

Note: Follow through from their part (a), but only if positive.
Answer must be in years; do not accept months for the final (A1).  

[2 marks]

$m=$10       (A1)

because as the number of years increases the number of turtles approaches 10      (R1)   (C2)

Note: Award (R1) for a sketch with an asymptote at approximately $y=10$,
OR for table with values such as 10.003 and 10.001 for $t=14$ and $t=15$, for example,
OR when $t$ approaches large numbers $y$ approaches 10. Do not award (A1)(R0). 

[2 marks]

Write down the elements that belong to $A\cap B$.

Write down the elements that belong to $A\cap B^{\prime }$.

Write down $n\left(A\cap B^{\prime }\right)$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$A$ = {3, 6, 9, 12}  AND  $B$ = {2, 4, 6, 8, 10, 12, 14}      (M1)

Note: Award (M1) for listing all elements of sets $A$ and $B$. May be seen in part (b). Condone the inclusion of 15 in set $A$ when awarding the (M1).

6, 12     (A1)(A1)   (C3)  

Note: Award (A1) for each correct element. Award (A1)(A0) if one additional value seen. Award (A0)(A0) if two or more additional values are seen.

[3 marks]

3, 9     (A1)(ft)(A1)(ft)   (C2)  

Note: Follow through from part (a) but only if their $A$ and $B$ are explicitly listed.
Award (A1)(ft) for each correct element. Award (A1)(A0) if one additional value seen. Award (A0)(A0) if two or more additional values are seen.

[2 marks]

2     (A1)(ft)   (C1)  

Note: Follow through from part (b)(i).

[1 mark]

Place the numbers $2\pi \text{,}-5\text{,}{3}^{-1}$ and $2^{\frac{3}{2}}$ in the correct position on the Venn diagram.

In the table indicate which two of the given statements are true by placing a tick (✔) in the right hand column.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

    (A1)(A1)(A1)(A1)   (C4)

Note: Award (A1) for each number in the correct position.

[4 marks]

     (A1)(A1)   (C2)

Note: Award (A1) for each correctly placed tick.

[2 marks]

Calculate the radius of the base of the cone which has been removed.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\sqrt{{15}^2-{12}^2}$     (M1)

Note: Award (M1) for correct substitution into Pythagoras theorem.

OR

$\frac{\text{radius}}{21}=\frac{15}{35}$     (M1)

Note: Award (M1) for a correct equation.

= 9 (cm)     (A1) (C2)

[2 marks]

Write down the value of x.

Calculate the volume of the paperweight.

1 cm³ of glass has a mass of 2.56 grams.

Calculate the mass, in grams, of the paperweight.

3 (cm)    (A1) (C1)

[1 mark]

units are required in part (a)(ii)

$\frac{1}{2}\times \frac{4\pi \times {\left(3\right)}^3}{3}+3\times {\left(6\right)}^2$      (M1)(M1)

Note: Award (M1) for their correct substitution in volume of sphere formula divided by 2, (M1) for adding their correctly substituted volume of the cuboid.

= 165 cm³   (164.548…)      (A1)(ft) (C3)

Note: The answer is 165 cm³; the units are required. Follow through from part (a)(i).

[3 marks]

their 164.548… × 2.56      (M1)

Note: Award (M1) for multiplying their part (a)(ii) by 2.56.

= 421 (g)   (421.244…(g))      (A1)(ft) (C2)

Note: Follow through from part (a)(ii).

[2 marks]

Calculate the amount of MXN Harry received.

Calculate the value of the commission, in MXN, that Harry paid.

The exchange rate for this exchange was 1 USD = 17.24 MXN.

Calculate the amount of USD Harry received. Give your answer correct to the nearest cent.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

700 × 18.86      (M1)

Note: Award (M1) for multiplication by 18.86.

= 13 200 (13 202) (MXN)      (A1) (C2)

[2 marks]

2400 × 0.035       (M1)

Note: Award (M1) for multiplication by 0.035.

= 84 (MXN)     (A1) (C2)

[2 marks]

$\frac{2400-\text{their part (b)}}{17.24}$      (M1)

Note: Award (M1) for dividing 2400 minus their part (b), by 17.24. Follow through from part (b).

= 134.34 (USD)       (A1)(ft) (C2)

Note: Award at most (M1)(A0) if final answer is not given to nearest cent.

[2 marks]

Calculate the amount of VEF that Javier receives.

Calculate the total amount, in USD, that Javier has remaining from his 5000 USD after his trip to Venezuela.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

The first answer not given correct to two decimal places is not awarded the final (A1).

Incorrect rounding is not penalized thereafter.

$3000\times 6.3021$    (M1)

Note:     Award (M1) for multiplying 3000 by 6.3021.

$=18906.30$     (A1)     (C2)

[2 marks]

$\frac{18906.30-12000}{8.7268}\text{ + }(2000-1250)$    (M1)(M1)(M1)

Note:     Award (M1) for subtracting 12 000 from their answer to part (a) OR for 6906.30 seen, (M1) for dividing their amount by 8.7268 (can be implied if 791.389… seen) and (M1) for $2000-1250$ OR 750 seen.

$=1541.39$    (A1)(ft)     (C4)

Note:     Follow through from part (a).

[4 marks]

Use this exchange rate to calculate the amount of ARS that is equal to 350 AUD.

Calculate the total amount of ARS Jose paid to get 350 AUD.

Find the value of $x$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

Note:     In this question, the first time an answer is not to 2 dp the final (A1) is not awarded.

$\frac{350}{0.1559}$     (M1)

Note:     Award (M1) for dividing 350 by 0.1559.

$=2245.03\text{ (ARS)}$     (A1)     (C2)

[2 marks]

$2245.03\times 1.02$     (M1)

Note:     Award (M1) for multiplying their answer to part (a) by 1.02.

$=2289.93\text{ (ARS)}$     (A1)(ft)     (C2)

OR

$2245.03\times 0.02$     (M1)

Note:     Award (M1) for multiplying their answer to part (a) by 0.02.

$=44.9006$

$2245.03+44.90$

$=2289.93\text{ (ARS)}$     (A1)(ft)     (C2)

Note:     Follow through from part (a).

[2 marks]

$\frac{4228.38}{585}$     (M1)

Note:     Award (M1) for dividing 4228.38 by 585.

$=7.23$     (A1)     (C2)

[2 marks]

Complete the following table by placing ticks (✓) to show which of the number sets $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, and $\mathbb{R}$ these numbers belong to. The first row has been completed as an example.

Note: Award (A1) for each completely correct row, (A0) otherwise.

[6 marks]

Find the amount of Euros that Claudia receives. Give your answer correct to two decimal places.

Find the value of $r$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$8000\times 0.09819\times 0.98$     (M1)(M1)

Note:     Award (M1) for multiplying 8000 by 0.09819, (M1) for multiplying by 0.98 (or equivalent).

769.81 (EUR)     (A1)     (C3)

[3 marks]

$r\mathrm{\%}\times \frac{85}{0.08753}=14.57$     (M1)(M1)

Note:     Award (M1) for dividing 85 by 0.08753, and (M1) for multiplying their $\frac{85}{0.08753}$ by $r\mathrm{\%}$ and equating to 14.57.

OR

$\frac{85}{0.08753}=\text{971.095}\dots$     (M1)

Note:     Award (M1) for dividing 85 by 0.08753.

$\frac{14.57}{9.71095\dots }$$$OR$$$\frac{14.57}{971.095\dots }\times 100$     (M1)

Note:     Award (M1) for dividing 14.57 by 9.71095… or equivalent.

$r=1.50(1.50036\dots )$     (A1)     (C3)

[3 marks]

Calculate the amount that Velina receives in DKK.

Calculate the amount, in DKK, that will be left to exchange after commission.

Hence, calculate the amount of USD she receives.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

1200 × 7.0208       (M1)

Note: Award (M1) for multiplying by 7.0208.

8424.96 (DKK)       (A1) (C2)

[2 marks] 

0.95 × 3450       (M1)

Note: Award (M1) for multiplying 3450 by 0.95 (or equivalent).

3277.50 (DKK)       (A1) (C2)

Note: The answer must be given to two decimal places unless already penalized in part (a).

[2 marks] 

$\frac{3277.50}{7.0208}$      (M1)

Note: Follow through from part (b)(i). Award (M1) for dividing their part (b)(i) by 7.0208.

466.83 (USD)       (A1)(ft) (C2)

Note: The answer must be given to two decimal places unless already penalized in parts (a) or (b)(i).

[2 marks] 

Calculate the amount of PEN she receives.

Calculate the amount of USD she receives.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$(85-5)\times 3.25$     (M1)(M1)

Note:     Award (M1) for subtracting 5 from 85, (M1) for multiplying by 3.25.

Award (M1) for $85\times 3.25$, (M1) for subtracting $5\times 3.25$.

$=260\text{ (PEN)}$     (A1)     (C3)

[3 marks]

$\frac{(370\times 0.96)}{9.6}$     (M1)(M1)

Note:     Award (M1) for multiplying by 0.96 (or equivalent), (M1) for dividing by 9.6. If division by 3.25 seen in part (a), condone multiplication by 9.6 in part (b).

$=37\text{ (USD)}$     (A1)     (C3)

[3 marks]