For that day find how much weight was added after each lift.

For that day find the weight of Sergei’s first lift.

On that day, Sergei made 12 successive lifts. Find the total combined weight of these lifts.

5d = 46 − 21  OR  u₁ + 2d = 21  and  u₁ + 7d = 46     (M1)

Note: Award (M1) for a correct equation in d or for two correct equations in u₁ and d.

(d =) 5 (kg)      (A1) (C2)

[2 marks]

u₁ + 2 × 5 = 21    (M1)

OR

u₁ + 7 × 5 = 46    (M1)

Note: Award (M1) for substitution of their d into either of the two equations.

(u₁ =) 11 (kg)     (A1)(ft) (C2)

Note: Follow through from part (a)(i).

[2 marks]

$\frac{12}{2}\left(2\times 11+\left(12-1\right)\times 5\right)$     (M1)

Note: Award (M1) for correct substitution into arithmetic series formula.

= 462 (kg)     (A1)(ft) (C2)

Note: Follow through from parts (a) and (b).

[2 marks]

Write down the value of the common difference, $d$

Calculate the price of a ticket in the 16th row.

Find the total cost of buying 2 tickets in each of the first 16 rows.

($d$ =) − 250             A1

[1 mark]

$\left(u_{16}=\right)6800+\left(16-1\right)\left(-250\right)$           M1

(¥)3050           A1

[2 marks]

$\left(S_{16}=\right)\left(\frac{16}{2}\right)\left(2\times 6800+\left(16-1\right)\left(-250\right)\right)\times 2$          M1M1

Note: Award M1 for correct substitution into arithmetic series formula.
Award M1 for multiplication by 2 seen.

OR

$\left(S_{16}=\right)\left(\frac{16}{2}\right)\left(6800+3050\right)\times 2$         M1M1

Note: Award M1 for correct substitution into arithmetic series formula.
Award M1 for multiplication by 2 seen.

(¥)158 000 (157 600)          A1

[3 marks]

Write down the median length of these leaves.

Write down the number of leaves with a length less than or equal to 8 cm.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

9 (cm)     (A1)     (C1)

[1 mark]

40 (leaves)     (A1)     (C1)

[1 mark]

Find the common ratio of the sequence.

Find the volume of the smallest slice of pie.

The apple pie has a volume of $61 425 {\text{cm}}^3$.

Find the total number of slices Mia can cut from this pie.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$u_{1}r=30$  and  $u_1{r}^4=240,$       (M1)

Note: Award (M1) for both the given terms expressed in the formula for $u_n$.

OR

$30r^3=240 \left(r^3=8\right)$       (M1)

Note: Award (M1) for a correct equation seen.

$\left(r=\right) 2$       (A1)      (C2)

[2 marks]

$u_1\times 2=30$  OR  $u_1\times 2^4=240$       (M1)

Note: Award (M1) for their correct substitution in geometric sequence formula.

$\left(u_1=\right) 15$       (A1)(ft)      (C2)

Note: Follow through from part (a).

[2 marks]

$\frac{15\left(2^n-1\right)}{2-1}=61425$         (M1)

Note: Award (M1) for correctly substituted geometric series formula equated to $61425$.

$\left(n=\right) 12$  (slices)       (A1)(ft)      (C2)

Note: Follow through from parts (a) and (b).

[2 marks]

Find the $pH$ value for a solution in which the hydrogen ion concentration is $5.2\times {10}^{-8}$.

Write an expression for $C$ in terms of $pH$.

Find the hydrogen ion concentration in a solution with $pH 4.2$. Give your answer in the form $a\times 10k$ where $1\le a<10$ and $k$ is an integer.

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

$pH=-{\log }_{10}\left(5.2\times {10}^{-8}\right)=7.29 \left(7.28399\dots \right)$        (M1)A1

[2 marks]

$C={10}^{-pH}$     (M1)A1

Note: Award M1 for an exponential equation with $10$ as the base.

[2 marks]

$C={10}^{-4.2}=6.30957\dots \times {10}^{-5}$   (M1)

$6.31\times {10}^{-5}$        A1

[2 marks]

Show that the maximum height reached by the ball after it has bounced for the sixth time is $68 \text{cm}$, to the nearest $\text{cm}$.

Find the number of times, after the first bounce, that the maximum height reached is greater than $10 \text{cm}$.

Find the total vertical distance travelled by the ball from the point at which it is dropped until the fourth bounce.

use of geometric sequence with $r=0.85$        M1

EITHER

${\left(0.85\right)}^6\left(1.8\right)$   OR   $0.678869\dots$   OR   ${\left(0.85\right)}^5\left(1.53\right)$            A1

$=0.68 \text{m}$

$=68 \text{cm}$            AG

OR

${\left(0.85\right)}^6\left(180\right)$   OR   ${\left(0.85\right)}^5\left(153\right)$            A1

$=68 \text{cm}$            AG

[2 marks]

EITHER

${\left(0.85\right)}^n\left(1.8\right)>0.1$   OR   ${\left(0.85\right)}^{n-1}\left(1.53\right)>0.1$         (M1)

Note: If $1.8 \text{m}$ (or $180 \text{cm}$) is used then (M1) only awarded for use of $n$ in ${\left(0.85\right)}^n\left(1.8\right)>0.1$.
If $1.53 \text{m}$ (or $153 \text{cm}$) is used then (M1) only awarded for use of $n-1$ in ${\left(0.85\right)}^{n-1}\left(1.53\right)>0.1$.

$17$            A1

OR

${\left(0.85\right)}^{17}\left(1.8\right)=0.114 \text{m}$  and  ${\left(0.85\right)}^{18}\left(1.8\right)=0.0966 \text{m}$         (M1)

$17$            A1

OR

solving ${\left(0.85\right)}^n\left(1.8\right)=0.1$ to find $n=17.8$         (M1)

$17$            A1

Note: Evidence of solving may be a graph OR the “solver” function OR use of logs to solve the equation. Working may use $\text{cm}$.

[2 marks]

EITHER

distance (in one direction) travelled between first and fourth bounce

$=\frac{\left(1.8\times 0.85\right)\left(1-0.{85}^3\right)}{1-0.85} \left(=3.935925\dots \right)$         (A1)

recognizing distances are travelled twice except first distance         (M1)

$18+2\left(3.935925\right)$

$=9.67 \text{m} \left(9.67185\dots \text{m}\right)$            A1

OR

distance (in one direction) travelled between drop and fourth bounce

$=\frac{\left(1.8\right)\left(1-0.{85}^4\right)}{1-0.85} \left(=5.735925\dots \right)$         (A1)

recognizing distances are travelled twice except first distance         (M1)

$2\left(5.735925\right)-1.8$

$=9.67 \text{m} \left(9.67185\dots \text{m}\right)$            A1

OR

distance (in one direction) travelled between first and fourth bounce

$\left(0.85\right)\left(1.8\right)+{\left(0.85\right)}^2\left(1.8\right)+{\left(0.85\right)}^3\left(1.8\right) \left(=3.935925\dots \right)$         (A1)

recognizing distances are travelled twice except first distance        (M1)

$1.8+2\left(0.85\right)\left(1.8\right)+2{\left(0.85\right)}^2\left(1.8\right)+2{\left(0.85\right)}^3\left(1.8\right)$

$=9.67 \text{m} \left(9.67185\dots \text{m}\right)$            A1

Note: Answers may be given in $\text{cm}$.

[3 marks]

Most of the candidates who tackled this question effectively realized that they were dealing with a geometric sequence and were able to correctly identify the common ratio and identify the sixth term.

Many candidates misunderstood the instruction: ‘Find the number of times, after the first bounce…’ So, the incorrect answers of 16 or 18 were seen frequently.

Few candidates saw that they needed to calculate the distances identified by the seven dotted lines on the given diagram. Those that attempted the question often scored just one mark for using a correctly substituted formula determining the distance travelled in one direction.

For option 1, determine the minimum amount Juliana would need to invest. Give your answer to the nearest dollar.

For option 2, find the minimum value of $x$ that Juliana would need to invest each year. Give your answer to the nearest dollar.

METHOD 1 – (with $FV=\mathit{4000}$)

EITHER

$\text{N}=10$
$\text{I}=1.5$
$\text{FV}=4000$
$\text{P/Y}=1$
$\text{C/Y}=1$              (A1)(M1)

Note: Award A1 for $\left(3.5-2=\right) 1.5$ seen and M1 for all other entries correct.

OR

$4000=A{\left(1+0.015\right)}^{10}$              (A1)(M1)

Note: Award A1 for $1.5$ or $0.015$ seen, M1 for attempt to substitute into compound interest formula and equating to $4000$.

THEN

$\left(\text{PV}=\right) \$3447$            A1

Note: Award A0 if not rounded to a whole number or a negative sign given.

METHOD 2 – (With $FV$ including inflation)

calculate $\text{FV}$ with inflation

$4000\times 1.{02}^{10}$              (A1)

$\left(=4875.977\dots \right)$

EITHER

$4000\times 1.{02}^{10}=\text{PV}\times 1.{035}^{10}$                (M1)

OR

$\text{N}=10$
$\text{I}=3.5$
$\text{FV}=4875.977\dots$
$\text{P/Y}=1$
$\text{C/Y}=1$                (M1)

Note: Award M1 for their $\text{FV}$ and all other entries correct.

THEN

$\left(\text{PV}=\right) \$3457$            A1

Note: Award A0 if not rounded to a whole number or a negative sign given.

METHOD 3 – (Using formula to calculate real rate of return)

(real rate of return =) $1.47058\dots \left(\%\right)$              (A1)

EITHER

$4000=\text{PV}\times 1.0147058{\dots }^{10}$              (A1)

OR

$\text{N}=10$
$\text{I}=1.47058\dots$
$\text{FV}=4000$
$\text{P/Y}=1$
$\text{C/Y}=1$                (M1)

Note: Award M1 for all entries correct.

THEN

$\left(\text{PV}=\right) \$3457$            A1

[3 marks]

METHOD 1 – (Finding the future value of the investment using $PV$ from part (a))

$\text{N}=10$
$\text{I}=3.5$
$\text{PV}=3446.66\dots$ (from Method 1)  OR  $3456.67\dots$ (from Methods 2, 3)
$\text{P/Y}=1$
$\text{C/Y}=1$              (M1)

Note: Award M1 for interest rate $3.5$and answer to part (a) as $\text{PV}$.

$\left(\text{FV}=\right) \$4861.87$   OR   $\$4875.97$              (A1)

so payment required (from TVM) will be $\$294$   OR  $\$295$              A1

Note: Award A0 if a negative sign given, unless already penalized in part (a).

METHOD 2 – (Using $FV$)

$\text{N}=10$
$\text{I}=3.5$
$\text{PV}=-1000$
$\text{FV}=4875.977\dots$
$\text{P/Y}=1$
$\text{C/Y}=1$              (A1)(M1)

Note: Award A1 for $\text{I}=3.5$ and $\text{FV}=\pm 4875.977\dots$, M1 for all other entries correct and opposite $\text{PV}$ and $\text{FV}$ signs.

$\left(\text{PMT}=\right) \$295 \left(295.393\right)$              A1

Note: Correct 3sf answer is $295$, however accept an answer of $296$ given that the context supports rounding up. Award A0 if a negative sign given, unless already penalized in part (a).

[3 marks]

Very few candidates appeared to be familiar with real rate of return on an investment and attempted the question by ignoring the inflation rate. There was a mix of candidates who attempted to use the financial app on their graphic display calculator and those who attempted to use the compound interest formula, both of which are accepted methods. The preferred method of the IB for calculating the real rate of return is by simply subtracting the inflation rate from the nominal interest rate, however the exact formula is of course accepted too.

Was very poorly done, both in recognition of an appropriate future value with inflation and realizing that PV and FV must have opposite signs when using the financial app on their graphic display calculator. In both parts of the question, there seemed to be little consideration as to the appropriateness of the answers, and often unreasonable answers were presented.

Write down three equations that express the information given above.

Find the number of each type of ticket sold.

$x+y+z=600$           A1

$15x+10y+12z=7816$           A1

$x=2y$           A1

Note: Condone other labelling if clear, e.g. $a$ (adult), $c$ (child) and $s$ (student). Accept equivalent, distinct equations e.g. $2y+y+z=600$.

[3 marks]

$x=308, y=154, z=138$           A1A1

 
Note: Award A1 for all three correct values seen, A1 for correctly labelled as $x, y$ or $z$.
Accept answers written in words: e.g. $308$ adult tickets.

[2 marks]

Many candidates had at least two of the three equations written down correctly. The interpretation of the phrase “twice as many adult tickets sold as child tickets” was enigmatic. Consequently, $2x=y$ was a popular but erroneous answer.

Too many candidates spent considerable time attempting to solve three equations with three unknowns by hand with pages of working rather than using their GDC.

Find the value of $a$.

Find the value of $b$.

Given $0<M<8$, find the range for $N$.

Find the expected length of time between this earthquake and the next earthquake of at least this magnitude. Give your answer to the nearest year.

${\log }_{10} 100=a-3$        (M1)

$a=5$             A1

[2 marks]

EITHER

$N={10}^{5-M}$        (M1)

$=\frac{{10}^5}{{10}^M}\left(=\frac{100000}{{10}^M}\right)$

OR

$100=\frac{b}{{10}^3}$        (M1)

THEN

$b=100000 \left(={10}^5\right)$             A1

[2 marks]

$0.001<N<100000 \left({10}^{-3}<N<{10}^5\right)$             A1A1

Note: Award A1 for correct endpoints and A1 for correct inequalities/interval notation.

[2 marks]

$N=\frac{{10}^5}{{10}^{7.2}} \left(=0.0063095\dots \right)$             (M1)

length of time $=\frac{1}{0.0063095\dots }={10}^{2.2}$

$=158$ years             A1

[2 marks]

Many candidates did not attempt this question. Of those who did attempt the question, most of these candidates arrived at the correct answer to this part with the most common incorrect answer being 103.

Those that were successful in part (a) answered this well.

This was only answered correctly by the strongest candidates.

This part of the question was a discriminator as correct responses were few and far between.

Find the common difference.

Find the tenth term.

Find the sum of the first ten terms.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

subtracting terms     (M1)

eg$$$5-8,u_2-u_1$

$d=-3$     A1     N2

[2 marks]

correct substitution into formula     (A1)

eg$$$u_{10}=8+(10-1)(-3),8-27,-3(10)+11$

$u_{10}=-19$     A1     N2

[2 marks]

correct substitution into formula for sum     (A1)

eg$$$S_{10}=\frac{10}{2}(8-19),\text{ 5}\left(2(8)+(10-1)(-3)\right)$

$S_{10}=-55$     A1     N2

[2 marks]

Calculate the pH of the coffee.

Determine whether the unknown liquid is more or less acidic than the coffee. Justify your answer mathematically.

(pH =)$-{\log }_{10}\left(1.3\times {10}^{-5}\right)$           (M1)

$4.89 \left(4.88605\dots \right)$           A1

[2 marks]

EITHER

calculating pH

(pH =)$-{\log }_{10}\left(10\times 1.3\times {10}^{-5}\right)$           (M1)

$3.89 \left(3.88605\dots \right)$           A1

($3.89<4.89$, therefore) the unknown liquid is more acidic (than coffee).           A1

Note: Follow through within the part for the final A1. A correct conclusion must be supported by a mathematical justification linking the $C$-value to the pH level to earn the final A1; a comparison of $C$-values only earns M0A0A0.

OR

referencing the graph

The graph of $y=-{\log }_{10} \left(x\right)$ shows that as the value of $x$ increases, the value of $y$ decreases.         M1

Since the $C$-value ($x$-value) of the unknown liquid is larger than that of the coffee, the pH level ($y$-value) is lower.         R1

The unknown liquid is more acidic (than coffee).         A1

Note: Follow through within the part for the final A1. A correct conclusion must be supported by a mathematical justification linking the $C$-value to the pH level to earn the final A1; a comparison of $C$-values only earns M0R0A0.

[3 marks]

Evaluation of logarithms was well done, although the notation when substituting into the logarithmic formula was not always correct, with several candidates including a multiplication sign between the base and the argument. Even when the substitution was done correctly, some candidates still used multiplication, so not fully understanding logarithmic notation.

Several candidates multiplied their answer to part (a) by 10 rather than multiplying the C-value by 10, and several attempted to compare the C-values rather than calculating the pH of the unknown liquid. Most were able to make a correct contextual interpretation of their result.

Find the amount they will pay the bank each month.

Find the amount Raul and Rosy will still owe the bank at the end of the first $10$ years.

Using your answers to parts (a) and (b)(i), calculate how much interest they will have paid in total during the first $10$ years.

$N=360$
$I\%=3.8$
$PV=\left(\pm \right)170 000$
$FV=0$
$P/Y=12$
$C/Y=12$            (M1)(A1)

Note: Award (M1) for an attempt to use a financial app in their technology with at least two entries seen, award A1 for all entries correct. Accept a positive or negative value for $PV$.

$\left(PMT=\right) 792.13 \text{AUD}$             A1

Note: Accept an answer of $-792.13$. Do not award final A1 if answer is not given correct to $2$ dp.

[3 marks]

$N=120$
$I\%=3.8$
$PV=\left(\pm \right)170 000$
$PMT=\left(\mp \right)792.13$
$P/Y=12$
$C/Y=12$            (M1)(A1)

Note: Award (M1) for an attempt to use a financial app in their technology with at least two entries seen, award A1 for all entries correct. $PV$ and $PMT$ must have opposite signs.

$\left(FV=\right) 133019.94 \text{AUD}$             A1

Note: Do not award final A1 if answer is not given correct to $2$ dp, unless already penalized in part (a). Accept $133020.30$ from use of exact value for $\mathrm{PMT}$.

[3 marks]

amount of money paid: $120\times 792.13 (=95055.60)$             (M1)

loan paid off: $170 000-133019.94 \left(=36980.06\right)$             (M1)

interest paid: $(95055.60-36980.06=) 58075.54$  $\text{AUD}$             A1

Note: Allow $58075.60$ or $58075.90$ from use of some exact values from parts (a) and (b)(i). If their answer to part (b)(i) is greater than $170 000$ then award at most (M1)(M1)(A0) for follow through in part (b)(ii).

[3 marks]

This question was quite challenging for many candidates. In part (a), it was commendable that a significant minority of candidates arrived at the required answer, but others simply used $N=30$ or attempted to use the compound interest formula. Candidates were not using their GDC efficiently. Those candidates who showed their calculator entries could score at least one mark out of three for communicating their method. For those candidates who were comfortable with the financial application in their GDC in parts (a) and (b)(i), five out of six marks was a popular score. Some neglected to round their answers to two decimal places as required. Part (c) proved to be particularly difficult for candidates to decipher which values were necessary to find the amount of interest paid. Most candidates scored only one mark for the amount of money paid over the ten years. Many incorrect or unnecessary calculations were shown. Some candidates attempted to find an interest rate.

This question was quite challenging for many candidates. In part (a), it was commendable that a significant minority of candidates arrived at the required answer, but others simply used $N=30$ or attempted to use the compound interest formula. Candidates were not using their GDC efficiently. Those candidates who showed their calculator entries could score at least one mark out of three for communicating their method. For those candidates who were comfortable with the financial application in their GDC in parts (a) and (b)(i), five out of six marks was a popular score. Some neglected to round their answers to two decimal places as required. Part (c) proved to be particularly difficult for candidates to decipher which values were necessary to find the amount of interest paid. Most candidates scored only one mark for the amount of money paid over the ten years. Many incorrect or unnecessary calculations were shown. Some candidates attempted to find an interest rate.

This question was quite challenging for many candidates. In part (a), it was commendable that a significant minority of candidates arrived at the required answer, but others simply used $N=30$ or attempted to use the compound interest formula. Candidates were not using their GDC efficiently. Those candidates who showed their calculator entries could score at least one mark out of three for communicating their method. For those candidates who were comfortable with the financial application in their GDC in parts (a) and (b)(i), five out of six marks was a popular score. Some neglected to round their answers to two decimal places as required. Part (c) proved to be particularly difficult for candidates to decipher which values were necessary to find the amount of interest paid. Most candidates scored only one mark for the amount of money paid over the ten years. Many incorrect or unnecessary calculations were shown. Some candidates attempted to find an interest rate.

Diagram $n$ is formed with 52 sticks. Find the value of $n$.

Find the total number of sticks used by Tomás for all 24 diagrams.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$4+3(n-1)=52$     (M1)(A1)

Note:     Award (M1) for substitution into the formula of the $n$th term of an arithmetic sequence, (A1) for correct substitution.

$n=17$     (A1)     (C3)

[3 marks]

$\frac{24}{2}(2\times 4+23\times 3)$$$OR$$$\frac{24}{2}(4+73)$     (M1)(A1)(ft)

Notes:     Award (M1) for substitution into the sum of the first $n$ terms of an arithmetic sequence formula, (A1)(ft) for their correct substitution, consistent with part (a).

924     (A1)(ft)     (C3)

Note:     Follow through from part (a).

[3 marks]

Write down the common ratio of the sequence.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{1}{2}(0.5)$     (A1)     (C1)

[1 mark]

Complete the second column of the table by giving one example of a number from each set.

Josh states: “Every integer is a natural number”.

Write down whether Josh’s statement is correct. Justify your answer.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(A1)(A1)(A1)(A1)(C4)

[4 marks]

Incorrect     (A1)

Natural numbers are positive integers. Integers can also be negative. (or equivalent)     (R1) (C2)

Note: Accept a correct justification. Do not award (R0)(A1).
Accept: a statement with an example of an integer which is not natural.

[2 marks]

Find the common ratio.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct use $\log x^n=n\log x$     A1

eg$$$16\ln x$

valid approach to find $r$     (M1)

eg$$$\frac{u_{n+1}}{u_n},\frac{\ln x^8}{\ln x^{16}},\frac{4\ln x}{8\ln x},\ln x^4=\ln x^{16}\times r^2$

$r=\frac{1}{2}$     A1     N2

[3 marks]

Calculate the value of Siân’s investment after four years. Give your answer correct to two decimal places.

After the four-year period, Siân withdraws $40000$ AUD from her savings account and uses this money to buy a car. It is known that the car will depreciate at a rate of $18$ % per year.

The value of the car will be $2500$ AUD after $t$ years.

Find the value of $t$.

$FV=50000{\left(1+\frac{5.6}{100\times 12}\right)}^{12\times 4}$       (M1)(A1)

Note: Award (M1) for substitution into compound interest formula, (A1) for correct substitution.

OR

$N=4$

$I\mathrm{\%}=5.6$

$PV=(\mp )50000$

$P\text{/}Y=1$

$C\text{/}Y=12$        (A1)(M1)

Note: Award (A1) for $C\text{/}Y=12$ seen, (M1) for all other correct entries.

OR

$N=48$

$I\mathrm{\%}=5.6$

$PV=(\mp )50000$

$P\text{/}Y=12$

$C\text{/}Y=12$        (A1)(M1)

Note: Award (A1) for $C\text{/}Y=12$ seen, (M1) for all other correct entries.

$\left(FV=\right)62520.97$ (AUD)        (A1)    (C3)

Note: The final (A1) is not awarded if the answer is not correct to 2 decimal places.

[3 marks]

$2500=40000{\left(1-\frac{18}{100}\right)}^t$   OR  $2500=40000{\left(0.82\right)}^{t-1}$       (M1)(A1)

Note: Award (M1) for substitution into compound interest formula or term of a geometric sequence formula and equating to $2500$, (A1) for correct substitution.

OR

$I\mathrm{\%}=-18$

$PV=(\pm )40000$

$FV=(\mp )2500$

$P\text{/}Y=1$

$C\text{/}Y=1$        (A1)(M1)

Note: Award (A1) for $FV=(\mp )2500$ seen, (M1) for all other correct entries. $PV$ and $FV$ must have opposite signs.

OR

$32800\text{, }26896\text{, }22054.72\text{, }18084.87\text{, }14829.59\text{, }\dots$       (M1)

$t_{13}=3031.38$  and  $t_{14}=2485.73$        (A1)

Note: Award (M1) for a list of at least $5$ correct terms beginning with $32800$, (A1) for identifying $t_{13}$ and $t_{14}$.

$(t=) 14.0 (13.9711\dots )$        (A1)    (C3)

[3 marks]

Find $r$.

Show that the sum of the infinite sequence is $4{\log }_{2}x$.

Find $d$, giving your answer as an integer.

Show that $S_{12}=12{\log }_{2}x-66$.

Given that $S_{12}$ is equal to half the sum of the infinite geometric sequence, find $x$, giving your answer in the form $2^p$, where $p\in \mathbb{Q}$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

evidence of dividing terms (in any order)     (M1)

eg$$$\frac{{\mu }_2}{{\mu }_1},\frac{2{\log }_{2}x}{{\log }_{2}x}$

$r=\frac{1}{2}$    A1     N2

[2 marks]

correct substitution     (A1)

eg$$$\frac{2{\log }_{2}x}{1-\frac{1}{2}}$

correct working     A1

eg$$$\frac{2{\log }_{2}x}{\frac{1}{2}}$

$S_{\mathrm{\infty }}=4{\log }_{2}x$     AG     N0

[2 marks]

evidence of subtracting two terms (in any order)     (M1)

eg$$$u_3-u_2,{\log }_{2}x-{\log }_2\frac{x}{2}$

correct application of the properties of logs     (A1)

eg$$${\log }_2\left(\frac{\frac{x}{2}}{x}\right),{\log }_2\left(\frac{x}{2}\times \frac{1}{x}\right),({\log }_{2}x-{\log }_{2}2)-{\log }_{2}x$

correct working     (A1)

eg$$${\log }_2\frac{1}{2},-{\log }_{2}2$

$d=-1$    A1     N3

[4 marks]

correct substitution into the formula for the sum of an arithmetic sequence     (A1)

eg$$$\frac{12}{2}\left(2{\log }_{2}x+(12-1)(-1)\right)$

correct working     A1

eg$$$6(2{\log }_{2}x-11),\frac{12}{2}(2{\log }_{2}x-11)$

$12{\log }_{2}x-66$    AG     N0

[2 marks]

correct equation     (A1)

eg$$$12{\log }_{2}x-66=2{\log }_{2}x$

correct working     (A1)

eg$$$10{\log }_{2}x=66,{\log }_{2}x=6.6,2^{66}=x^{10},{\log }_2\left(\frac{x^{12}}{x^2}\right)=66$

$x=2^{6.6}$ (accept $p=\frac{66}{10}$)     A1     N2

[3 marks]

Calculate the value of Imon’s investment after $5$ years.

At the end of the $5$ years, Imon withdrew $x \text{SGD}$ from the fixed deposit account and reinvested this into a super-savings account with a nominal annual interest rate of $5.7\%$, compounded half-yearly.

The value of the super-savings account increased to $20 000 \text{SGD}$ after $18$ months.

Find the value of $x$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\left(FV=\right) 25 000\times {\left(1+\frac{3.6}{100\times 12}\right)}^{12\times 5}$       (M1)(A1)

Note: Award (M1) for substituted compound interest formula, (A1) for correct substitutions.

OR

$N=5$
$I\%=3.6$
$PV=\mp 25 000$
$P/Y=1$
$C/Y=12$       (A1)(M1)

Note: Award (A1) for $C/Y=12$ seen, (M1) for all other correct entries.

OR

$N=60$
$I\%=3.6$
$PV=\mp 25 000$
$P/Y=12$
$C/Y=12$       (A1)(M1)

Note: Award (A1) for $C/Y=12$ seen, (M1) for all other correct entries.

$\left(FV=\right) 29 922 \left(\text{SGD}\right)$      (A1)   (C3)

Note: Do not award the final (A1) if answer is not given correct to the nearest integer.

[3 marks]

$20 000=PV\times {\left(1+\frac{5.7}{100\times 2}\right)}^{2\times 1.5}$       (M1)(A1)

Note: Award (M1) for substituted compound interest equated to $20 000$. Award (A1) for correct substitutions.

OR

$N=1.5$
$I\%=5.7$
$FV=\pm 20 000$
$P/Y=1$
$C/Y=2$       (A1)(M1)

Note: Award (A1) for $C/Y=2$ seen, (M1) for all other correct entries.

OR

$N=3$
$I\%=5.7$
$FV=\pm 20 000$
$P/Y=2$
$C/Y=2$       (A1)(M1)

Note: Award (A1) for $C/Y=2$ seen, (M1) for all other correct entries.

$\left(x=\right) 18 383 \left(\text{SGD}\right)$      (A1)   (C3)

Note: Do not award the final (A1) if answer is not given correct to the nearest integer (unless already penalized in part(a)).

[3 marks]

Find the distance from the base of this ladder to the top rung.

The company also makes a ladder that is 1050 cm long.

Find the maximum number of rungs in this 1050 cm long ladder.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$30+(11-1)\times 27$     (M1)(A1)

Note:     Award (M1) for substituted arithmetic sequence formula, (A1) for correct substitutions.

$=300\text{ (cm)}$     (A1)     (C3)

Note:     Units are not required.

[3 marks]

$1050⩾30+(n-1)\times 27$     (M1)(A1)(ft)

Note:     Award (M1) for substituted arithmetic sequence formula $⩽1050$, accept an equation, (A1) for correct substitutions.

$n=38$     (A1)(ft)     (C3)

Note:     Follow through from their 27 in part (a). The answer must be an integer and rounded down.

[3 marks]

Find u₈.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct working      (A1)

eg   −5 + (8 − 1)(3)

u₈ = 16     A1 N2

[2 marks]

Calculate the amount Yejin needs to have saved into her annuity fund, in order to meet her retirement goal.

Yejin has just turned 28 years old. She currently has no retirement savings. She wants to save part of her salary each month into her annuity fund.

Calculate the amount Yejin needs to save each month, to meet her retirement goal.

Use of finance solver           M1

N = 360, I = 5%, Pmt = 4000, FV = 0, PpY = 12, CpY = 1           A1

$755000 (correct to 3 s.f.)           A1

[3 marks]

N = 384, I = 5%, PV = 0, FV = 754638, PpY = 12, CpY = 1         M1A1

$817 per month (correct to 3 s.f.)          A1

[3 marks]

Find the common ratio.

Write down the second term of this sequence.

The sum of the first $k$ terms is greater than $2500$.

Find the smallest possible value of $k$.

$9=\left(\frac{8}{3}\right)r^3$      (M1)

Note: Award (M1) for correctly substituted geometric sequence formula equated to $9$.

$\left(r=\right)1.5\left(\frac{3}{2}\right)$         (A1) (C2)

[2 marks]

$4$         (A1)(ft)  (C1)

Note: Follow through from part (a).

[1 mark]

       (M1)

Note: Award (M1) for their correctly substituted geometric series formula compared to $2500$.

$k=15.2\left(15.17319\dots \right)$        (A1)(ft)

$\left(k=\right)16$        (A1)(ft)    (C3)

Note: Answer must be an integer for the final (A1)(ft) to be awarded.
Follow through from part (a).

[3 marks]

Write down the value of $\underset{i=1}{\overset{9}{\text{Σ}}}{u}_i$.

Find the value of $u_1$.

A game is played in which the arrow attached to the centre of the disc is spun and the sector in which the arrow stops is noted. If the arrow stops in sector $1$ the player wins $10$ points, otherwise they lose $2$ points.

Let $X$ be the number of points won

Find $\text{E}\left(X\right)$.

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

$360°$      A1 

[1 mark]

EITHER

$360=\frac{9}{2}\left(u_1+u_9\right)$        M1

$360=\frac{9}{2}\left(u_1+\frac{1}{3}{u}_1\right)=6u_1$        M1A1

OR

$360=\frac{9}{2}\left(2u_1+8d\right)$        M1

$u_9=\frac{1}{3}{u}_1=u_1+8d\Rightarrow u_1=-12d$        M1

Substitute this value $360=\frac{9}{2}\left(2u_1-8\times \frac{u_1}{12}\right) \left(=\frac{9}{2}\times \frac{4}{3}{u}_1=6u_1\right)$        A1

THEN

$u_1=60°$        A1

[4 marks]

$\text{E}\left(X\right)=10\times \frac{60}{360}-2\times \frac{300}{360}=0$        M1A1

[2 marks]

Write down the value of the iron in the form $a\times {10}^k$ where $1\le a<10 , k\in \mathrm{\mathbb{Z}}$.

Calculate James’s estimate of its volume, in ${\text{km}}^3$.

The actual volume of the asteroid is found to be $6.074\times {10}^6 {\text{km}}^3$.

Find the percentage error in James’s estimate of the volume.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$8.97\times {10}^{18} \left(\text{EUR}\right) \left(8.973\times {10}^{18}\right)$        (A1)(A1)  (C2)

Note: Award (A1) for $8.97 (8.973)$, (A1) for $\times {10}^{18}$. Award (A1)(A0) for $8.97\text{E}18$.
Award (A0)(A0) for answers of the type $8973\times {10}^{15}$.

[2 marks]

$\frac{4\times \mathrm{\pi }\times {113}^3}{3}$       (M1)

Note: Award (M1) for correct substitution in volume of sphere formula.

$6 040 000 \left({\text{km}}^3\right) \left(6.04\times {10}^6, \frac{5771588\mathrm{\pi }}{3}, 6 043 992.82\right)$       (A1)  (C2) 

[2 marks]

$\left|\frac{6 043 992.82-6.074\times {10}^6}{6.074\times {10}^6}\right|\times 100$       (M1)

Note: Award (M1) for their correct substitution into the percentage error formula (accept a consistent absence of “$\times {10}^6$” from all terms).

$0.494 \left(\%\right) \left(0.494026\dots \left(\%\right)\right)$       (A1)(ft)  (C2) 

Note: Follow through from their answer to part (b). If the final answer is negative, award at most (M1)(A0).

[2 marks]

Calculate the value of her savings after 10 years.

The rate of inflation during this 10 year period is 1.5% per year.

Calculate the real value of her savings after 10 years.

$2400{\left(1.04\right)}^{10}=\text{\$}3552.59$      M1A1

[2 marks]

real interest rate = $4-1.5=2.5\text{\% }$           A1

$2400{\left(1.025\right)}^{10}=\text{\$}3072.20$       M1A1

[3 marks]

Calculate the time, in minutes, it takes for light from the Sun to reach the Earth.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{149600000}{300000\times 60}$     (M1)(M1)

Note:     Award (M1) for dividing the correct numerator (which can be presented in a different form such as $149.6\times {10}^6$ or $1.496\times {10}^8$) by $\text{300}\text{000}$ and (M1) for dividing by 60.

$=8.31(\text{minutes})(8.31111\dots \text{, 8 minutes 19 seconds})$     (A1)     (C3)

[3 marks]

An orchestra has a sound intensity of 6.4 × 10⁻³W m⁻² . Calculate the intensity level, $L$ of the orchestra.

A rock concert has an intensity level of 112 dB. Find the sound intensity, $S$.

$10\text{lo}{\text{g}}_{10}\left(6.4\times {10}^{-3}\times {10}^{12}\right)$      (M1)

= 98.1(dB) (98.06179…)      A1

[2 marks]

$112=10\text{lo}{\text{g}}_{10}\left(S\times {10}^{12}\right)$     (M1)

0.158 (W m⁻²) (0.158489… (W m⁻²))      A1

[2 marks]

Find the value of her investment after a period of $5$ years.

Find an approximation for the real interest rate for the money invested in the account.

Hence find the real value of Sophia’s investment at the end of $5$ years.

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

Number of time periods $12\times 5=60$        (A1)

N = $60$
I% = $3.1$
PV = $0$
PMT = $200$
P/Y = $12$
C/Y = $12$
Value $\left(\$\right)12,961.91$        (M1)A1

[3 marks]

METHOD 1

Real interest rate $=3.1-2.0=1.1\%$        (M1)A1

METHOD 2

$\frac{1+0.031}{1+0.02}=1.01078\dots$        (M1)

$1.08\%$ (accept $1.1\%$)        A1

[2 marks]

N = $60$
I% = $1.1$
PV = $0$
PMT = $200$
P/Y = $12$
C/Y = $12$
$\left(\$\right)12,300 (12,330.33\dots )$      (M1)A1

Note: Award A1 for $\$12,300$ only.

[2 marks]

Let $p=c^2$ and $q=c^3$. Find the value of $\sum _{n=1}^{20}{u}_n$.

METHOD 1 (finding $u_1$ and d)

recognizing $\sum =S_{20}$ (seen anywhere)      (A1)

attempt to find $u_1$ or d using $\text{lo}{\text{g}}_c{c}^k=k$     (M1)
eg  $\text{lo}{\text{g}}_{c}c$, $\text{3}\text{lo}{\text{g}}_{c}c$, correct value of $u_1$ or d

$u_1$ = 2, d = 3 (seen anywhere)      (A1)(A1)

correct working     (A1)
eg  $S_{20}=\frac{20}{2}\left(2\times 2+19\times 3\right),S_{20}=\frac{20}{2}\left(2+59\right),10\left(61\right)$

$\sum _{n=1}^{20}{u}_n$ = 610     A1 N2

METHOD 2 (expressing S in terms of c)

recognizing $\sum =S_{20}$ (seen anywhere)      (A1)

correct expression for S in terms of c      (A1)
eg  $10\left(2\text{lo}{\text{g}}_c{c}^2+19\text{lo}{\text{g}}_c{c}^3\right)$

$\text{lo}{\text{g}}_c{c}^2=2,\text{lo}{\text{g}}_c{c}^3=3$  (seen anywhere)     (A1)(A1)

correct working      (A1)

eg  $S_{20}=\frac{20}{2}\left(2\times 2+19\times 3\right),S_{20}=\frac{20}{2}\left(2+59\right),10\left(61\right)$

$\sum _{n=1}^{20}{u}_n$ = 610     A1 N2

METHOD 3 (expressing S in terms of c)

recognizing $\sum =S_{20}$ (seen anywhere)      (A1)

correct expression for S in terms of c      (A1)
eg  $10\left(2\text{lo}{\text{g}}_c{c}^2+19\text{lo}{\text{g}}_c{c}^3\right)$

correct application of log law     (A1)
eg  $2\text{lo}{\text{g}}_c{c}^2=\text{lo}{\text{g}}_c{c}^4,19\text{lo}{\text{g}}_c{c}^3=\text{lo}{\text{g}}_c{c}^{57},10\left(\text{lo}{\text{g}}_c{\left(c^2\right)}^2+\text{lo}{\text{g}}_c{\left(c^3\right)}^{19}\right),10\left(\text{lo}{\text{g}}_c{c}^4+\text{lo}{\text{g}}_c{c}^{57}\right),10\left(\text{lo}{\text{g}}_c{c}^{61}\right)$

correct application of definition of log      (A1)
eg  $\text{lo}{\text{g}}_c{c}^{61}=61,\text{lo}{\text{g}}_c{c}^4=4,\text{lo}{\text{g}}_c{c}^{57}=57$

correct working     (A1)
eg  $S_{20}=\frac{20}{2}\left(4+57\right),10\left(61\right)$

$\sum _{n=1}^{20}{u}_n$ = 610     A1 N2

[6 marks]

The following diagram shows [AB], with length 2 cm. The line is divided into an infinite number of line segments. The diagram shows the first three segments.

The length of the line segments are $p\text{ cm},p^2\text{ cm},p^3\text{ cm},\dots$, where .

Show that $p=\frac{2}{3}$.

The following diagram shows [CD], with length $b\text{ cm}$, where $b>1$. Squares with side lengths $k\text{ cm},k^2\text{ cm},k^3\text{ cm},\dots$, where , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.

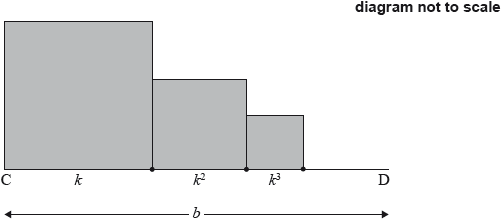
The total sum of the areas of all the squares is $\frac{9}{16}$. Find the value of $b$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

infinite sum of segments is 2 (seen anywhere)     (A1)

eg$$$p+p^2+p^3+\dots =2,\frac{u_1}{1-r}=2$

recognizing GP     (M1)

eg$$ratio is $p,\frac{u_1}{1-r},u_n=u_1\times r^{n-1},\frac{u_1(r^n-1)}{r-1}$

correct substitution into $S_{\mathrm{\infty }}$ formula (may be seen in equation)     A1

eg$$$\frac{p}{1-p}$

correct equation     (A1)

eg$$$\frac{p}{1-p}=2,p=2-2p$

correct working leading to answer     A1

eg$$$3p=2,2-3p=0$

$p=\frac{2}{3}\text{ (cm)}$     AG     N0

[5 marks]

recognizing infinite geometric series with squares     (M1)

eg$$$k^2+k^4+k^6+\dots ,\frac{k^2}{1-k^2}$

correct substitution into $S_{\mathrm{\infty }}=\frac{9}{16}$ (must substitute into formula)     (A2)

eg$$$\frac{k^2}{1-k^2}=\frac{9}{16}$

correct working     (A1)

eg$$$16k^2=9-9k^2,25k^2=9,k^2=\frac{9}{25}$

$k=\frac{3}{5}$ (seen anywhere)     A1

valid approach with segments and CD (may be seen earlier)     (M1)

eg$$$r=k,S_{\mathrm{\infty }}=b$

correct expression for $b$ in terms of $k$ (may be seen earlier)     (A1)

eg$$$b=\frac{k}{1-k},b=\sum _{n=1}^{\mathrm{\infty }}{k}^n,b=k+k^2+k^3+\dots$