IB Questionbank

Updates to Questionbank

User interface language: English | Español

SL Paper 2

Consider the function $f\left( x \right) = \frac{{27}}{{{x^2}}} - 16x,\,\,\,x \ne 0$ .

Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.

[4]

Use your graphic display calculator to find the zero of f (x).

[1]

b.i.

Use your graphic display calculator to find the coordinates of the local minimum point.

[2]

b.ii.

Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).

Give your answer in the form y = mx + c.

[2]

b.iii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(A1)(A1)(A1)(A1)

Note: Award (A1) for axis labels and some indication of scale; accept y or f(x).

Use of graph paper is not required. If no scale is given, assume the given window for zero and minimum point.

Award (A1) for smooth curve with correct general shape.

Award (A1) for x-intercept closer to y-axis than to end of sketch.

Award (A1) for correct local minimum with x-coordinate closer to y-axis than end of sketch and y-coordinate less than half way to top of sketch.

Award at most (A1)(A0)(A1)(A1) if the sketch intersects the y-axis or if the sketch curves away from the y-axis as x approaches zero.

[4 marks]

1.19 (1.19055…) (A1)

Note: Accept an answer of (1.19, 0).

Do not follow through from an incorrect sketch.

[1 mark]

b.i.

(−1.5, 36) (A1)(A1)

Note: Award (A0)(A1) if parentheses are omitted.

Accept x = −1.5, y = 36.

[2 marks]

b.ii.

y = −9.25x + 20.3 (y = −9.25x + 20.25) (A1)(A1)

Note: Award (A1) for −9.25x, award (A1) for +20.25, award a maximum of (A0)(A1) if answer is not an equation.

[2 marks]

b.iii.

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

b.iii.

A water container is made in the shape of a cylinder with internal height $h$ cm and internal base radius $r$ cm.

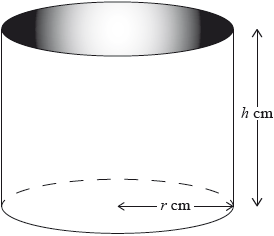
N16/5/MATSD/SP2/ENG/TZ0/06

The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.

The volume of the water container is $0.5{\text{ }}{{\text{m}}^3}$ .

The water container is designed so that the area to be coated is minimized.

One can of water-resistant material coats a surface area of $2000{\text{ c}}{{\text{m}}^2}$ .

Write down a formula for $A$ , the surface area to be coated.

[2]

Express this volume in ${\text{c}}{{\text{m}}^3}$ .

[1]

Write down, in terms of $r$ and $h$ , an equation for the volume of this water container.

[1]

Show that $A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ .

[2]

Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .

[3]

Using your answer to part (e), find the value of $r$ which minimizes $A$ .

[3]

Find the value of this minimum area.

[2]

Find the least number of cans of water-resistant material that will coat the area in part (g).

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$(A = ){\text{ }}\pi {r^2} + 2\pi rh$ (A1)(A1)

Note: Award (A1) for either $\pi {r^2}$ OR $2\pi rh$ seen. Award (A1) for two correct terms added together.

[2 marks]

$500\,000$ (A1)

Notes: Units not required.

[1 mark]

$500\,000 = \pi {r^2}h$ (A1)(ft)

Notes: Award (A1)(ft) for $\pi {r^2}h$ equating to their part (b).

Do not accept unless $V = \pi {r^2}h$ is explicitly defined as their part (b).

[1 mark]

$A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)$ (A1)(ft)(M1)

Note: Award (A1)(ft) for their ${\frac{{500\,000}}{{\pi {r^2}}}}$ seen.

Award (M1) for correctly substituting only ${\frac{{500\,000}}{{\pi {r^2}}}}$ into a correct part (a).

Award (A1)(ft)(M1) for rearranging part (c) to $\pi rh = \frac{{500\,000}}{r}$ and substituting for $\pi rh$ in expression for $A$ .

$A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ (AG)

Notes: The conclusion, $A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ , must be consistent with their working seen for the (A1) to be awarded.

Accept ${10^6}$ as equivalent to ${1\,000\,000}$ .

[2 marks]

$2\pi r - \frac{{{\text{1}}\,{\text{000}}\,{\text{000}}}}{{{r^2}}}$ (A1)(A1)(A1)

Note: Award (A1) for $2\pi r$ , (A1) for $\frac{1}{{{r^2}}}$ or ${r^{ - 2}}$ , (A1) for $- {\text{1}}\,{\text{000}}\,{\text{000}}$ .

[3 marks]

$2\pi r - \frac{{1\,000\,000}}{{{r^2}}} = 0$ (M1)

Note: Award (M1) for equating their part (e) to zero.

${r^3} = \frac{{1\,000\,000}}{{2\pi }}$ OR $r = \sqrt[3]{{\frac{{1\,000\,000}}{{2\pi }}}}$ (M1)

Note: Award (M1) for isolating $r$ .

sketch of derivative function (M1)

with its zero indicated (M1)

$(r = ){\text{ }}54.2{\text{ }}({\text{cm}}){\text{ }}(54.1926 \ldots )$ (A1)(ft)(G2)

[3 marks]

$\pi {(54.1926 \ldots )^2} + \frac{{1\,000\,000}}{{(54.1926 \ldots )}}$ (M1)

Note: Award (M1) for correct substitution of their part (f) into the given equation.

$= 27\,700{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}(27\,679.0 \ldots )$ (A1)(ft)(G2)

[2 marks]

$\frac{{27\,679.0 \ldots }}{{2000}}$ (M1)

Note: Award (M1) for dividing their part (g) by 2000.

$= 13.8395 \ldots$ (A1)(ft)

Notes: Follow through from part (g).

14 (cans) (A1)(ft)(G3)

Notes: Final (A1) awarded for rounding up their $13.8395 \ldots$ to the next integer.

[3 marks]

Examiners report

[N/A]

Let $f (x) = 4 - x^{3}$ and $g (x) = \ln x$ , for $x > 0$ .

Find $(f \circ g) (x)$ .

[2]

Solve the equation $(f \circ g) (x) = x$ .

[2]

b.i.

Hence or otherwise, given that $g (2 a) = f^{- 1} (2 a)$ , find the value of $a$ .

[3]

b.ii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to form composite (in any order) (M1)

eg $f (\ln x), g (4 - x^{3})$

$(f \circ g) (x) = 4 - {(\ln x)}^{3}$ A1 N2

[2 marks]

valid approach using GDC (M1)

eg , $(2.85, 2.85)$

$2.85056$

$2.85$ A1 N2

[2 marks]

b.i.

METHOD 1 – (using properties of functions)

recognizing inverse relationship (M1)

eg $f (g (2 a)) = f (f^{- 1} (2 a)) (= 2 a)$

equating $2 a$ to their $x$ from (i) (A1)

eg $2 a = 2.85056$

$1.42528$

$a = 1.43$ A1 N2

METHOD 2 – (finding inverse)

interchanging $x$ and $y$ (seen anywhere) (M1)

eg $x = 4 - y^{3}, f^{- 1} (x) = \sqrt[3]{4 - x}$

correct working (A1)

eg $\sqrt[3]{4 - 2 a} = \ln (2 a)$ , sketch showing intersection of $f^{- 1} (2 x)$ and $g (2 x)$

$1.42528$

$a = 1.43$ A1 N2

[3 marks]

b.ii.

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

The cross-sectional view of a tunnel is shown on the axes below. The line $[AB]$ represents a vertical wall located at the left side of the tunnel. The height, in metres, of the tunnel above the horizontal ground is modelled by $y = - 0.1 x^{3} + 0.8 x^{2}, 2 \leq x \leq 8$ , relative to an origin $O$ .

Point $A$ has coordinates $(2, 0)$ , point $B$ has coordinates $(2, 2.4)$ , and point $C$ has coordinates $(8, 0)$ .

When $x = 4$ the height of the tunnel is $6.4 m$ and when $x = 6$ the height of the tunnel is $7.2 m$ . These points are shown as $D$ and $E$ on the diagram, respectively.

Find $\frac{d y}{d x}$ .

[2]

a.i.

Hence find the maximum height of the tunnel.

[4]

a.ii.

Use the trapezoidal rule, with three intervals, to estimate the cross-sectional area of the tunnel.

[3]

Write down the integral which can be used to find the cross-sectional area of the tunnel.

[2]

c.i.

Hence find the cross-sectional area of the tunnel.

[2]

c.ii.

Markscheme

evidence of power rule (at least one correct term seen) (M1)

$\frac{d y}{d x} = - 0.3 x^{2} + 1.6 x$ A1

[2 marks]

a.i.

$- 0.3 x^{2} + 1.6 x = 0$ M1

$x = 5.33 (5.33333 \dots, \frac{16}{3})$ A1

$y = - 0.1 \times 5.33333 \dots^{3} + 0.8 \times 5.33333 \dots^{2}$ (M1)

Note: Award M1 for substituting their zero for $\frac{d y}{d x} (5.333 \dots)$ into $y$ .

$7.59 m (7.58519 \dots)$ A1

Note: Award M0A0M0A0 for an unsupported $7.59$ .
Award at most M0A0M1A0 if only the last two lines in the solution are seen.
Award at most M1A0M1A1 if their $x = 5.33$ is not seen.

[6 marks]

a.ii.

$A = \frac{1}{2} \times 2 ((2.4 + 0) + 2 (6.4 + 7.2))$ (A1)(M1)

Note: Award A1 for $h = 2$ seen. Award M1 for correct substitution into the trapezoidal rule (the zero can be omitted in working).

$= 29.6 m^{2}$ A1

[3 marks]

$A = \int_{2}^{8} - 0.1 x^{3} + 0.8 x^{2} d x$ OR $A = \int_{2}^{8} y d x$ A1A1

Note: Award A1 for a correct integral, A1 for correct limits in the correct location. Award at most A0A1 if $d x$ is omitted.

[2 marks]

c.i.

$A = 32.4 m^{2}$ A2

Note: As per the marking instructions, FT from their integral in part (c)(i). Award at most A1FTA0 if their area is $> 48$ , this is outside the constraints of the question (a $6 \times 8$ rectangle).

[2 marks]

c.ii.

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

c.i.

[N/A]

c.ii.

Urvashi wants to model the height of a moving object. She collects the following data showing the height, $h$ metres, of the object at time $t$ seconds.

She believes the height can be modeled by a quadratic function, $h\left( t \right) = a{t^2} + bt + c$ , where $a{\text{,}}\,\,b{\text{,}}\,\,c \in \mathbb{R}$ .

Hence find

Show that $4a + 2b + c = 34$ .

[1]

Write down two more equations for $a$ , $b$ and $c$ .

[3]

Solve this system of three equations to find the value of $a$ , $b$ and $c$ .

[4]

when the height of the object is zero.

[3]

d.i.

the maximum height of the object.

[2]

d.ii.

Markscheme

$t = 2{\text{,}}\,\,h = 34 \Rightarrow \,\,34 = a{2^2} + 2b + c$ M1

$\Rightarrow {\text{ }}34 = 4a + 2b + c$ AG

[1 mark]

attempt to substitute either (5, 38) or (7, 24) M1

$25a + 5b + c = 38$ A1

$49a + 7b + c = 24$ A1

[3 marks]

$a = - \frac{5}{3}{\text{,}}\,\,b = 13{\text{,}}\,\,c = \frac{{44}}{3}$ M1A1A1A1

[3 marks]

$- \frac{5}{3}{t^2} + 13t + \frac{{44}}{3} = 0$ M1

$t = 8.8$ seconds M1A1

[3 marks]

d.i.

attempt to find maximum height, e.g. sketch of graph M1

$h = 40.0$ metres A1

[2 marks]

d.ii.

Examiners report

[N/A]

d.i.

[N/A]

d.ii.

A wind turbine is designed so that the rotation of the blades generates electricity. The turbine is built on horizontal ground and is made up of a vertical tower and three blades.

The point $A$ is on the base of the tower directly below point $B$ at the top of the tower. The height of the tower, $AB$ , is $90 m$ . The blades of the turbine are centred at $B$ and are each of length $40 m$ . This is shown in the following diagram.

The end of one of the blades of the turbine is represented by point $C$ on the diagram. Let $h$ be the height of $C$ above the ground, measured in metres, where $h$ varies as the blade rotates.

Find the

The blades of the turbine complete $12$ rotations per minute under normal conditions, moving at a constant rate.

The height, $h$ , of point $C$ can be modelled by the following function. Time, $t$ , is measured from the instant when the blade $[BC]$ first passes $[AB]$ and is measured in seconds.

$h (t) = 90 - 40 \cos (72 t °), t \geq 0$

Looking through his window, Tim has a partial view of the rotating wind turbine. The position of his window means that he cannot see any part of the wind turbine that is more than $100 m$ above the ground. This is illustrated in the following diagram.

maximum value of $h$ .

[1]

a.i.

minimum value of $h$ .

[1]

a.ii.

Find the time, in seconds, it takes for the blade $[BC]$ to make one complete rotation under these conditions.

[1]

b.i.

Calculate the angle, in degrees, that the blade $[BC]$ turns through in one second.

[2]

b.ii.

Write down the amplitude of the function.

[1]

c.i.

Find the period of the function.

[1]

c.ii.

Sketch the function $h (t)$ for $0 \leq t \leq 5$ , clearly labelling the coordinates of the maximum and minimum points.

[3]

Find the height of $C$ above the ground when $t = 2$ .

[2]

e.i.

Find the time, in seconds, that point $C$ is above a height of $100 m$ , during each complete rotation.

[3]

e.ii.

At any given instant, find the probability that point $C$ is visible from Tim’s window.

[3]

f.i.

The wind speed increases. The blades rotate at twice the speed, but still at a constant rate.

At any given instant, find the probability that Tim can see point $C$ from his window. Justify your answer.

[2]

f.ii.

Markscheme

maximum $h = 130$ metres A1

[1 mark]

a.i.

minimum $h = 50$ metres A1

[1 mark]

a.ii.

$(60 \div 12 =) 5 seconds$ A1

[1 mark]

b.i.

$360 \div 5$ (M1)

Note: Award (M1) for $360$ divided by their time for one revolution.

$= 72 °$ A1

[2 marks]

b.ii.

(amplitude =) $40$ A1

[1 mark]

c.i.

(period $= \frac{360}{72} =$ ) $5$ A1

[1 mark]

c.ii.

Maximum point labelled with correct coordinates. A1

At least one minimum point labelled. Coordinates seen for any minimum points must be correct. A1

Correct shape with an attempt at symmetry and “concave up" evident as it approaches the minimum points. Graph must be drawn in the given domain. A1

[3 marks]

$h = 90 - 40 \cos (144 °)$ (M1)

$(h =) 122 m (122.3606 \dots)$ A1

[2 marks]

e.i.

evidence of $h = 100$ on graph OR $100 = 90 - 40 \cos (72 t)$ (M1)

$t$ coordinates $3.55 (3.54892 . . .)$ OR $1.45 (1.45107 . . .)$ or equivalent (A1)

Note: Award A1 for either $t$ -coordinate seen.

$= 2.10$ seconds $(2.09784 \dots)$ A1

[3 marks]

e.ii.

$5 - 2.09784 \dots$ (M1)

$\frac{(2.902153 \dots)}{5}$ (M1)

$0.580 (0.580430 \dots)$ A1

[3 marks]

f.i.

METHOD 1

changing the frequency/dilation of the graph will not change the proportion of time that point $C$ is visible. A1

$0.580 (0.580430 . . .)$ A1

METHOD 2

correct calculation of relevant found values

$\frac{(2.902153 \dots) / 2}{5 / 2}$ A1

$0.580 (0.580430 . . .)$ A1

Note: Award A0A1 for an unsupported correct probability.

[2 marks]

f.ii.

Examiners report

Judging by the responses in parts (a), (b) and (c), transferring and interpreting the information from a diagram is a skill that requires further nurturing. The amplitude should be expressed as a positive value. Overall, the sketch of $h (t)$ reflected the correct general shape. Common flaws included a lack of symmetry about the mean, 'concave up' not evident as the curve approached the minimum points, and the curve being drawn beyond the given domain. At least one correct pair of coordinates was seen, though some gave their answers inaccurately, suggesting they found an approximate solution using the "trace" feature in their GDC. Most were able to find the height of point $C$ when $t = 2$ and make an attempt to find a time at which point $C$ is at a height of $100 m$ . It was pleasing to see a number of candidates draw $h = 100$ on their sketch, which would no doubt have assisted the candidates in visualizing the solution. Part (f) proved to be a high-grade discriminator, with few attaining full marks. Premature rounding in part (f)(i) resulted in an inaccurate final answer. It is recommended that candidates retrieve and use unrounded values from previous calculations in their GDC. Though many recognized the probability was independent of the speed of rotation, most were not able to support their answer through a correct calculation or written explanation.

a.i.

a.ii.

b.i.

b.ii.

c.i.

c.ii.

e.i.

e.ii.

f.i.

f.ii.

The Texas Star is a Ferris wheel at the state fair in Dallas. The Ferris wheel has a diameter of $61.8 m$ . To begin the ride, a passenger gets into a chair at the lowest point on the wheel, which is $2.7 m$ above the ground, as shown in the following diagram. A ride consists of multiple revolutions, and the Ferris wheel makes $1.5$ revolutions per minute.

The height of a chair above the ground, $h$ , measured in metres, during a ride on the Ferris wheel can be modelled by the function $h (t) = - a \cos (b t) + d$ , where $t$ is the time, in seconds, since a passenger began their ride.

Calculate the value of

A ride on the Ferris wheel lasts for $12$ minutes in total.

For exactly one ride on the Ferris wheel, suggest

Big Tex is a $16.7$ metre-tall cowboy statue that stands on the horizontal ground next to the Ferris wheel.

^{[Source: Aline Escobar., n.d. Cowboy. [image online] Available at: https://thenounproject.com/search/?q=cowboy&i=1080130
This file is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)
https://creativecommons.org/licenses/by-sa/3.0/deed.en [Accessed 13/05/2021]. Source adapted.]}

There is a plan to relocate the Texas Star Ferris wheel onto a taller platform which will increase the maximum height of the Ferris wheel to $65.2 m$ . This will change the value of one parameter, $a$ , $b$ or $d$ , found in part (a).

$a$ .

[2]

a.i.

$b$ .

[2]

a.ii.

$d$ .

[2]

a.iii.

Calculate the number of revolutions of the Ferris wheel per ride.

[2]

an appropriate domain for $h (t)$ .

[1]

c.i.

an appropriate range for $h (t)$ .

[2]

c.ii.

By considering the graph of $h (t)$ , determine the length of time during one revolution of the Ferris wheel for which the chair is higher than the cowboy statue.

[3]

Identify which parameter will change.

[1]

e.i.

Find the new value of the parameter identified in part (e)(i).

[2]

e.ii.

Markscheme

an attempt to find the amplitude (M1)

$\frac{61.8}{2}$ OR $\frac{64.5 - 2.7}{2}$

$(a =) 30.9 m$ A1

Note: Accept an answer of $(a =) - 30.9 m$ .

[2 marks]

a.i.

(period $= \frac{60}{1.5} =$ ) $40 (s)$ (A1)

( $(b =) \frac{360 °}{40}$ )

$(b =) 9$ A1

Note: Accept an answer of $(b =) - 9$ .

[2 marks]

a.ii.

attempt to find $d$ (M1)

$(d =) 30.9 + 2.7$ OR $\frac{64.5 + 2.7}{2}$

$(d =) 33.6 m$ A1

[2 marks]

a.iii.

$12 \times 1.5$ OR $\frac{12 \times 60}{40}$ (M1)

$18$ (revolutions per ride) A1

[2 marks]

$0 \leq t \leq 720$ A1

[1 mark]

c.i.

$2.7 \leq h \leq 64.5$ A1A1

Note: Award A1 for correct endpoints of domain and A1 for correct endpoints of range. Award A1 for correct direction of both inequalities.

[2 marks]

c.ii.

graph of $h (t)$ and $y = 16.7$ OR $h (t) = 16.7$ (M1)

$6.31596 \dots$ and $33.6840 \dots$ (A1)

$27.4 (s) (27.3680 \dots)$ A1

[3 marks]

$d$ A1

[1 mark]

e.i.

EITHER

$d + 30.9 = 65.2$ (A1)

$65.2 - (61.8 + 2.7) = 0.7$ (A1)

$3.4$ (new platform height) (A1)

THEN

$(d =) 34.3 m$ A1

[2 marks]

e.ii.

Examiners report

Overall, this question was not well answered. Part (a) proved to be problematic for most candidates – hardly any candidates determined all three parameters correctly. The value of b was rarely found. Most candidates were able to find the number of revolutions in part (b). Only a small number of candidates were able to determine the domain and range in part (c) correctly. In part (d), a number of candidates understood that they needed to solve the equation $h (t) = 1.67$ , and gained the method mark, but very few candidates gained all three marks. In part (e), determining the parameter which would change proved challenging, and few were able to determine correctly how the parameter d would change.

a.i.

[N/A]

a.ii.

[N/A]

a.iii.

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

e.i.

[N/A]

e.ii.

A function $f$ is given by $f(x) = (2x + 2)(5 - {x^2})$ .

The graph of the function $g(x) = {5^x} + 6x - 6$ intersects the graph of $f$ .

Find the exact value of each of the zeros of $f$ .

[3]

Expand the expression for $f(x)$ .

[1]

b.i.

Find $f’(x)$ .

[3]

b.ii.

Use your answer to part (b)(ii) to find the values of $x$ for which $f$ is increasing.

[3]

Draw the graph of $f$ for $- 3 \leqslant x \leqslant 3$ and $- 40 \leqslant y \leqslant 20$ . Use a scale of 2 cm to represent 1 unit on the $x$ -axis and 1 cm to represent 5 units on the $y$ -axis.

[4]

Write down the coordinates of the point of intersection.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$- 1,{\text{ }}\sqrt 5 ,{\text{ }} - \sqrt 5$ (A1)(A1)(A1)

Note: Award (A1) for –1 and each exact value seen. Award at most (A1)(A0)(A1) for use of 2.23606… instead of $\sqrt 5$ .

[3 marks]

$10x - 2{x^3} + 10 - 2{x^2}$ (A1)

Notes: The expansion may be seen in part (b)(ii).

[1 mark]

b.i.

$10 - 6{x^2} - 4x$ (A1)(ft)(A1)(ft)(A1)(ft)

Notes: Follow through from part (b)(i). Award (A1)(ft) for each correct term. Award at most (A1)(ft)(A1)(ft)(A0) if extra terms are seen.

[3 marks]

b.ii.

$10 - 6{x^2} - 4x > 0$ (M1)

Notes: Award (M1) for their $f’(x) > 0$ . Accept equality or weak inequality.

$- 1.67 < x < 1{\text{ }}\left( { - \frac{5}{3} < x < 1,{\text{ }} - 1.66666 \ldots < x < 1} \right)$ (A1)(ft)(A1)(ft)(G2)

Notes: Award (A1)(ft) for correct endpoints, (A1)(ft) for correct weak or strict inequalities. Follow through from part (b)(ii). Do not award any marks if there is no answer in part (b)(ii).

[3 marks]

N17/5/MATSD/SP2/ENG/TZ0/05.d/M (A1)(A1)(ft)(A1)(ft)(A1)

Notes: Award (A1) for correct scale; axes labelled and drawn with a ruler.

Award (A1)(ft) for their correct $x$ -intercepts in approximately correct location.

Award (A1) for correct minimum and maximum points in approximately correct location.

Award (A1) for a smooth continuous curve with approximate correct shape. The curve should be in the given domain.

Follow through from part (a) for the $x$ -intercepts.

[4 marks]

$(1.49,{\text{ }}13.9){\text{ }}\left( {(1.48702 \ldots ,{\text{ }}13.8714 \ldots )} \right)$ (G1)(ft)(G1)(ft)

Notes: Award (G1) for 1.49 and (G1) for 13.9 written as a coordinate pair. Award at most (G0)(G1) if parentheses are missing. Accept $x = 1.49$ and $y = 13.9$ . Follow through from part (b)(i).

[2 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

A pan, in which to cook a pizza, is in the shape of a cylinder. The pan has a diameter of 35 cm and a height of 0.5 cm.

M17/5/MATSD/SP2/ENG/TZ1/04

A chef had enough pizza dough to exactly fill the pan. The dough was in the shape of a sphere.

The pizza was cooked in a hot oven. Once taken out of the oven, the pizza was placed in a dining room.

The temperature, $P$ , of the pizza, in degrees Celsius, °C, can be modelled by

$P(t) = a{(2.06)^{ - t}} + 19,{\text{ }}t \geqslant 0$

where $a$ is a constant and $t$ is the time, in minutes, since the pizza was taken out of the oven.

When the pizza was taken out of the oven its temperature was 230 °C.

The pizza can be eaten once its temperature drops to 45 °C.

Calculate the volume of this pan.

[3]

Find the radius of the sphere in cm, correct to one decimal place.

[4]

Find the value of $a$ .

[2]

Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.

[2]

Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.

[3]

In the context of this model, state what the value of 19 represents.

[1]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$(V = ){\text{ }}\pi \times {{\text{(17.5)}}^2} \times 0.5$ (A1)(M1)

Notes: Award (A1) for 17.5 (or equivalent) seen.

Award (M1) for correct substitutions into volume of a cylinder formula.

$= 481{\text{ c}}{{\text{m}}^3}{\text{ }}(481.056 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}153.125\pi {\text{ c}}{{\text{m}}^3})$ (A1)(G2)

[3 marks]

$\frac{4}{3} \times \pi \times {r^3} = 481.056 \ldots$ (M1)

Note: Award (M1) for equating their answer to part (a) to the volume of sphere.

${r^3} = \frac{{3 \times 481.056 \ldots }}{{4\pi }}{\text{ }}( = 114.843 \ldots )$ (M1)

Note: Award (M1) for correctly rearranging so ${r^3}$ is the subject.

$r = 4.86074 \ldots {\text{ (cm)}}$ (A1)(ft)(G2)

Note: Award (A1) for correct unrounded answer seen. Follow through from part (a).

$= 4.9{\text{ (cm)}}$ (A1)(ft)(G3)

Note: The final (A1)(ft) is awarded for rounding their unrounded answer to one decimal place.

[4 marks]

$230 = a{(2.06)^0} + 19$ (M1)

Note: Award (M1) for correct substitution.

$a = 211$ (A1)(G2)

[2 marks]

$(P = ){\text{ }}211 \times {(2.06)^{ - 5}} + 19$ (M1)

Note: Award (M1) for correct substitution into the function, $P(t)$ . Follow through from part (c). The negative sign in the exponent is required for correct substitution.

$= 24.7$ (°C) $(24.6878 \ldots$ (°C)) (A1)(ft)(G2)

[2 marks]

$45 = 211 \times {(2.06)^{ - t}} + 19$ (M1)

Note: Award (M1) for equating 45 to the exponential equation and for correct substitution (follow through for their $a$ in part (c)).

$(t = ){\text{ }}2.89711 \ldots$ (A1)(ft)(G1)

$174{\text{ (seconds) }}\left( {173.826 \ldots {\text{ (seconds)}}} \right)$ (A1)(ft)(G2)

Note: Award final (A1)(ft) for converting their ${\text{2.89711}} \ldots$ minutes into seconds.

[3 marks]

the temperature of the (dining) room (A1)

the lowest final temperature to which the pizza will cool (A1)

[1 mark]

Examiners report

[N/A]

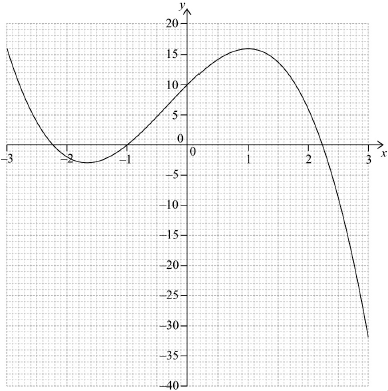
Consider the curve y = 2x³ − 9x² + 12x + 2, for −1 < x < 3

Sketch the curve for −1 < x < 3 and −2 < y < 12.

[4]

A teacher asks her students to make some observations about the curve.

Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.

State the name of the student who made an incorrect observation.

[1]

Find $\frac{{{\text{dy}}}}{{{\text{dx}}}}$ .

[3]

Given that y = 2x³ − 9x² + 12x + 2 = k has three solutions, find the possible values of k.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(A1)(A1)(A1)(A1)

Note: Award (A1) for correct window (condone a window which is slightly off) and axes labels. An indication of window is necessary. −1 to 3 on the x-axis and −2 to 12 on the y-axis and a graph in that window.
(A1) for correct shape (curve having cubic shape and must be smooth).
(A1) for both stationary points in the 1^st quadrant with approximate correct position,
(A1) for intercepts (negative x-intercept and positive y intercept) with approximate correct position.

[4 marks]

Rick (A1)

Note: Award (A0) if extra names stated.

[1 mark]

6x² − 18x + 12 (A1)(A1)(A1)

Note: Award (A1) for each correct term. Award at most (A1)(A1)(A0) if extra terms seen.

[3 marks]

6 < k < 7 (A1)(A1)(ft)(A1)

Note: Award (A1) for an inequality with 6, award (A1)(ft) for an inequality with 7 from their part (c) provided it is greater than 6, (A1) for their correct strict inequalities. Accept ]6, 7[ or (6, 7).

[3 marks]

Examiners report

[N/A]

At Grande Anse Beach the height of the water in metres is modelled by the function $h(t) = p\cos (q \times t) + r$ , where $t$ is the number of hours after 21:00 hours on 10 December 2017. The following diagram shows the graph of $h$ , for $0 \leqslant t \leqslant 72$ .

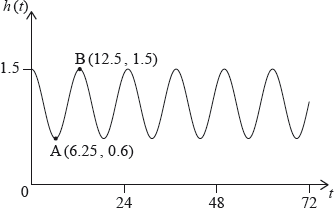
M17/5/MATME/SP2/ENG/TZ1/08

The point ${\text{A}}(6.25,{\text{ }}0.6)$ represents the first low tide and ${\text{B}}(12.5,{\text{ }}1.5)$ represents the next high tide.

How much time is there between the first low tide and the next high tide?

[2]

a.i.

Find the difference in height between low tide and high tide.

[2]

a.ii.

Find the value of $p$ ;

[2]

b.i.

Find the value of $q$ ;

[3]

b.ii.

Find the value of $r$ .

[2]

b.iii.

There are two high tides on 12 December 2017. At what time does the second high tide occur?

[3]

Markscheme

attempt to find the difference of $x$ -values of A and B (M1)

eg $\,\,\,\,\,$ $6.25 - 12.5{\text{ }}$

6.25 (hours), (6 hours 15 minutes) A1 N2

[2 marks]

a.i.

attempt to find the difference of $y$ -values of A and B (M1)

eg $\,\,\,\,\,$ $1.5 - 0.6$

$0.9{\text{ (m)}}$ A1 N2

[2 marks]

a.ii.

valid approach (M1)

eg $\,\,\,\,\,$ $\frac{{{\text{max}} - {\text{min}}}}{2},{\text{ }}0.9 \div 2$

$p = 0.45$ A1 N2

[2 marks]

b.i.

METHOD 1

period $= 12.5$ (seen anywhere) (A1)

valid approach (seen anywhere) (M1)

eg $\,\,\,\,\,$ ${\text{period}} = \frac{{2\pi }}{b},{\text{ }}q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{12.5}}$

0.502654

$q = \frac{{4\pi }}{{25}},{\text{ 0.503 }}\left( {{\text{or }} - \frac{{4\pi }}{{25}},{\text{ }} - 0.503} \right)$ A1 N2

METHOD 2

attempt to use a coordinate to make an equation (M1)

eg $\,\,\,\,\,$ $p\cos (6.25q) + r = 0.6,{\text{ }}p\cos (12.5q) + r = 1.5$

correct substitution (A1)

eg $\,\,\,\,\,$ $0.45\cos (6.25q) + 1.05 = 0.6,{\text{ }}0.45\cos (12.5q) + 1.05 = 1.5$

0.502654

$q = \frac{{4\pi }}{{25}},{\text{ }}0.503{\text{ }}\left( {{\text{or }} - \frac{{4\pi }}{{25}},{\text{ }} - 0.503} \right)$ A1 N2

[3 marks]

b.ii.

valid method to find $r$ (M1)

eg $\,\,\,\,\,$ $\frac{{{\text{max}} + {\text{min}}}}{2},{\text{ }}0.6 + 0.45$

$r = 1.05$ A1 N2

[2 marks]

b.iii.

METHOD 1

attempt to find start or end $t$ -values for 12 December (M1)

eg $\,\,\,\,\,$ $3 + 24,{\text{ }}t = 27,{\text{ }}t = 51$

finds $t$ -value for second max (A1)

$t = 50$

23:00 (or 11 pm) A1 N3

METHOD 2

valid approach to list either the times of high tides after 21:00 or the $t$ -values of high tides after 21:00, showing at least two times (M1)

eg $\,\,\,\,\,$ ${\text{21:00}} + 12.5,{\text{ 21:00}} + 25,{\text{ }}12.5 + 12.5,{\text{ }}25 + 12.5$

correct time of first high tide on 12 December (A1)

eg $\,\,\,\,\,$ 10:30 (or 10:30 am)

time of second high tide = 23:00 A1 N3

METHOD 3

attempt to set their $h$ equal to 1.5 (M1)

eg $\,\,\,\,\,$ $h(t) = 1.5,{\text{ }}0.45\cos \left( {\frac{{4\pi }}{{25}}t} \right) + 1.05 = 1.5$

correct working to find second max (A1)

eg $\,\,\,\,\,$ $0.503t = 8\pi ,{\text{ }}t = 50$

23:00 (or 11 pm) A1 N3

[3 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

b.iii.

[N/A]

Let $f(x) = {x^2} - 1$ and $g(x) = {x^2} - 2$ , for $x \in \mathbb{R}$ .

Show that $(f \circ g)(x) = {x^4} - 4{x^2} + 3$ .

[2]

On the following grid, sketch the graph of $(f \circ g)(x)$ , for $0 \leqslant x \leqslant 2.25$ .

M17/5/MATME/SP2/ENG/TZ2/06.b

[3]

The equation $(f \circ g)(x) = k$ has exactly two solutions, for $0 \leqslant x \leqslant 2.25$ . Find the possible values of $k$ .

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to form composite in either order (M1)

eg $\,\,\,\,\,$ $f({x^2} - 2),{\text{ }}{({x^2} - 1)^2} - 2$

$({x^4} - 4{x^2} + 4) - 1$ A1

$(f \circ g)(x) = {x^4} - 4{x^2} + 3$ AG N0

[2 marks]

M17/5/MATME/SP2/ENG/TZ2/06.b/M A1

A1A1 N3

Note: Award A1 for approximately correct shape which changes from concave down to concave up. Only if this A1 is awarded, award the following:

A1 for left hand endpoint in circle and right hand endpoint in oval,

A1 for minimum in oval.

[3 marks]

evidence of identifying max/min as relevant points (M1)

eg $\,\,\,\,\,$ $x = 0,{\text{ }}1.41421,{\text{ }}y = - 1,{\text{ }}3$

correct interval (inclusion/exclusion of endpoints must be correct) A2 N3

eg $\,\,\,\,\,$ $- 1 < k \leqslant 3,{\text{ }}\left] { - 1,{\text{ 3}}} \right],{\text{ }}( - 1,{\text{ }}3]$

[3 marks]

Examiners report

[N/A]

Consider the function $f(x) = 0.3{x^3} + \frac{{10}}{x} + {2^{ - x}}$ .

Consider a second function, $g(x) = 2x - 3$ .

Calculate $f(1)$ .

[2]

Sketch the graph of $y = f(x)$ for $- 7 \leqslant x \leqslant 4$ and $- 30 \leqslant y \leqslant 30$ .

[4]

Write down the equation of the vertical asymptote.

[2]

Write down the coordinates of the $x$ -intercept.

[2]

Write down the possible values of $x$ for which $x < 0$ and $f’(x) > 0$ .

[2]

Find the solution of $f(x) = g(x)$ .

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$0.3{(1)^3} + \frac{{10}}{1} + {2^{ - 1}}$ (M1)

Note: Award (M1) for correct substitution into function.

$= 10.8$ (A1)(G2)

[2 marks]

M17/5/MATSD/SP2/ENG/TZ1/03.b/M (A1)(A1)(A1)(A1)

Note: Award (A1) for indication of correct window and labelled axes.

Award (A1) for correct shape and position for $x < 0$ (with the local maximum, local minimum and $x$ -intercept in relative approximate location in ${{\text{3}}^{{\text{rd}}}}$ quadrant).

Award (A1) for correct shape and position for $x > 0$ (with the local minimum in relative approximate location in ${{\text{1}}^{{\text{st}}}}$ quadrant).

Award (A1) for smooth curve with indication of asymptote (graph should not touch $y$ -axis and should not curve away from the $y$ -axis). The asymptote is only assessed in this mark.

[4 marks]

$x = 0$ (A2)

Note: Award (A1) for “ $x = {\text{(a constant)}}$ ” and (A1) for “ ${\text{(a constant)}} = 0$ ”.

The answer must be an equation.

[2 marks]

$( - 6.18,{\text{ }}0){\text{ }}( - 6.17516 \ldots ,{\text{ }}0)$ (A1)(A1)

Note: Award (A1) for each correct coordinate. Award (A0)(A1) if parentheses are missing.

[2 marks]

$- 4.99 < x < - 2.47{\text{ }}( - 4.98688 \ldots < x < - 2.46635 \ldots )$ (A1)(A1)

Note: Award (A1) for both correct end points, (A1) for strict inequalities used with 2 endpoints.

[2 marks]

$0.3{x^3} + \frac{{10}}{x} + {2^{ - x}} = 2x - 3$ (M1)

Note: Award (M1) for equating the expressions for $f$ and $g$ or for the line $y = 2x - 3$ sketched (positive gradient, negative $y$ -intercept) on their graph from part (a).

$(x = ){\text{ }} - 1.34{\text{ }}( - 1.33650 \ldots )$ (A1)(G2)

Note: Award a maximum of (M1)(A0) or (G1) for coordinate pair seen as final answer.

[2 marks]

Examiners report

[N/A]

Consider the function $g(x) = {x^3} + k{x^2} - 15x + 5$ .

The tangent to the graph of $y = g(x)$ at $x = 2$ is parallel to the line $y = 21x + 7$ .

Find $g'(x)$ .

[3]

Show that $k = 6$ .

[2]

b.i.

Find the equation of the tangent to the graph of $y = g(x)$ at $x = 2$ . Give your answer in the form $y = mx + c$ .

[3]

b.ii.

Use your answer to part (a) and the value of $k$ , to find the $x$ -coordinates of the stationary points of the graph of $y = g(x)$ .

[3]

Find $g’( - 1)$ .

[2]

d.i.

Hence justify that $g$ is decreasing at $x = - 1$ .

[1]

d.ii.

Find the $y$ -coordinate of the local minimum.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$3{x^2} + 2kx - 15$ (A1)(A1)(A1)

Note: Award (A1) for $3{x^2}$ , (A1) for $2kx$ and (A1) for $- 15$ . Award at most (A1)(A1)(A0) if additional terms are seen.

[3 marks]

$21 = 3{(2)^2} + 2k(2) - 15$ (M1)(M1)

Note: Award (M1) for equating their derivative to 21. Award (M1) for substituting 2 into their derivative. The second (M1) should only be awarded if correct working leads to the final answer of $k = 6$ .

Substituting in the known value, $k = 6$ , invalidates the process; award (M0)(M0).

$k = 6$ (AG)

[2 marks]

b.i.

$g(2) = {(2)^3} + (6){(2)^2} - 15(2) + 5{\text{ }}( = 7)$ (M1)

Note: Award (M1) for substituting 2 into $g$ .

$7 = 21(2) + c$ (M1)

Note: Award (M1) for correct substitution of 21, 2 and their 7 into gradient intercept form.

$y - 7 = 21(x - 2)$ (M1)

Note: Award (M1) for correct substitution of 21, 2 and their 7 into gradient point form.

$y = 21x - 35$ (A1) (G2)

[3 marks]

b.ii.

$3{x^2} + 12x - 15 = 0$ (or equivalent) (M1)

Note: Award (M1) for equating their part (a) (with $k = 6$ substituted) to zero.

$x = - 5,{\text{ }}x = 1$ (A1)(ft)(A1)(ft)

Note: Follow through from part (a).

[3 marks]

$3{( - 1)^2} + 12( - 1) - 15$ (M1)

Note: Award (M1) for substituting $- 1$ into their derivative, with $k = 6$ substituted. Follow through from part (a).

$= - 24$ (A1)(ft) (G2)

[2 marks]

d.i.

$g’( - 1) < 0$ (therefore $g$ is decreasing when $x = - 1$ ) (R1)

[1 marks]

d.ii.

$g(1) = {(1)^3} + (6){(1)^2} - 15(1) + 5$ (M1)

Note: Award (M1) for correctly substituting 6 and their 1 into $g$ .

$= - 3$ (A1)(ft) (G2)

Note: Award, at most, (M1)(A0) or (G1) if answer is given as a coordinate pair. Follow through from part (c).

[2 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

d.i.

[N/A]

d.ii.

[N/A]

The diagram shows the straight line $L_{1}$ . Points $A (- 9, - 1)$ , $M (- 3, 2)$ and $C$ are points on $L_{1}$ .

$M$ is the midpoint of $AC$ .

Line $L_{2}$ is perpendicular to $L_{1}$ and passes through point $M$ .

The point $N (k, 4)$ is on $L_{2}$ .

Find the gradient of $L_{1}$ .

[2]

Find the coordinates of point $C$ .

[2]

Find the equation of $L_{2}$ . Give your answer in the form $a x + b y + d = 0$ , where $a, b, d \in ℤ$ .

[3]

Find the value of $k$ .

[2]

Find the distance between points $M$ and $N$ .

[2]

Given that the length of $AM$ is $\sqrt{45}$ , find the area of triangle $ANC$ .

[2]

Markscheme

$\frac{2 - (- 1)}{- 3 - (- 9)}$ (M1)

Note: Award (M1) for correct substitution into the gradient formula.

$= \frac{1}{2} (\frac{3}{6}, 0.5)$ (A1)(G2)

[2 marks]

$- 3 = \frac{- 9 + x}{2} (- 6 + 9 = x)$ and $2 = \frac{- 1 + y}{2} (4 + 1 = y)$ (M1)

Note: Award (M1) for correct substitution into the midpoint formula for both coordinates.

(M1)

Note: Award (M1) for a sketch showing the horizontal displacement from $M$ to $C$ is $6$ and the vertical displacement is $3$ and the coordinates at $M$ .

$- 3 + 6 = 3$ and $2 + 3 = 5$ (M1)

Note: Award (M1) for correct equations seen.

$(3, 5)$ (A1)(G1)(G1)

Note: Accept $x = 3, y = 5$ . Award at most (M1)(A0) or (G1)(G0) if parentheses are missing.

[2 marks]

gradient of the normal $= - 2$ (A1)(ft)

Note: Follow through from their gradient from part (a).

$y - 2 = - 2 (x + 3)$ OR $2 = - 2 (- 3) + c$ (M1)

Note: Award (M1) for correct substitution of $M$ and their gradient of normal into straight line formula.

$2 x + y + 4 = 0$ (accept integer multiples) (A1)(ft)(G3)

[3 marks]

$2 (k) + 4 + 4 = 0$ (M1)

Note: Award (M1) for substitution of $y = 4$ into their equation of normal line or substitution of $M$ and $(k, 4)$ into equation of gradient of normal.

$k = - 4$ (A1)(ft)(G2)

Note: Follow through from part (c).

[2 marks]

$\sqrt{{(- 4 + 3)}^{2} + {(4 - 2)}^{2}}$ (M1)

Note: Award (M1) for correctly substituting point $M$ and their $N$ into distance formula.

$\sqrt{5} (2.24, 2.23606 \dots)$ (A1)(ft)

Note: Follow through from part (d).

[2 marks]

$\frac{1}{2} \times (2 \times \sqrt{45}) \times \sqrt{5}$ (M1)

Note: Award (M1) for their correct substitution into area of a triangle formula. Award (M0) for their $\frac{1}{2} \times (\sqrt{45}) \times \sqrt{5}$ without any evidence of multiplication by $2$ to find length $AC$ . Accept any other correct method to find the area.

$15$ (A1)(ft)(G2)

Note: Accept $15.02637 \dots$ from use of a $3$ sf value for $\sqrt{5}$ . Follow through from part (e).

[2 marks]

Examiners report

[N/A]

Let $f\left( x \right) = 2\,{\text{sin}}\left( {3x} \right) + 4$ for $x \in \mathbb{R}$ .

Let $g\left( x \right) = 5f\left( {2x} \right)$ .

The function $g$ can be written in the form $g\left( x \right) = 10\,{\text{sin}}\left( {bx} \right) + c$ .

The range of $f$ is $k$ ≤ $f\left( x \right)$ ≤ $m$ . Find $k$ and $m$ .

[3]

Find the range of $g$ .

[2]

Find the value of $b$ and of $c$ .

[3]

c.i.

Find the period of $g$ .

[2]

c.ii.

The equation $g\left( x \right) = 12$ has two solutions where $\pi$ ≤ $x$ ≤ ${\frac{{4\pi }}{3}}$ . Find both solutions.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid attempt to find range (M1)

eg , max = 6 min = 2,

$2\,{\text{sin}}\left( {3 \times \frac{\pi }{6}} \right) + 4$ and $2\,{\text{sin}}\left( {3 \times \frac{\pi }{2}} \right) + 4$ , $2\left( 1 \right) + 4$ and $2\left( { - 1} \right) + 4$ ,

$k = 2$ , $m = 6$ A1A1 N3

[3 marks]

10 ≤ $y$ ≤ 30 A2 N2

[2 marks]

evidence of substitution (may be seen in part (b)) (M1)

eg $5\left( {2\,{\text{sin}}\left( {{\text{3}}\left( {2x} \right)} \right) + 4} \right)$ , ${{\text{3}}\left( {2x} \right)}$

$b = 6$ , $c = 20$ (accept $10\,{\text{sin}}\left( {6x} \right) + 20$ ) A1A1 N3

Note: If no working shown, award N2 for one correct value.

[3 marks]

c.i.

correct working (A1)

eg $\frac{{2\pi }}{b}$

1.04719

$\frac{{2\pi }}{6}\,\,\,\left( { = \frac{\pi }{3}} \right)$ , 1.05 A1 N2

[2 marks]

c.ii.

valid approach (M1)

eg , ${\text{si}}{{\text{n}}^{ - 1}}\left( { - \frac{8}{{10}}} \right){\text{, }}6x = - 0.927{\text{, }} - 0.154549{\text{, }}x = 0.678147$

Note: Award M1 for any correct value for $x$ or $6x$ which lies outside the domain of $f$ .

3.81974, 4.03424

$x = 3.82$ , $x = 4.03$ (do not accept answers in degrees) A1A1 N3

[3 marks]

Examiners report

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

The graph of the quadratic function $f (x) = \frac{1}{2} (x - 2) (x + 8)$ intersects the $y$ -axis at $(0, c)$ .

The vertex of the function is $(- 3, - 12.5)$ .

The equation $f (x) = 12$ has two solutions. The first solution is $x = - 10$ .

Let $T$ be the tangent at $x = - 3$ .

Find the value of $c$ .

[2]

Write down the equation for the axis of symmetry of the graph.

[2]

Use the symmetry of the graph to show that the second solution is $x = 4$ .

[1]

Write down the $x$ -intercepts of the graph.

[2]

On graph paper, draw the graph of $y = f (x)$ for $- 10 \leq x \leq 4$ and $- 14 \leq y \leq 14$ . Use a scale of $1 cm$ to represent $1$ unit on the $x$ -axis and $1 cm$ to represent $2$ units on the $y$ -axis.

[4]

Write down the equation of $T$ .

[2]

f.i.

Draw the tangent $T$ on your graph.

[1]

f.ii.

Given $f (a) = 5.5$ and $f' (a) = - 6$ , state whether the function, $f$ , is increasing or decreasing at $x = a$ . Give a reason for your answer.

[2]

Markscheme

$\frac{1}{2} (0 - 2) (0 + 8)$ OR $\frac{1}{2} (0^{2} + 6 (0) - 16)$ (or equivalent) (M1)

Note: Award (M1) for evaluating $f (0)$ .

$(c =) - 8$ (A1)(G2)

Note: Award (G2) if $- 8$ or $(0, - 8)$ seen.

[2 marks]

$x = - 3$ (A1)(A1)

Note: Award (A1) for “ $x =$ constant”, (A1) for the constant being $- 3$ . The answer must be an equation.

[2 marks]

$(- 3 - - 10) + - 3$ (M1)

$(- 8 - - 10) + 2$ (M1)

$\frac{- 10 + x}{2} = - 3$ (M1)

diagram showing axis of symmetry and given points ( $x$ -values labels, $- 10$ , $- 3$ and $4$ , are sufficient) and an indication that the horizontal distances between the axis of symmetry and the given points are $7$ . (M1)

Note: Award (M1) for correct working using the symmetry between $x = - 10$ and $x = - 3$ . Award (M0) if candidate has used $x = - 10$ and $x = 4$ to show the axis of symmetry is $x = - 3$ . Award (M0) if candidate solved $f (x) = 12$ or evaluated $f (- 10)$ and $f (4)$ .

$(x =) 4$ (AG)

[1 mark]

$- 8$ and $2$ (A1)(A1)

Note: Accept $x = - 8, y = 0$ and $x = 2, y = 0$ or $(- 8, 0)$ and $(2, 0)$ , award at most (A0)(A1) if parentheses are omitted.

[2 marks]

(A1)(A1)(A1)(A1)(ft)

Note: Award (A1) for labelled axes with correct scale, correct window. Award (A1) for the vertex, $(- 3, - 12.5)$ , in correct location.
Award (A1) for a smooth continuous curve symmetric about their vertex. Award (A1)(ft) for the curve passing through their $x$ and $y$ intercepts in correct location. Follow through from their parts (a) and (d).

If graph paper is not used:
Award at most (A0)(A0)(A1)(A1)(ft). Their graph should go through their $- 8$ and $2$ for the last (A1)(ft) to be awarded.

[4 marks]

$y = - 12.5$ OR $y = 0 x - 12.5$ (A1)(A1)

Note: Award (A1) for " $y =$ constant", (A1) for the constant being $- 12.5$ . The answer must be an equation.

[2 marks]

f.i.

tangent to the graph drawn at $x = - 3$ (A1)(ft)

Note: Award (A1) for a horizontal straight-line tangent to curve at approximately $x = - 3$ . Award (A0) if a ruler is not used. Follow through from their part (e).

[1 mark]

f.ii.

decreasing (A1)

gradient (of tangent line) is negative (at $x = a$ ) OR $f' (a) < 0$ (R1)

Note: Do not accept "gradient (of tangent line) is $- 6$ ". Do not award (A1)(R0).

[2 marks]

Examiners report

[N/A]

f.i.

[N/A]

f.ii.

[N/A]

The diagram below shows a circular clockface with centre $O$ . The clock’s minute hand has a length of $10 cm$ . The clock’s hour hand has a length of $6 cm$ .

At $4 : 00$ pm the endpoint of the minute hand is at point $A$ and the endpoint of the hour hand is at point $B$ .

Between $4 : 00$ pm and $4 : 13$ pm, the endpoint of the minute hand rotates through an angle, $θ$ , from point $A$ to point $C$ . This is illustrated in the diagram.

A second clock is illustrated in the diagram below. The clock face has radius $10 cm$ with minute and hour hands both of length $10 cm$ . The time shown is $6 : 00$ am. The bottom of the clock face is located $3 cm$ above a horizontal bookshelf.

The height, $h$ centimetres, of the endpoint of the minute hand above the bookshelf is modelled by the function

$h (θ) = 10 \cos θ + 13, θ \geq 0,$

where $θ$ is the angle rotated by the minute hand from $6 : 00$ am.

The height, $g$ centimetres, of the endpoint of the hour hand above the bookshelf is modelled by the function

$g (θ) = - 10 \cos (\frac{θ}{12}) + 13, θ \geq 0,$

where $θ$ is the angle in degrees rotated by the minute hand from $6 : 00$ am.

Find the size of angle $A \hat{O} B$ in degrees.

[2]

Find the distance between points $A$ and $B$ .

[3]

Find the size of angle $θ$ in degrees.

[2]

Calculate the length of arc $AC$ .

[2]

Calculate the area of the shaded sector, $AOC$ .

[2]

Write down the height of the endpoint of the minute hand above the bookshelf at $6 : 00$ am.

[1]

Find the value of $h$ when $θ = 160 °$ .

[2]

Write down the amplitude of $g (θ)$ .

[1]

The endpoints of the minute hand and hour hand meet when $θ = k$ .

Find the smallest possible value of $k$ .

[2]

Markscheme

$4 \times \frac{360 °}{12}$ OR $4 \times 30 °$ (M1)

$120 °$ A1

[2 marks]

substitution in cosine rule (M1)

${AB}^{2} = 10^{2} + 6^{2} - 2 \times 10 \times 6 \times \cos (120 °)$ (A1)

$AB = 14$ $cm$ A1

Note: Follow through marks in part (b) are contingent on working seen.

[3 marks]

$θ = 13 \times 6$ (M1)

$= 78 °$ A1

[2 marks]

substitution into the formula for arc length (M1)

$l = \frac{78}{360} \times 2 \times π \times 10$ OR $l = \frac{13 π}{30} \times 10$

$= 13.6 cm (13.6135 \dots, 4.33 π, \frac{13 π}{3})$ A1

[2 marks]

substitution into the area of a sector (M1)

$A = \frac{78}{360} \times π \times 10^{2}$ OR $l = \frac{1}{2} \times \frac{13 π}{30} \times 10^{2}$

$= 68.1 {cm}^{2} (68.0678 \dots, 21.7 π, \frac{65 π}{3})$ A1

[2 marks]

$23$ A1

[1 mark]

correct substitution (M1)

$h = 10 \cos (160 °) + 13$

$= 3.60 cm (3.60307 \dots)$ A1

[2 marks]

$10$ A1

[1 mark]

EITHER

$10 \times \cos (θ) + 13 = - 10 \times \cos (\frac{θ}{12}) + 13$ (M1)

(M1)

Note: Award M1 for equating the functions. Accept a sketch of $h (θ)$ and $g (θ)$ with point(s) of intersection marked.

THEN

$k = 196 ° (196.363 \dots)$ A1

Note: The answer $166.153 \dots$ is incorrect but the correct method is implicit. Award (M1)A0.

[2 marks]

Examiners report

[N/A]

Boris recorded the number of daylight hours on the first day of each month in a northern hemisphere town.

This data was plotted onto a scatter diagram. The points were then joined by a smooth curve, with minimum point $(0, 8)$ and maximum point $(6, 16)$ as shown in the following diagram.

Let the curve in the diagram be $y = f (t)$ , where $t$ is the time, measured in months, since Boris first recorded these values.

Boris thinks that $f (t)$ might be modelled by a quadratic function.

Paula thinks that a better model is $f (t) = a \cos (b t) + d$ , $t \geq 0$ , for specific values of $a, b$ and $d$ .

For Paula’s model, use the diagram to write down

The true maximum number of daylight hours was $16$ hours and $14$ minutes.

Write down one reason why a quadratic function would not be a good model for the number of hours of daylight per day, across a number of years.

[1]

the amplitude.

[1]

b.i.

the period.

[1]

b.ii.

the equation of the principal axis.

[2]

b.iii.

Hence or otherwise find the equation of this model in the form:

$f (t) = a \cos (b t) + d$

[3]

For the first year of the model, find the length of time when there are more than $10$ hours and $30$ minutes of daylight per day.

[4]

Calculate the percentage error in the maximum number of daylight hours Boris recorded in the diagram.

[3]

Markscheme

EITHER
annual cycle for daylight length R1

OR
there is a minimum length for daylight (cannot be negative) R1

OR
a quadratic could not have a maximum and a minimum or equivalent R1

Note: Do not accept “Paula's model is better”.

[1 mark]

$4$ A1

[1 mark]

b.i.

$12$ A1

[1 mark]

b.ii.

$y = 12$ A1A1

Note: Award A1 “ $y =$ (a constant)” and A1 for that constant being $12$ .

[2 marks]

b.iii.

$f (t) = - 4 \cos (30 t) + 12$ OR $f (t) = - 4 \cos (- 30 t) + 12$ A1A1A1

Note: Award A1 for $b = 30$ (or $b = - 30$ ), A1 for $a = - 4$ , and A1 for $d = 12$ . Award at most A1A1A0 if extra terms are seen or form is incorrect. Award at most A1A1A0 if $x$ is used instead of $t$ .

[3 marks]

$10.5 = - 4 \cos (30 t) + 12$ (M1)

EITHER

$t_{1} = 2.26585 \dots, t_{2} = 9.73414 \dots$ (A1)(A1)

$t_{1} = \frac{1}{30} \cos^{- 1} \frac{3}{8}$ (A1)

$t_{2} = 12 - t_{1}$ (A1)

THEN

$9.73414 \dots - 2.26585 \dots$

$7.47 (7.46828 \dots)$ months ( $0.622356 \dots$ years) A1

Note: Award M1A1A1A0 for an unsupported answer of $7.46$ . If there is only one intersection point, award M1A1A0A0.

[4 marks]

$|\frac{16 - (16 + \frac{14}{60})}{16 + \frac{14}{60}}| \times 100 %$ (M1)(M1)

Note: Award M1 for correct values and absolute value signs, M1 for $\times 100$ .

$= 1.44 % (1.43737 \dots %)$ A1

[3 marks]

Examiners report

Part (a) indicated a lack of understanding of quadratic functions and the cyclical nature of daylight hours. Some candidates seemed to understand the limitations of a quadratic model but were not always able to use appropriate mathematical language to explain the limitations clearly.

In part (b), many candidates struggled to write down the amplitude, period, and equation of the principal axis.

In part (c), very few candidates recognized that it would be a negative cosine graph here and most did not know how to find the “b” value even if they had originally found the period in part (b). Some candidates used the regression features in their GDC to find the equation of the model; this is outside the SL syllabus but is a valid approach and earned full credit.

In part (d), very few candidates were awarded “follow through” marks in this part. Some substituted 10.5 into their equation rather that equate their equation to 10.5 and attempt to solve it using their GDC to graph the equations or using the “solver” function.

Part (e) was perhaps the best answered part in this question. However, due to premature rounding, many candidates did not gain full marks. A common error was to write the true number of daylight hours as 16.14.

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

b.iii.

[N/A]

The rate of change of the height $(h)$ of a ball above horizontal ground, measured in metres, $t$ seconds after it has been thrown and until it hits the ground, can be modelled by the equation

$\frac{d h}{d t} = 11.4 - 9.8 t$

The height of the ball when $t = 0$ is $1.2 m$ .

Find an expression for the height $h$ of the ball at time $t$ .

[6]

Find the value of $t$ at which the ball hits the ground.

[2]

b.i.

Hence write down the domain of $h$ .

[1]

b.ii.

Find the range of $h$ .

[3]

Markscheme

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

$h = \int (11.4 - 9.8 t) d t$ M1

$h = 11.4 t - 4.9 t^{2} (+ c)$ A1A1

When $t = 0, h = 1.2$ (M1)

$c = 1.2$ (A1)

$(h =) 1.2 + 11.4 t - 4.9 t^{2}$ A1

[6 marks]

$2.43 (2.42741 \dots)$ seconds (M1)A1

[2 marks]

b.i.

$0 \leq t \leq 2.43$ A1

Note: Accept $0 \leq t < 2.43$ .

[1 mark]

b.ii.

Maximum value is $7.83061 \dots$ (M1)

Range is $0 \leq h \leq 7.83$ A1A1

Note: Accept $0 \leq h < 7.83$ .

[3 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

In the month before their IB Diploma examinations, eight male students recorded the number of hours they spent on social media.

For each student, the number of hours spent on social media ( $x$ ) and the number of IB Diploma points obtained ( $y$ ) are shown in the following table.

N16/5/MATSD/SP2/ENG/TZ0/01

Use your graphic display calculator to find

Ten female students also recorded the number of hours they spent on social media in the month before their IB Diploma examinations. Each of these female students spent between 3 and 30 hours on social media.

The equation of the regression line y on x for these ten female students is

$y = - \frac{2}{3}x + \frac{{125}}{3}.$

An eleventh girl spent 34 hours on social media in the month before her IB Diploma examinations.

On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the $x$ -axis and 2 cm to represent 10 points on the $y$ -axis.

[4]

(i) ${\bar x}$ , the mean number of hours spent on social media;

(ii) ${\bar y}$ , the mean number of IB Diploma points.

[2]

Plot the point $(\bar x,{\text{ }}\bar y)$ on your scatter diagram and label this point M.

[2]

Write down the equation of the regression line $y$ on $x$ for these eight male students.

[2]

Draw the regression line, from part (e), on your scatter diagram.

[2]

Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.

[2]

Write down a reason why this estimate is not reliable.

[1]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

N16/5/MATSD/SP2/ENG/TZ0/01.a/M (A4)

Notes: Award (A1) for correct scale and labelled axes.

Award (A3) for 7 or 8 points correctly plotted,

(A2) for 5 or 6 points correctly plotted,

(A1) for 3 or 4 points correctly plotted.

Award at most (A0)(A3) if axes reversed.

Accept $x$ and $y$ sufficient for labelling.

If graph paper is not used, award (A0).

If an inconsistent scale is used, award (A0). Candidates’ points should be read from this scale where possible and awarded accordingly.

A scale which is too small to be meaningful (ie mm instead of cm) earns (A0) for plotted points.

[4 marks]

(i) $\bar x = 21$ (A1)

(ii) $\bar y = 31$ (A1)

[2 marks]

$(\bar x,{\text{ }}\bar y)$ correctly plotted on graph (A1)(ft)

this point labelled M (A1)

Note: Follow through from parts (b)(i) and (b)(ii).

Only accept M for labelling.

[2 marks]

$y = - 0.761x + 47.0{\text{ }}(y = - 0.760638 \ldots x + 46.9734 \ldots )$ (A1)(A1)(G2)

Notes: Award (A1) for $- 0.761x$ and (A1) $+ 47.0$ . Award a maximum of (A1)(A0) if answer is not an equation.

[2 marks]

line on graph (A1)(ft)(A1)(ft)

Notes: Award (A1)(ft) for straight line that passes through their M, (A1)(ft) for line (extrapolated if necessary) that passes through $(0,{\text{ }}47.0)$ .

If M is not plotted or labelled, follow through from part (e).

[2 marks]

$y = - \frac{2}{3}(34) + \frac{{125}}{3}$ (M1)

Note: Award (M1) for correct substitution.

19 (points) (A1)(G2)

[2 marks]

extrapolation (R1)

34 hours is outside the given range of data (R1)

Note: Do not accept ‘outlier’.

[1 mark]

Examiners report

[N/A]

The braking distance of a vehicle is defined as the distance travelled from where the brakes are applied to the point where the vehicle comes to a complete stop.

The speed, $s\,{\text{m}}\,{{\text{s}}^{ - 1}}$ , and braking distance, $d\,{\text{m}}$ , of a truck were recorded. This information is summarized in the following table.

This information was used to create Model A, where $d$ is a function of $s$ , $s$ ≥ 0.

Model A: $d\left( s \right) = p{s^2} + qs$ , where $p$ , $q \in \mathbb{Z}$

At a speed of $6\,{\text{m}}\,{{\text{s}}^{ - 1}}$ , Model A can be represented by the equation $6p + q = 2$ .

Additional data was used to create Model B, a revised model for the braking distance of a truck.

Model B: $d\left( s \right) = 0.95{s^2} - 3.92s$

The actual braking distance at $20\,{\text{m}}\,{{\text{s}}^{ - 1}}$ is $320\,{\text{m}}$ .

Write down a second equation to represent Model A, when the speed is $10\,{\text{m}}\,{{\text{s}}^{ - 1}}$ .

[2]

a.i.

Find the values of $p$ and $q$ .

[2]

a.ii.

Find the coordinates of the vertex of the graph of $y = d\left( s \right)$ .

[2]

Using the values in the table and your answer to part (b), sketch the graph of $y = d\left( s \right)$ for 0 ≤ $s$ ≤ 10 and −10 ≤ $d$ ≤ 60, clearly showing the vertex.

[3]

Hence, identify why Model A may not be appropriate at lower speeds.

[1]

Use Model B to calculate an estimate for the braking distance at a speed of $20\,{\text{m}}\,{{\text{s}}^{ - 1}}$ .

[2]

Calculate the percentage error in the estimate in part (e).

[2]

It is found that once a driver realizes the need to stop their vehicle, 1.6 seconds will elapse, on average, before the brakes are engaged. During this reaction time, the vehicle will continue to travel at its original speed.

A truck approaches an intersection with speed $s\,{\text{m}}\,{{\text{s}}^{ - 1}}$ . The driver notices the intersection’s traffic lights are red and they must stop the vehicle within a distance of $330\,{\text{m}}$ .

Using model B and taking reaction time into account, calculate the maximum possible speed of the truck if it is to stop before the intersection.

[3]

Markscheme

$p{\left( {10} \right)^2} + q\left( {10} \right) = 60$ M1

$10p + q = 6\left( {100p + 10q = 60} \right)$ A1

[2 marks]

a.i.

$p = 1$ , $q = - 4$ A1A1

Note: If $p$ and $q$ are both incorrect then award M1A0 for an attempt to solve simultaneous equations.

[2 marks]

a.ii.

(2, −4) A1A1

Note: Award A1 for each correct coordinate.
Award A0A1 if parentheses are missing.

[2 marks]

Note: Award A1 for smooth quadratic curve on labelled axes and within correct window.
Award A1 for the curve passing through (0, 0) and (10, 60). Award A1 for the curve passing through their vertex. Follow through from part (b).

[3 marks]

the graph indicates there are negative stopping distances (for low speeds) R1

Note: Award R1 for identifying that a feature of their graph results in negative stopping distances (vertex, range of stopping distances…).

[1 mark]

$0.95 \times {20^2} - 3.92 \times 20$ (M1)

$= 302\,\left( {\text{m}} \right)\,\,\left( {301.6 \ldots } \right)$ A1

[2 marks]

$\left| {\frac{{301.6 - 320}}{{320}}} \right| \times 100$ M1

$= 5.75$ (%) A1

[2 marks]

$330 = 1.6 \times s + 0.95 \times {s^2} - 3.92 \times s$ M1A1

Note: Award M1 for an attempt to find an expression including stopping distance (model B) and reaction distance, equated to 330. Award A1 for a completely correct equation.

$19.9\left( {{\text{m}}\,{{\text{s}}^{ - 1}}} \right)\,\,\left( {19.8988 \ldots } \right)$ A1

[3 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

Consider the function $f\left( x \right) = \frac{{48}}{x} + k{x^2} - 58$ , where x > 0 and k is a constant.

The graph of the function passes through the point with coordinates (4 , 2).

P is the minimum point of the graph of f (x).

Find the value of k.

[2]

Using your value of k , find f ′(x).

[3]

Use your answer to part (b) to show that the minimum value of f(x) is −22 .

[3]

Sketch the graph of y = f (x) for 0 < x ≤ 6 and −30 ≤ y ≤ 60.
Clearly indicate the minimum point P and the x-intercepts on your graph.

[4]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{{48}}{4} + k \times {4^2} - 58 = 2$ (M1)
Note: Award (M1) for correct substitution of x = 4 and y = 2 into the function.

k = 3 (A1) (G2)

[2 marks]

$\frac{{ - 48}}{{{x^2}}} + 6x$ (A1)(A1)(A1)(ft) (G3)

Note: Award (A1) for −48 , (A1) for x⁻², (A1)(ft) for their 6x. Follow through from part (a). Award at most (A1)(A1)(A0) if additional terms are seen.

[3 marks]

$\frac{{ - 48}}{{{x^2}}} + 6x = 0$ (M1)

Note: Award (M1) for equating their part (b) to zero.

x = 2 (A1)(ft)

Note: Follow through from part (b). Award (M1)(A1) for $\frac{{ - 48}}{{{{\left( 2 \right)}^2}}} + 6\left( 2 \right) = 0$ seen.

Award (M0)(A0) for x = 2 seen either from a graphical method or without working.

$\frac{{48}}{2} + 3 \times {2^2} - 58\,\,\,\left( { = - 22} \right)$ (M1)

Note: Award (M1) for substituting their 2 into their function, but only if the final answer is −22. Substitution of the known result invalidates the process; award (M0)(A0)(M0).

−22 (AG)

[3 marks]

(A1)(A1)(ft)(A1)(ft)(A1)(ft)

Note: Award (A1) for correct window. Axes must be labelled.
(A1)(ft) for a smooth curve with correct shape and zeros in approximately correct positions relative to each other.
(A1)(ft) for point P indicated in approximately the correct position. Follow through from their x-coordinate in part (c). (A1)(ft) for two x-intercepts identified on the graph and curve reflecting asymptotic properties.

[4 marks]

Examiners report

[N/A]

A cafe makes $x$ litres of coffee each morning. The cafe’s profit each morning, $C$ , measured in dollars, is modelled by the following equation

$C = \frac{x}{10} (k^{2} - \frac{3}{100} x^{2})$

where $k$ is a positive constant.

The cafe’s manager knows that the cafe makes a profit of $$ 426$ when $20$ litres of coffee are made in a morning.

The manager of the cafe wishes to serve as many customers as possible.

Find an expression for $\frac{d C}{d x}$ in terms of $k$ and $x$ .

[3]

Hence find the maximum value of $C$ in terms of $k$ . Give your answer in the form $p k^{3}$ , where $p$ is a constant.

[4]

Find the value of $k$ .

[2]

c.i.

Use the model to find how much coffee the cafe should make each morning to maximize its profit.

[1]

c.ii.

Sketch the graph of $C$ against $x$ , labelling the maximum point and the $x$ -intercepts with their coordinates.

[3]

Determine the maximum amount of coffee the cafe can make that will not result in a loss of money for the morning.

[2]

Markscheme

attempt to expand given expression (M1)

$C = \frac{x k^{2}}{10} - \frac{3 x^{3}}{1000}$

$\frac{d C}{d x} = \frac{k^{2}}{10} - \frac{9 x^{2}}{1000}$ M1A1

Note: Award M1 for power rule correctly applied to at least one term and A1 for correct answer.

[3 marks]

equating their $\frac{d C}{d x}$ to zero (M1)

$\frac{k^{2}}{10} - \frac{9 x^{2}}{1000} = 0$

$x^{2} = \frac{100 k^{2}}{9}$

$x = \frac{10 k}{3}$ (A1)

substituting their $x$ back into given expression (M1)

$C_{max} = \frac{10 k}{30} (k^{2} - \frac{300 k^{2}}{900})$

$C_{max} = \frac{2 k^{3}}{9} (0.222 \dots k^{3})$ A1

[4 marks]

substituting $20$ into given expression and equating to $426$ M1

$426 = \frac{20}{10} (k^{2} - \frac{3}{100} {(20)}^{2})$

$k = 15$ A1

[2 marks]

c.i.

$50$ A1

[1 mark]

c.ii.

A1A1A1

Note: Award A1 for graph drawn for positive $x$ indicating an increasing and then decreasing function, A1 for maximum labelled and A1 for graph passing through the origin and $86.6$ , marked on the $x$ -axis or whose coordinates are given.

[3 marks]

setting their expression for $C$ to zero OR choosing correct $x$ -intercept on their graph of $C$ (M1)

$x_{max} = 86.6 (86.6025 \dots)$ litres A1

[2 marks]

Examiners report

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

Let $f\left( x \right) = \frac{{16}}{x}$ . The line $L$ is tangent to the graph of $f$ at $x = 8$ .

$L$ can be expressed in the form r $= \left( {\begin{array}{*{20}{c}} 8 \\ 2 \end{array}} \right) + t$ u.

The direction vector of $y = x$ is $\left( {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right)$ .

Find the gradient of $L$ .

[2]

Find u.

[2]

Find the acute angle between $y = x$ and $L$ .

[5]

Find $\left( {f \circ f} \right)\left( x \right)$ .

[3]

d.i.

Hence, write down ${f^{ - 1}}\left( x \right)$ .

[1]

d.ii.

Hence or otherwise, find the obtuse angle formed by the tangent line to $f$ at $x = 8$ and the tangent line to $f$ at $x = 2$ .

[3]

d.iii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to find $f'\left( 8 \right)$ (M1)

eg $f'\left( x \right)$ , ${y'}$ , $- 16{x^{ - 2}}$

−0.25 (exact) A1 N2

[2 marks]

u $= \left( {\begin{array}{*{20}{c}} 4 \\ { - 1} \end{array}} \right)$ or any scalar multiple A2 N2

[2 marks]

correct scalar product and magnitudes (A1)(A1)(A1)

scalar product $= 1 \times 4 + 1 \times - 1\,\,\,\left( { = 3} \right)$

magnitudes $= \sqrt {{1^2} + {1^2}}$ , $\sqrt {{4^2} + {{\left( { - 1} \right)}^2}}$ $\left( { = \sqrt 2 {\text{,}}\,\,\sqrt {17} } \right)$

substitution of their values into correct formula (M1)

eg $\frac{{4 - 1}}{{\sqrt {{1^2} + {1^2}} \sqrt {{4^2} + {{\left( { - 1} \right)}^2}} }}$ , $\frac{{ - 3}}{{\sqrt 2 \sqrt {17} }}$ , 2.1112, 120.96°

1.03037 , 59.0362°

angle = 1.03 , 59.0° A1 N4

[5 marks]

attempt to form composite $\left( {f \circ f} \right)\left( x \right)$ (M1)

eg $f\left( {f\left( x \right)} \right)$ , $f\left( {\frac{{16}}{x}} \right)$ , $\frac{{16}}{{f\left( x \right)}}$

correct working (A1)

eg $\frac{{16}}{{\frac{{16}}{x}}}$ , $16 \times \frac{x}{{16}}$

$\left( {f \circ f} \right)\left( x \right) = x$ A1 N2

[3 marks]

d.i.

${f^{ - 1}}\left( x \right) = \frac{{16}}{x}$ (accept $y = \frac{{16}}{x}$ , $\frac{{16}}{x}$ ) A1 N1

Note: Award A0 in part (ii) if part (i) is incorrect.
Award A0 in part (ii) if the candidate has found ${f^{ - 1}}\left( x \right) = \frac{{16}}{x}$ by interchanging $x$ and $y$ .

[1 mark]

d.ii.

METHOD 1

recognition of symmetry about $y = x$ (M1)

eg (2, 8) ⇔ (8, 2)

evidence of doubling their angle (M1)

eg $2 \times 1.03$ , $2 \times 59.0$

2.06075, 118.072°

2.06 (radians) (118 degrees) A1 N2

METHOD 2

finding direction vector for tangent line at $x = 2$ (A1)

eg $\left( {\begin{array}{*{20}{c}} { - 1} \\ 4 \end{array}} \right)$ , $\left( {\begin{array}{*{20}{c}} 1 \\ { - 4} \end{array}} \right)$

substitution of their values into correct formula (must be from vectors) (M1)

eg $\frac{{ - 4 - 4}}{{\sqrt {{1^2} + {4^2}} \sqrt {{4^2} + {{\left( { - 1} \right)}^2}} }}$ , $\frac{8}{{\sqrt {17} \sqrt {17} }}$

2.06075, 118.072°

2.06 (radians) (118 degrees) A1 N2

METHOD 3

using trigonometry to find an angle with the horizontal (M1)

eg ${\text{tan}}\,\theta = - \frac{1}{4}$ , ${\text{tan}}\,\theta = - 4$

finding both angles of rotation (A1)

eg ${\theta _1} = 0.244978{\text{, 14}}{\text{.0362}}^\circ$ , ${\theta _1} = 1.81577{\text{, 104}}{\text{.036}}^\circ$

2.06075, 118.072°

2.06 (radians) (118 degrees) A1 N2

[3 marks]

d.iii.

Examiners report

[N/A]

d.i.

[N/A]

d.ii.

[N/A]

d.iii.

The depth of water in a port is modelled by the function $d(t) = p\cos qt + 7.5$ , for $0 \leqslant t \leqslant 12$ , where $t$ is the number of hours after high tide.

At high tide, the depth is 9.7 metres.

At low tide, which is 7 hours later, the depth is 5.3 metres.

Find the value of $p$ .

[2]

Find the value of $q$ .

[2]

Use the model to find the depth of the water 10 hours after high tide.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

valid approach (M1)

eg $\,\,\,\,\,$ $\frac{{{\text{max}} - {\text{min}}}}{2}$ , sketch of graph, $9.7 = p\cos (0) + 7.5$

$p = 2.2$ A1 N2

[2 marks]

valid approach (M1)

eg $\,\,\,\,\,$ $B = \frac{{2\pi }}{{{\text{period}}}}$ , period is $14,{\text{ }}\frac{{360}}{{14}},{\text{ }}5.3 = 2.2\cos 7q + 7.5$

0.448798

$q = \frac{{2\pi }}{{14}}{\text{ }}\left( {\frac{\pi }{7}} \right)$ , (do not accept degrees) A1 N2

[2 marks]

valid approach (M1)

eg $\,\,\,\,\,$ $d(10),{\text{ }}2.2\cos \left( {\frac{{20\pi }}{{14}}} \right) + 7.5$

7.01045

7.01 (m) A1 N2

[2 marks]

Examiners report

[N/A]

Consider the function $f(x) = - {x^4} + a{x^2} + 5$ , where $a$ is a constant. Part of the graph of $y = f(x)$ is shown below.

M17/5/MATSD/SP2/ENG/TZ2/06

It is known that at the point where $x = 2$ the tangent to the graph of $y = f(x)$ is horizontal.

There are two other points on the graph of $y = f(x)$ at which the tangent is horizontal.

Write down the $y$ -intercept of the graph.

[1]

Find $f'(x)$ .

[2]

Show that $a = 8$ .

[2]

c.i.

Find $f(2)$ .

[2]

c.ii.

Write down the $x$ -coordinates of these two points;

[2]

d.i.

Write down the intervals where the gradient of the graph of $y = f(x)$ is positive.

[2]

d.ii.

Write down the range of $f(x)$ .

[2]

Write down the number of possible solutions to the equation $f(x) = 5$ .

[1]

The equation $f(x) = m$ , where $m \in \mathbb{R}$ , has four solutions. Find the possible values of $m$ .

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

5 (A1)

Note: Accept an answer of $(0,{\text{ }}5)$ .

[1 mark]

$\left( {f'(x) = } \right) - 4{x^3} + 2ax$ (A1)(A1)

Note: Award (A1) for $- 4{x^3}$ and (A1) for $+ 2ax$ . Award at most (A1)(A0) if extra terms are seen.

[2 marks]

$- 4 \times {2^3} + 2a \times 2 = 0$ (M1)(M1)

Note: Award (M1) for substitution of $x = 2$ into their derivative, (M1) for equating their derivative, written in terms of $a$ , to 0 leading to a correct answer (note, the 8 does not need to be seen).

$a = 8$ (AG)

[2 marks]

c.i.

$\left( {f(2) = } \right) - {2^4} + 8 \times {2^2} + 5$ (M1)

Note: Award (M1) for correct substitution of $x = 2$ and $a = 8$ into the formula of the function.

21 (A1)(G2)

[2 marks]

c.ii.

$(x = ){\text{ }} - 2,{\text{ }}(x = ){\text{ 0}}$ (A1)(A1)

Note: Award (A1) for each correct solution. Award at most (A0)(A1)(ft) if answers are given as $( - 2{\text{ }},21)$ and $(0,{\text{ }}5)$ or $( - 2,{\text{ }}0)$ and $(0,{\text{ }}0)$ .

[2 marks]

d.i.

$x < - 2,{\text{ }}0 < x < 2$ (A1)(ft)(A1)(ft)

Note: Award (A1)(ft) for $x < - 2$ , follow through from part (d)(i) provided their value is negative.

Award (A1)(ft) for $0 < x < 2$ , follow through only from their 0 from part (d)(i); 2 must be the upper limit.

Accept interval notation.

[2 marks]

d.ii.

$y \leqslant 21$ (A1)(ft)(A1)

Notes: Award (A1)(ft) for 21 seen in an interval or an inequality, (A1) for “ $y \leqslant$ ”.

Accept interval notation.

Accept $- \infty < y \leqslant 21$ or $f(x) \leqslant 21$ .

Follow through from their answer to part (c)(ii). Award at most (A1)(ft)(A0) if $x$ is seen instead of $y$ . Do not award the second (A1) if a (finite) lower limit is seen.

[2 marks]

3 (solutions) (A1)

[1 mark]

$5 < m < 21$ or equivalent (A1)(ft)(A1)

Note: Award (A1)(ft) for 5 and 21 seen in an interval or an inequality, (A1) for correct strict inequalities. Follow through from their answers to parts (a) and (c)(ii).

Accept interval notation.

[2 marks]

Examiners report

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

d.i.

[N/A]

d.ii.

[N/A]

Let $f(x) = {x^2} + 2x + 1$ and $g(x) = x - 5$ , for $x \in \mathbb{R}$ .

Find $f(8)$ .

[2]

Find $(g \circ f)(x)$ .

[2]

Solve $(g \circ f)(x) = 0$ .

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to substitute $x = 8$ (M1)

eg $\,\,\,\,\,$ ${8^2} + 2 \times 8 + 1$

$f(8) = 81$ A1 N2

[2 marks]

attempt to form composition (in any order) (M1)

eg $\,\,\,\,\,$ $f(x - 5),{\text{ }}g\left( {f(x)} \right),{\text{ }}\left( {{x^2} + 2x + 1} \right) - 5$

$(g \circ f)(x) = {x^2} + 2x - 4$ A1 N2

[2 marks]

valid approach (M1)

eg $x = \frac{{ - 2 \pm \sqrt {20} }}{2}$ , N16/5/MATME/SP2/ENG/TZ0/01.c/M

$1.23606,{\text{ }} - 3.23606$

$x = 1.24,{\text{ }}x = - 3.24$ A1A1 N3

[3 marks]

Examiners report

[N/A]

Consider the function $f (x) = x^{2} + x + \frac{50}{x}, x \neq 0 .$

Find $f (1)$ .

[2]

Solve $f (x) = 0$ .

[2]

The graph of $f$ has a local minimum at point $A$ .

Find the coordinates of $A$ .

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to substitute $x = 1$ (M1)

eg $f (1), 1^{2} + 1 + \frac{50}{1}$

$52$ (exact) A1 N2

[2 marks]

$- 4.04932$

$- 4.05$ A2 N2

[2 marks]

$(2.76649, 28.4934)$

$A (2.77, 28.5)$ A1A1 N2

[2 marks]

Examiners report

[N/A]

The following diagram shows a water wheel with centre $O$ and radius $10$ metres. Water flows into buckets, turning the wheel clockwise at a constant speed.

The height, $h$ metres, of the top of a bucket above the ground $t$ seconds after it passes through point $A$ is modelled by the function

$h (t) = 13 + 8 \cos (\frac{π}{18} t) - 6 \sin (\frac{π}{18} t)$ , for $t \geq 0$ .

A bucket moves around to point $B$ which is at a height of $4.06$ metres above the ground. It takes $k$ seconds for the top of this bucket to go from point $A$ to point $B$ .

The chord $[AB]$ is $17.0$ metres, correct to three significant figures.

Find the height of point $A$ above the ground.

[2]

a.i.

Calculate the number of seconds it takes for the water wheel to complete one rotation.

[2]

a.ii.

Hence find the number of rotations the water wheel makes in one hour.

[2]

a.iii.

Find $k$ .

[3]

Find $A \hat{O} B$ .

[3]

Determine the rate of change of $h$ when the top of the bucket is at $B$ .

[2]

Markscheme

valid approach (M1)

eg $h (0), 13 + 8 \cos (\frac{π}{18} \times 0) - 6 \sin (\frac{π}{18} \times 0), 13 + 8 \times 1 - 6 \times 0$

$21$ (metres) A1 N2

[2 marks]

a.i.

valid approach to find the period (seen anywhere) (M1)

eg $(36, 21)$ , attempt to find two consecutive max/min, $50.3130 - 14.3130$

$\frac{2 π}{\frac{π}{18}}, b = \frac{2 π}{period},$

$36$ (seconds) (exact) A1 N2

[2 marks]

a.ii.

correct approach (A1)

eg $\frac{60 \times 60}{36}, 1.6666$ rotations per minute

$100$ (rotations) A1 N2

[2 marks]

a.iii.

correct substitution into equation (accept the use of $t$ ) (A1)

eg $4.06 = 13 + 8 \cos (\frac{π}{18} \times k) - 6 \sin (\frac{π}{18} \times k)$

valid attempt to solve their equation (M1)

$11.6510$

$11.7$ A1 N3

[3 marks]

METHOD 1

evidence of choosing the cosine rule or sine rule (M1)

eg ${AB}^{2} = {OA}^{2} + {OB}^{2} - 2 \times OA \times OB \cos (A \hat{O} B), \frac{\sin (A \hat{O} B)}{AB} = \frac{\sin (O \hat{A} B)}{OB}$

correct working (A1)

eg $\cos (A \hat{O} B) = \frac{10^{2} + 10^{2} - 17 . 0^{2}}{2 \times 10 \times 10}, - 0.445, \frac{\sin (A \hat{O} B)}{17.0} = \frac{\sin (\frac{π}{2} - \frac{1}{2} A \hat{O} B)}{10},$

$\frac{\sin (O \hat{A} B)}{10} = \frac{\sin (π - 2 \times O \hat{A} B)}{17.0}$

$2.03197, 116.423 °$

$2.03 (116 °)$ A1 N3

METHOD 2

attempt to find the half central angle (M1)

eg $\sin (\frac{1}{2} A \hat{O} B) = \frac{\frac{1}{2} AB}{OA}$

correct working (A1)

eg $2 \times \sin^{- 1} (\frac{8.5}{10})$

$2.03197, 116.423 °$

$2.03 (116 °)$ A1 N3

METHOD 3

valid approach to find fraction of period (M1)

eg $\frac{k}{36}, \frac{11.6510}{36}$

correct approach to find angle (A1)

eg $\frac{k}{36} \times 2 π$

$2.03348, 116.510 °$ ( $2.04203$ using $11.7$ )

$2.03 (117 °)$ A1 N3

[3 marks]

recognizing rate of change is $h'$ (M1)

eg $h' (k), h' (11.6510), 0.782024$

$- 0.782024$ ( $- 0.768662$ from $3 sf$ )

rate of change is $- 0.782 ({ms}^{- 1})$ A1 N2

( $- 0.769 ({ms}^{- 1})$ from $3 sf$ )

[2 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

a.iii.

[N/A]

Scott purchases food for his dog in large bags and feeds the dog the same amount of dog food each day. The amount of dog food left in the bag at the end of each day can be modelled by an arithmetic sequence.

On a particular day, Scott opened a new bag of dog food and fed his dog. By the end of the third day there were $115.5$ cups of dog food remaining in the bag and at the end of the eighth day there were $108$ cups of dog food remaining in the bag.

Find the number of cups of dog food

In $2021$ , Scott spent $$ 625$ on dog food. Scott expects that the amount he spends on dog food will increase at an annual rate of $6.4 %$ .

fed to the dog per day.

[3]

a.i.

remaining in the bag at the end of the first day.

[1]

a.ii.

Calculate the number of days that Scott can feed his dog with one bag of food.

[2]

Determine the amount that Scott expects to spend on dog food in $2025$ . Round your answer to the nearest dollar.

[3]

Calculate the value of $Σ_{n = 1}^{10} (625 \times 1 . 064^{(n - 1)})$ .

[1]

d.i.

Describe what the value in part (d)(i) represents in this context.

[2]

d.ii.

Comment on the appropriateness of modelling this scenario with a geometric sequence.

[1]

Markscheme

EITHER

$115.5 = u_{1} + (3 - 1) \times d (115.5 = u_{1} + 2 d)$

$108 = u_{1} + (8 - 1) \times d (108 = u_{1} + 7 d)$ (M1)(A1)

Note: Award M1 for attempting to use the arithmetic sequence term formula, A1 for both equations correct. Working for M1 and A1 can be found in parts (i) or (ii).

$(d = - 1.5)$

$1.5$ (cups/day) A1

Note: Answer must be written as a positive value to award A1.

$(d =) \frac{115.5 - 108}{5}$ (M1)(A1)

Note: Award M1 for attempting a calculation using the difference between term $3$ and term $8$ ; A1 for a correct substitution.

$(d =) 1.5$ (cups/day) A1

[3 marks]

a.i.

$(u_{1} =) 118.5$ (cups) A1

[1 mark]

a.ii.

attempting to substitute their values into the term formula for arithmetic sequence equated to zero (M1)

$0 = 118.5 + (n - 1) \times (- 1.5)$

$(n =) 80$ days A1

Note: Follow through from part (a) only if their answer is positive.

[2 marks]

$(t_{5} =) 625 \times 1 . 064^{(5 - 1)}$ (M1)(A1)

Note: Award M1 for attempting to use the geometric sequence term formula; A1 for a correct substitution

$$ 801$ A1

Note: The answer must be rounded to a whole number to award the final A1.

[3 marks]

$(S_{10} =) ($) 8390 (8394.39 \dots)$ A1

[1 mark]

d.i.

EITHER

the total cost (of dog food) R1

for $10$ years beginning in $2021$ OR $10$ years before $2031$ R1

the total cost (of dog food) R1

from $2021$ to $2030$ (inclusive) OR from $2021$ to (the start of) $2031$ R1

[2 marks]

d.ii.

EITHER
According to the model, the cost of dog food per year will eventually be too high to keep a dog.

OR
The model does not necessarily consider changes in inflation rate.

OR
The model is appropriate as long as inflation increases at a similar rate.

OR
The model does not account for changes in the amount of food the dog eats as it ages/becomes ill/stops growing.

OR
The model is appropriate since dog food bags can only be bought in discrete quantities. R1

Note: Accept reasonable answers commenting on the appropriateness of the model for the specific scenario. There should be a reference to the given context. A reference to the geometric model must be clear: either “model” is mentioned specifically, or other mathematical terms such as “increasing” or “discrete quantities” are seen. Do not accept a contextual argument in isolation, e.g. “The dog will eventually die”.

[1 mark]

Examiners report

Parts (a) and (b) were mostly well answered, but some candidates ignored the context and did not give the number of dog food cups per day as a positive number. Most candidates considered geometric sequence in part (c) correctly, and used the correct formula for the nth term, although they used an incorrect value for n at times. Some candidates used the finance application incorrectly. The sum in part (d) was calculated correctly by some candidates, although many seemed unfamiliar with sigma notation and with calculating summations using GDC. In part (d), most candidates interpreted correctly that the sum represented the cost of dog food for 10 years but did not identify the specific 10-year period. Part (e) was not answered well – often candidates made very general and abstract statements devoid of any contextual references.

a.i.

[N/A]

a.ii.

[N/A]

d.i.

[N/A]

d.ii.

[N/A]

Consider the function $f\left( x \right) = {x^3} - 5{x^2} + 6x - 3 + \frac{1}{x}$ , $x > 0$

The function $f\left( x \right) = {x^3} - 5{x^2} + 6x - 3 + \frac{1}{x}$ , $x > 0$ , models the path of a river, as shown on the following map, where both axes represent distance and are measured in kilometres. On the same map, the location of a highway is defined by the function $g\left( x \right) = 0.5{\left( 3 \right)^{ - x}} + 1$ .

The origin, O(0, 0) , is the location of the centre of a town called Orangeton.

A straight footpath, $P$ , is built to connect the centre of Orangeton to the river at the point where $x = \frac{1}{2}$ .

Bridges are located where the highway crosses the river.

A straight road is built from the centre of Orangeton, due north, to connect the town to the highway.

State the domain of $P$ .

[2]

b.ii.

Find the distance from the centre of Orangeton to the point at which the road meets the highway.

[2]

This straight road crosses the highway and then carries on due north.

State whether the straight road will ever cross the river. Justify your answer.

[2]

Markscheme

0 < $x$ < $\frac{1}{2}$ (A1)(A1)

Note: Award (A1) for both endpoints correct, (A1) for correct mathematical notation indicating an interval with two endpoints. Accept weak inequalities. Award at most (A1)(A0) for incorrect notation such as 0 − 0.5 or a written description of the domain with correct endpoints. Award at most (A1)(A0) for 0 < $y$ < $\frac{1}{2}$ .

[2 marks]

b.ii.

$g\left( 0 \right) = 0.5{\left( 3 \right)^0} + 1$ (M1)

1.5 (km) (A1)(G2)

[2 marks]

domain given as $x > 0$ (but equation of road is $x = 0$ ) (R1)

(equation of road is $x = 0$ ) the function of the river is asymptotic to $x = 0$ (R1)

so it does not meet the river (A1)

Note: Award the (R1) for a correct mathematical statement about the equation of the river (and the equation of the road). Justification must be based on mathematical reasoning. Do not award (R0)(A1).

[2 marks]

Examiners report

[N/A]

b.ii.

[N/A]

Note: In this question, distance is in millimetres.

Let $f(x) = x + a\sin \left( {x - \frac{\pi }{2}} \right) + a$ , for $x \geqslant 0$ .

The graph of $f$ passes through the origin. Let ${{\text{P}}_k}$ be any point on the graph of $f$ with $x$ -coordinate $2k\pi$ , where $k \in \mathbb{N}$ . A straight line $L$ passes through all the points ${{\text{P}}_k}$ .

Diagram 1 shows a saw. The length of the toothed edge is the distance AB.

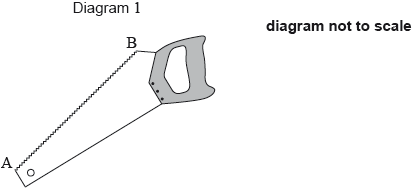
N17/5/MATME/SP2/ENG/TZ0/10.d_01

The toothed edge of the saw can be modelled using the graph of $f$ and the line $L$ . Diagram 2 represents this model.

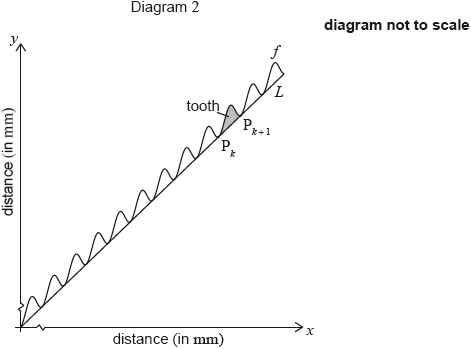
N17/5/MATME/SP2/ENG/TZ0/10.d_02

The shaded part on the graph is called a tooth. A tooth is represented by the region enclosed by the graph of $f$ and the line $L$ , between ${{\text{P}}_k}$ and ${{\text{P}}_{k + 1}}$ .

Show that $f(2\pi ) = 2\pi$ .

[3]

Find the coordinates of ${{\text{P}}_0}$ and of ${{\text{P}}_1}$ .

[3]

b.i.

Find the equation of $L$ .

[3]

b.ii.

Show that the distance between the $x$ -coordinates of ${{\text{P}}_k}$ and ${{\text{P}}_{k + 1}}$ is $2\pi$ .

[2]

A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.

[6]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

substituting $x = 2\pi$ M1

eg $\,\,\,\,\,$ $2\pi + a\sin \left( {2\pi - \frac{\pi }{2}} \right) + a$

$2\pi + a\sin \left( {\frac{{3\pi }}{2}} \right) + a$ (A1)

$2\pi - a + a$ A1

$f(2\pi ) = 2\pi$ AG N0

[3 marks]

substituting the value of $k$ (M1)

${{\text{P}}_0}(0,{\text{ }}0),{\text{ }}{{\text{P}}_1}(2\pi ,{\text{ }}2\pi )$ A1A1 N3

[3 marks]

b.i.

attempt to find the gradient (M1)

eg $\,\,\,\,\,$ $\frac{{2\pi - 0}}{{2\pi - 0}},{\text{ }}m = 1$

correct working (A1)

eg $\,\,\,\,\,$ $\frac{{y - 2\pi }}{{x - 2\pi }} = 1,{\text{ }}b = 0,{\text{ }}y - 0 = 1(x - 0)$

y = x A1 N3

[3 marks]

b.ii.

subtracting $x$ -coordinates of ${{\text{P}}_{k + 1}}$ and ${{\text{P}}_k}$ (in any order) (M1)

eg $\,\,\,\,\,$ $2(k + 1)\pi - 2k\pi ,{\text{ }}2k\pi - 2k\pi - 2\pi$

correct working (must be in correct order) A1

eg $\,\,\,\,\,$ $2k\pi + 2\pi - 2k\pi ,{\text{ }}\left| {2k\pi - 2(k + 1)\pi } \right|$

distance is $2\pi$ AG N0

[2 marks]

METHOD 1

recognizing the toothed-edge as the hypotenuse (M1)

eg $\,\,\,\,\,$ ${300^2} = {x^2} + {y^2}$ , sketch

correct working (using their equation of $L$ (A1)

eg $\,\,\,\,\,$ ${300^2} = {x^2} + {x^2}$

$x = \frac{{300}}{{\sqrt 2 }}$ (exact), 212.132 (A1)

dividing their value of $x$ by $2\pi {\text{ }}\left( {{\text{do not accept }}\frac{{300}}{{2\pi }}} \right)$ (M1)

eg $\,\,\,\,\,$ $\frac{{212.132}}{{2\pi }}$

33.7618 (A1)

33 (teeth) A1 N2

METHOD 2

vertical distance of a tooth is $2\pi$ (may be seen anywhere) (A1)

attempt to find the hypotenuse for one tooth (M1)

eg $\,\,\,\,\,$ ${x^2} = {(2\pi )^2} + {(2\pi )^2}$

$x = \sqrt {8{\pi ^2}}$ (exact), 8.88576 (A1)

dividing 300 by their value of $x$ (M1)

33.7618 (A1)

33 (teeth) A1 N2

[6 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

The Voronoi diagram below shows four supermarkets represented by points with coordinates $A (0, 0)$ , $B (6, 0)$ , $C (0, 6)$ and $D (2, 2)$ . The vertices $X$ , $Y$ , $Z$ are also shown. All distances are measured in kilometres.

The equation of $(XY)$ is $y = 2 - x$ and the equation of $(YZ)$ is $y = 0.5 x + 3.5$ .

The coordinates of $Y$ are $(- 1, 3)$ and the coordinates of $Z$ are $(7, 7)$ .

A town planner believes that the larger the area of the Voronoi cell $XYZ$ , the more people will shop at supermarket $D$ .

Find the midpoint of $[BD]$ .

[2]

Find the equation of $(XZ)$ .

[4]

Find the coordinates of $X$ .

[3]

Determine the exact length of $[YZ]$ .

[2]

Given that the exact length of $[XY]$ is $\sqrt{32}$ , find the size of $XŶZ$ in degrees.

[4]

Hence find the area of triangle $XYZ$ .

[2]

State one criticism of this interpretation.

[1]

Markscheme

$(\frac{2 + 6}{2}, \frac{2 + 0}{2})$ (M1)

$(4, 1)$ A1

Note: Award A0 if parentheses are omitted in the final answer.

[2 marks]

attempt to substitute values into gradient formula (M1)

$(\frac{0 - 2}{6 - 2} =) - \frac{1}{2}$ (A1)

therefore the gradient of perpendicular bisector is $2$ (M1)

so $y - 1 = 2 (x - 4) (y = 2 x - 7)$ A1

[4 marks]

identifying the correct equations to use: (M1)

$y = 2 - x$ and $y = 2 x - 7$

evidence of solving their correct equations or of finding intersection point graphically (M1)

$(3, - 1)$ A1

Note: Accept an answer expressed as “ $x = 3, y = - 1$ ”.

[3 marks]

attempt to use distance formula (M1)

$YZ = \sqrt{{(7 - (- 1))}^{2} + {(7 - 3)}^{2}}$

$= \sqrt{80} (4 \sqrt{5})$ A1

[2 marks]

METHOD 1 (cosine rule)

length of $XZ$ is $\sqrt{80} (4 \sqrt{5}, 8.94427 \dots)$ (A1)

Note: Accept $8.94$ and $8.9$ .

attempt to substitute into cosine rule (M1)

$\cos XŶZ = \frac{80 + 32 - 80}{2 \times \sqrt{80} \sqrt{32}} (= 0.316227 \dots)$ (A1)

Note: Award A1 for correct substitution of $XZ$ , $YZ$ , $\sqrt{32}$ values in the cos rule. Exact values do not need to be used in the substitution.

$(XŶZ =) 71.6 ° (71.5650 \dots °)$ A1

Note: Last A1 mark may be lost if prematurely rounded values of $XZ$ , $YZ$ and/or $XY$ are used.

METHOD 2 (splitting isosceles triangle in half)

length of $XZ$ is $\sqrt{80} (4 \sqrt{5}, 8.94427 \dots)$ (A1)

Note: Accept $8.94$ and $8.9$ .

required angle is $\cos^{- 1} (\frac{\sqrt{32}}{2 \sqrt{80}})$ (M1)(A1)

Note: Award A1 for correct substitution of $XZ$ (or $YZ$ ), $\frac{\sqrt{32}}{2}$ values in the cos rule. Exact values do not need to be used in the substitution.

$(XŶZ =) 71.6 ° (71.5650 \dots °)$ A1

Note: Last A1 mark may be lost if prematurely rounded values of $XZ$ , $YZ$ and/or $XY$ are used.

[4 marks]

(area =) $\frac{1}{2} \sqrt{80} \sqrt{32} \sin 71.5650 \dots$ OR (area =) $\frac{1}{2} \sqrt{32} \sqrt{72}$ (M1)

$= 24 {km}^{2}$ A1

[2 marks]

Any sensible answer such as:

There might be factors other than proximity which influence shopping choices.

A larger area does not necessarily result in an increase in population.

The supermarkets might be specialized / have a particular clientele who visit even if other shops are closer.

Transport links might not be represented by Euclidean distances.

etc. R1

[1 mark]

Examiners report

Part (a) was answered very well and demonstrated that the candidates had good knowledge of the midpoint formula. Some candidates did not write the midpoint they found as a coordinate pair and lost a mark there. Part (b) was answered well. Most candidates were able to find the gradient of [BD] and then the gradient of the perpendicular [XZ] and its equation. Candidates who lost marks in (b) were able to collect follow through marks in parts (c), (d), and (e). In part (c), not all candidates were able to identify the correct equations that they needed to find the coordinates of point X. In part (d), many candidates overlooked the fact that the question called for the exact length of [YZ] – the majority of candidates gave the answer correct to three significant figures and hence lost a mark. In part (d) most candidates were able to correctly use the cosine rule. Marks were lost here if the candidates calculated the length of [XZ] incorrectly, or substituted the [XZ], [YZ] or [XY] values incorrectly. Often candidates used rounded [XZ], [YZ] or [XY] values prematurely, for which they lost the last mark. Part (f) was mostly well answered. If candidates found an angle in part (e), they were usually able to find the area in (f) correctly. Again, the contextual question in part (g) was challenging to many candidates. Some answers showed misconceptions about Voronoi diagrams, for example some candidates stated that “if the cell were larger, then some people living there will be much closer to supermarkets A, B, C than to supermarket D.” Many candidates offered explanations, which were long and unclear, which often did not address the issue they were asked to comment on, nor displayed a sound understanding of the topic.

[N/A]

All lengths in this question are in metres.

Let $f(x) = - 0.8{x^2} + 0.5$ , for $- 0.5 \leqslant x \leqslant 0.5$ . Mark uses $f(x)$ as a model to create a barrel. The region enclosed by the graph of $f$ , the $x$ -axis, the line $x = - 0.5$ and the line $x = 0.5$ is rotated 360° about the $x$ -axis. This is shown in the following diagram.

N16/5/MATME/SP2/ENG/TZ0/06

Use the model to find the volume of the barrel.

[3]

The empty barrel is being filled with water. The volume $V{\text{ }}{{\text{m}}^3}$ of water in the barrel after $t$ minutes is given by $V = 0.8(1 - {{\text{e}}^{ - 0.1t}})$ . How long will it take for the barrel to be half-full?

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to substitute correct limits or the function into the formula involving

${y^2}$

eg $\,\,\,\,\,$ $\pi \int_{ - 0.5}^{0.5} {{y^2}{\text{d}}x,{\text{ }}\pi \int {{{( - 0.8{x^2} + 0.5)}^2}{\text{d}}x} }$

0.601091

volume $= 0.601{\text{ }}({{\text{m}}^3})$ A2 N3

[3 marks]

attempt to equate half their volume to $V$ (M1)

eg $\,\,\,\,\,$ $0.30055 = 0.8(1 - {{\text{e}}^{ - 0.1t}})$ , graph

4.71104

4.71 (minutes) A2 N3

[3 marks]

Examiners report

[N/A]

Let $f\left( x \right) = 12\,\,{\text{cos}}\,x - 5\,\,{\text{sin}}\,x,\,\, - \pi \leqslant x \leqslant 2\pi$ , be a periodic function with $f\left( x \right) = f\left( {x + 2\pi } \right)$

The following diagram shows the graph of $f$ .

There is a maximum point at A. The minimum value of $f$ is −13 .

A ball on a spring is attached to a fixed point O. The ball is then pulled down and released, so that it moves back and forth vertically.

The distance, d centimetres, of the centre of the ball from O at time t seconds, is given by

$d\left( t \right) = f\left( t \right) + 17,\,\,0 \leqslant t \leqslant 5.$

Find the coordinates of A.

[2]

For the graph of $f$ , write down the amplitude.

[1]

b.i.

For the graph of $f$ , write down the period.

[1]

b.ii.

Hence, write $f\left( x \right)$ in the form $p\,\,{\text{cos}}\,\left( {x + r} \right)$ .

[3]

Find the maximum speed of the ball.

[3]

Find the first time when the ball’s speed is changing at a rate of 2 cm s⁻².

[5]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

−0.394791,13

A(−0.395, 13) A1A1 N2

[2 marks]

13 A1 N1

[1 mark]

b.i.

${2\pi }$ , 6.28 A1 N1

[1 mark]

b.ii.

valid approach (M1)

eg recognizing that amplitude is p or shift is r

$f\left( x \right) = 13\,\,{\text{cos}}\,\left( {x + 0.395} \right)$ (accept p = 13, r = 0.395) A1A1 N3

Note: Accept any value of r of the form $0.395 + 2\pi k,\,\,k \in \mathbb{Z}$

[3 marks]

recognizing need for d ′(t) (M1)

eg −12 sin(t) − 5 cos(t)

correct approach (accept any variable for t) (A1)

eg −13 sin(t + 0.395), sketch of d′, (1.18, −13), t = 4.32

maximum speed = 13 (cms⁻¹) A1 N2

[3 marks]

recognizing that acceleration is needed (M1)

eg a(t), d "(t)

correct equation (accept any variable for t) (A1)

eg $a\left( t \right) = - 2,\,\,\left| {\frac{{\text{d}}}{{{\text{d}}t}}\left( {d'\left( t \right)} \right)} \right| = 2,\,\, - 12\,\,{\text{cos}}\,\left( t \right) + 5\,\,{\text{sin}}\,\left( t \right) = - 2$

valid attempt to solve their equation (M1)

eg sketch, 1.33

1.02154

1.02 A2 N3

[5 marks]

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

Consider the function $f\left( x \right) = \frac{1}{3}{x^3} + \frac{3}{4}{x^2} - x - 1$ .

Find $f'\left( x \right)$ .

[3]

Find the gradient of the graph of $y = f\left( x \right)$ at $x = 2$ .

[2]

Find the equation of the tangent line to the graph of $y = f\left( x \right)$ at $x = 2$ . Give the equation in the form $ax + by + d = 0$ where, $a$ , $b$ , and $d \in \mathbb{Z}$ .

[2]

Markscheme

${x^2} + \frac{3}{2}x - 1$ (A1)(A1)(A1)

Note: Award (A1) for each correct term. Award at most (A1)(A1)(A0) if there are extra terms.

[3 marks]

${2^2} + \frac{3}{2} \times 2 - 1$ (M1)

Note: Award (M1) for correct substitution of 2 in their derivative of the function.

6 (A1)(ft)(G2)

Note: Follow through from part (d).

[2 marks]

$\frac{8}{3} = 6\left( 2 \right) + c$ (M1)

Note: Award (M1) for 2, their part (a) and their part (e) substituted into equation of a straight line.

$c = - \frac{{28}}{3}$

$\left( {y - \frac{8}{3}} \right) = 6\left( {x - 2} \right)$ (M1)

Note: Award (M1) for 2, their part (a) and their part (e) substituted into equation of a straight line.

$y = 6x - \frac{{28}}{3}\,\,\left( {y = 6x - 9.33333 \ldots } \right)$ (M1)

Note: Award (M1) for their answer to (e) and intercept $- \frac{{28}}{3}$ substituted in the gradient-intercept line equation.

$- 18x + 3y + 28 = 0$ (accept integer multiples) (A1)(ft)(G2)

Note: Follow through from parts (a) and (e).

[2 marks]

Examiners report

[N/A]

The following diagram shows the graph of $f(x) = a\sin bx + c$ , for $0 \leqslant x \leqslant 12$ .

N16/5/MATME/SP2/ENG/TZ0/10

The graph of $f$ has a minimum point at $(3,{\text{ }}5)$ and a maximum point at $(9,{\text{ }}17)$ .

The graph of $g$ is obtained from the graph of $f$ by a translation of $\left( {\begin{array}{*{20}{c}} k \\ 0 \end{array}} \right)$ . The maximum point on the graph of $g$ has coordinates $(11.5,{\text{ }}17)$ .

The graph of $g$ changes from concave-up to concave-down when $x = w$ .

(i) Find the value of $c$ .

(ii) Show that $b = \frac{\pi }{6}$ .

(iii) Find the value of $a$ .

[6]

(i) Write down the value of $k$ .

(ii) Find $g(x)$ .

[3]

(i) Find $w$ .

(ii) Hence or otherwise, find the maximum positive rate of change of $g$ .

[6]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(i) valid approach (M1)

eg $\,\,\,\,\,$ $\frac{{5 + 17}}{2}$

$c = 11$ A1 N2

(ii) valid approach (M1)

eg $\,\,\,\,\,$ period is 12, per $= \frac{{2\pi }}{b},{\text{ }}9 - 3$

$b = \frac{{2\pi }}{{12}}$ A1

$b = \frac{\pi }{6}$ AG N0

(iii) METHOD 1

valid approach (M1)

eg $\,\,\,\,\,$ $5 = a\sin \left( {\frac{\pi }{6} \times 3} \right) + 11$ , substitution of points

$a = - 6$ A1 N2

METHOD 2

valid approach (M1)

eg $\,\,\,\,\,$ $\frac{{17 - 5}}{2}$ , amplitude is 6

$a = - 6$ A1 N2

[6 marks]

(i) $k = 2.5$ A1 N1

(ii) $g(x) = - 6\sin \left( {\frac{\pi }{6}(x - 2.5)} \right) + 11$ A2 N2

[3 marks]

(i) METHOD 1 Using $g$

recognizing that a point of inflexion is required M1

eg $\,\,\,\,\,$ sketch, recognizing change in concavity

evidence of valid approach (M1)

eg $\,\,\,\,\,$ $g''(x) = 0$ , sketch, coordinates of max/min on ${g'}$

$w = 8.5$ (exact) A1 N2

METHOD 2 Using $f$

recognizing that a point of inflexion is required M1

eg $\,\,\,\,\,$ sketch, recognizing change in concavity

evidence of valid approach involving translation (M1)

eg $\,\,\,\,\,$ $x = w - k$ , sketch, $6 + 2.5$

$w = 8.5$ (exact) A1 N2

(ii) valid approach involving the derivative of $g$ or $f$ (seen anywhere) (M1)

eg $\,\,\,\,\,$ $g'(w),{\text{ }} - \pi \cos \left( {\frac{\pi }{6}x} \right)$ , max on derivative, sketch of derivative

attempt to find max value on derivative M1

eg $\,\,\,\,\,$ $- \pi \cos \left( {\frac{\pi }{6}(8.5 - 2.5)} \right),{\text{ }}f'(6)$ , dot on max of sketch

3.14159

max rate of change $= \pi$ (exact), 3.14 A1 N2

[6 marks]

Examiners report

[N/A]

A theatre set designer is designing a piece of flat scenery in the shape of a hill. The scenery is formed by a curve between two vertical edges of unequal height. One edge is $2$ metres high and the other is $1$ metre high. The width of the scenery is $6$ metres.

A coordinate system is formed with the origin at the foot of the $2$ metres high edge. In this coordinate system the highest point of the cross‐section is at $(2, 3.5)$ .

A set designer wishes to work out an approximate value for the area of the scenery $(A m^{2})$ .

In order to obtain a more accurate measure for the area the designer decides to model the curved edge with the polynomial $h (x) = a x^{3} + b x^{2} + c x + d a, b, c, d \in ℝ$ where $h$ metres is the height of the curved edge a horizontal distance $x m$ from the origin.

Explain why $A < 21$ .

[1]

By dividing the area between the curve and the $x$ ‐axis into two trapezoids of unequal width show that $A > 14.5$ , justifying the direction of the inequality.

[4]

Write down the value of $d$ .

[1]

Use differentiation to show that $12 a + 4 b + c = 0$ .

[2]

Determine two other linear equations in $a$ , $b$ and $c$ .

[3]

Hence find an expression for $h (x)$ .

[3]

Use the expression found in (f) to calculate a value for $A$ .

[2]

Markscheme

The area $A$ is less than the rectangle containing the cross-section which is equal to $6 \times 3.5 = 21$ R1

Note: $6 \times 3.5 = 21$ is not sufficient for R1.

[1 mark]

$\frac{1}{2} \times 2 \times (2 + 3.5) + \frac{1}{2} \times 4 \times (3.5 + 1)$ (M1)(A1)

$= 14.5$ A1

This is an underestimate as the trapezoids are enclosed by (are under) the curve. R1

Note: This can be shown in a diagram.

[4 marks]

$h (0) = 2 \Rightarrow d = 2$ A1

[1 mark]

$h' (x) = 3 a x^{2} + 2 b x + c$ A1

$h' (2) = 0$ M1

hence $12 a + 4 b + c = 0$ AG

[2 marks]

Substitute the points $(2, 3.5)$ and $(6, 1)$ (M1)

$8 a + 4 b + 2 c + 2 = 3.5 (8 a + 4 b + 2 c = 1.5)$

and

$216 a + 36 b + 6 c + 2 = 1 (216 a + 36 b + 6 c = - 1)$ A1A1

[3 marks]

Solve on a GDC (M1)

$h (x) = 0.0365 x^{3} - 0.521 x^{2} + 1.65 x + 2$ A2

$(h (x) = 0.0364583 \dots x^{3} - 0.520833 \dots x^{2} + 1.64583 \dots x + 2)$

[3 marks]

$\int_{0}^{6} 0.0364583 \dots x^{3} - 0.520833 \dots x^{2} + 1.64583 \dots x + 2 d x$

$= 15.9 (15.9374 \dots) (m^{2})$ (M1)A1

Note: Accept $16.0 (16.014)$ from the three significant figure answer to part (g).

[2 marks]

Examiners report

[N/A]

At an amusement park, a Ferris wheel with diameter 111 metres rotates at a constant speed. The bottom of the wheel is k metres above the ground. A seat starts at the bottom of the wheel.

The wheel completes one revolution in 16 minutes.

After t minutes, the height of the seat above ground is given by $h\left( t \right) = 61.5 + a\,{\text{cos}}\left( {\frac{\pi }{8}t} \right)$ , for 0 ≤ t ≤ 32.

Find when the seat is 30 m above the ground for the third time.

Markscheme

valid approach (M1)
eg sketch of h and $y = 30,\,\,h = 30,\,\,61.5 - 55.5\,{\text{cos}}\left( {\frac{\pi }{8}t} \right) = 30,\,\,t = 2.46307,\,\,t = 13.5369$

18.4630

t = 18.5 (minutes) A1 N3

[3 marks]

Examiners report

[N/A]

A new concert hall was built with $14$ seats in the first row. Each subsequent row of the hall has two more seats than the previous row. The hall has a total of $20$ rows.

Find:

The concert hall opened in $2019$ . The average number of visitors per concert during that year was $584$ . In $2020$ , the average number of visitors per concert increased by $1.2 %$ .

The concert organizers use this data to model future numbers of visitors. It is assumed that the average number of visitors per concert will continue to increase each year by $1.2 %$ .

the number of seats in the last row.

[3]

a.i.

the total number of seats in the concert hall.

[2]

a.ii.

Find the average number of visitors per concert in $2020$ .

[2]

Determine the first year in which this model predicts the average number of visitors per concert will exceed the total seating capacity of the concert hall.

[5]

It is assumed that the concert hall will host $50$ concerts each year.

Use the average number of visitors per concert per year to predict the total number of people expected to attend the concert hall from when it opens until the end of $2025$ .

[4]

Markscheme

recognition of arithmetic sequence with common difference $2$ (M1)

use of arithmetic sequence formula (M1)

$14 + 2 (20 - 1)$

$52$ A1

[3 marks]

a.i.

use of arithmetic series formula (M1)

$\frac{14 + 52}{2} \times 20$

$660$ A1

[2 marks]

a.ii.

$584 + (584 \times 0.012)$ OR $584 \times {(1.012)}^{1}$ (M1)

$591 (591.008)$ A1

Note: Award M0A0 if incorrect $r$ used in part (b), and FT with their $r$ in parts (c) and (d).

[2 marks]

recognition of geometric sequence (M1)

equating their $n$ th geometric sequence term to their $660$ (M1)

Note: Accept inequality.

METHOD 1

EITHER

$600 = 584 \times {(1.012)}^{x - 1}$ A1

$(x - 1 =) 10.3 (10.2559 \dots)$

$x = 11.3 (11.2559 \dots)$ A1

$2030$ A1

$600 = 584 \times {(1.012)}^{x}$ A1

$x = 10.3 (10.2559 \dots)$ A1

$2030$ A1

METHOD 2

11^th term $658 (657.987 \dots)$ (M1)A1

12^th term $666 (666.883 \dots)$ (M1)A1

$2030$ A1

Note: The last mark can be awarded if both their 11^th and 12^th correct terms are seen.

[5 marks]

$7$ seen (A1)

EITHER

$584 (\frac{1 . 012^{7} - 1}{1.012 - 1})$ (M1)

multiplying their sum by $50$ (M1)

sum of the number of visitors for their $r$ and their seven years (M1)

multiplying their sum by $50$ (M1)

$29 200 (\frac{1 . 012^{7} - 1}{1.012 - 1})$ (M1)(M1)

THEN

$212000 (211907.3 \dots)$ A1

Note: Follow though from their $r$ from part (b).

[4 marks]

Examiners report

[N/A]

a.i.

[N/A]

a.ii.

[N/A]

The following diagram shows the graph of a function $y = f(x)$ , for $- 6 \leqslant x \leqslant - 2$ .

The points $( - 6,{\text{ }}6)$ and $( - 2,{\text{ }}6)$ lie on the graph of $f$ . There is a minimum point at $( - 4,{\text{ }}0)$ .

Write down the range of $f$ .

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

correct interval A2 N2

eg $\,\,\,\,\,$ $0 \leqslant y \leqslant 6,{\text{ }}[0,{\text{ }}6]$ , from 0 to 6

[2 marks]

Examiners report

[N/A]

A hollow chocolate box is manufactured in the form of a right prism with a regular hexagonal base. The height of the prism is $h cm$ , and the top and base of the prism have sides of length $x cm$ .

Given that $\sin 60 ° = \frac{\sqrt{3}}{2}$ , show that the area of the base of the box is equal to $\frac{3 \sqrt{3} x^{2}}{2}$ .

[2]

Given that the total external surface area of the box is $1200 {cm}^{2}$ , show that the volume of the box may be expressed as $V = 300 \sqrt{3} x - \frac{9}{4} x^{3}$ .

[5]

Sketch the graph of $V = 300 \sqrt{3} x - \frac{9}{4} x^{3}$ , for $0 \leq x \leq 16$ .

[2]

Find an expression for $\frac{d V}{d x}$ .

[2]

Find the value of $x$ which maximizes the volume of the box.

[2]

Hence, or otherwise, find the maximum possible volume of the box.

[2]

The box will contain spherical chocolates. The production manager assumes that they can calculate the exact number of chocolates in each box by dividing the volume of the box by the volume of a single chocolate and then rounding down to the nearest integer.

Explain why the production manager is incorrect.

[1]

Markscheme

evidence of splitting diagram into equilateral triangles M1

area $= 6 (\frac{1}{2} x^{2} \sin 60 °)$ A1

$= \frac{3 \sqrt{3} x^{2}}{2}$ AG

Note: The AG line must be seen for the final A1 to be awarded.

[2 marks]

total surface area of prism $1200 = 2 (3 x^{2} \frac{\sqrt{3}}{2}) + 6 x h$ M1A1

Note: Award M1 for expressing total surface areas as a sum of areas of rectangles and hexagons, and A1 for a correctly substituted formula, equated to $1200$ .

$h = \frac{400 - \sqrt{3} x^{2}}{2 x}$ A1

volume of prism $= \frac{3 \sqrt{3}}{2} x^{2} \times h$ (M1)

$= \frac{3 \sqrt{3}}{2} x^{2} (\frac{400 - \sqrt{3} x^{2}}{2 x})$ A1

$= 300 \sqrt{3} x - \frac{9}{4} x^{3}$ AG

Note: The AG line must be seen for the final A1 to be awarded.

[5 marks]

A1A1

Note: Award A1 for correct shape, A1 for roots in correct place with some indication of scale (indicated by a labelled point).

[2 marks]

$\frac{d V}{d x} = 300 \sqrt{3} - \frac{27}{4} x^{2}$ A1A1

Note: Award A1 for a correct term.

[2 marks]

from the graph of $V$ or $\frac{d V}{d x}$ OR solving $\frac{d V}{d x} = 0$ (M1)

$x = 8.88 (8.877382 \dots)$ A1

[2 marks]

from the graph of $V$ OR substituting their value for $x$ into $V$ (M1)

$V_{max} = 3040 {cm}^{3} (3039.34 \dots)$ A1

[2 marks]

EITHER
wasted space / spheres do not pack densely (tesselate) A1

OR
the model uses exterior values / assumes infinite thinness of materials and hence the modelled volume is not the true volume A1

[1 mark]

Examiners report

[N/A]