An ice-skater is skating such that her position vector when viewed from above at time $t$ seconds can be modelled by

$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}a {\text{e}}^{bt}\cos t\\ a {\text{e}}^{bt}\text{\hspace{0.05em}sin} t\end{array}\right)$

with respect to a rectangular coordinate system from a point $\text{O}$, where the non-zero constants $a$ and $b$ can be determined. All distances are in metres.

At time $t=0$, the displacement of the ice-skater is given by $\left(\begin{array}{c}5\\ 0\end{array}\right)$ and the velocity of the ice‑skater is given by $\left(\begin{array}{c}-3.5\\ 5\end{array}\right)$.

A flying drone is programmed to complete a series of movements in a horizontal plane relative to an origin $\text{O}$ and a set of $x$-$y$-axes.

In each case, the drone moves to a new position represented by the following transformations:

• a rotation anticlockwise of $\frac{\mathrm{\pi }}{6}$ radians about $\text{O}$
• a reflection in the line $y=\frac{x}{\sqrt{3}}$
• a rotation clockwise of $\frac{\mathrm{\pi }}{3}$ radians about $\text{O}$.

All the movements are performed in the listed order.

A ball is attached to the end of a string and spun horizontally. Its position relative to a given point, $\text{O}$, at time $t$ seconds, $t\ge 0$, is given by the equation

$\mathit{r}=\left(\begin{array}{c}1.5 \cos (0.1t^2)\\ 1.5 \sin (0.1t^2)\end{array}\right)$ where all displacements are in metres.

The string breaks when the magnitude of the ball’s acceleration exceeds $20 {\text{ms}}^{-2}$.

A transformation, $T$, of a plane is represented by $\mathit{r}\prime =\mathit{P}\mathit{r}+\mathit{q}$, where $\mathit{P}$ is a $2 \times 2$ matrix, $\mathit{q}$ is a $2 \times 1$ vector, $\mathit{r}$ is the position vector of a point in the plane and $\mathit{r}\prime$ the position vector of its image under $T$.

The triangle $\text{OAB}$ has coordinates $(0, 0)$, $(0, 1)$ and $(1, 0)$. Under T, these points are transformed to $(0, 1)$, $\left(\frac{1}{4}, 1+\frac{\sqrt{3}}{4}\right)$ and $\left(\frac{\sqrt{3}}{4}, \frac{3}{4}\right)$ respectively.

$\mathit{P}$ can be written as $\mathit{P}=\mathit{R}\mathit{S}$, where $\mathit{S}$ and $\mathit{R}$ are matrices.

$\mathit{S}$ represents an enlargement with scale factor $0.5$, centre $(0, 0)$.

$\mathit{R}$ represents a rotation about $(0, 0)$.

The transformation $T$ can also be described by an enlargement scale factor $\frac{1}{2}$, centre $(a, b)$, followed by a rotation about the same centre $(a, b)$.

A sector of a circle, centre $\text{O}$ and radius $4.5 \text{m}$, is shown in the following diagram.

A square field with side $8 \text{m}$ has a goat tied to a post in the centre by a rope such that the goat can reach all parts of the field up to $4.5 \text{m}$ from the post.

^{[Source: mynamepong, n.d. Goat [image online] Available at: https://thenounproject.com/term/goat/1761571/
This file is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)
https://creativecommons.org/licenses/by-sa/3.0/deed.en [Accessed 22 April 2010] Source adapted.]}

Let $V$ be the volume of grass eaten by the goat, in cubic metres, and $t$ be the length of time, in hours, that the goat has been in the field.

The goat eats grass at the rate of $\frac{dV}{dt}=0.3 t{\text{e}}^{-t}$.

Consider the curve $y=\sqrt{x}$.

The shape of a piece of metal can be modelled by the region bounded by the functions $f$, $g$, the $x$-axis and the line segment $\text{[AB]}$, as shown in the following diagram. The units on the $x$ and $y$ axes are measured in metres.

The piecewise function $f$ is defined by

$f\left(x\right)=\{\begin{array}{cc}\sqrt{x} & 0\le x\le 0.16\\ 1.25x+0.2 & 0.16<x\le 0.5\end{array}$

The graph of $g$ is obtained from the graph of $f$ by:

• a stretch scale factor of $\frac{1}{2}$ in the $x$ direction,
• followed by a stretch scale factor $\frac{1}{2}$ in the $y$ direction,
• followed by a translation of $0.2$ units to the right.

Point $\text{A}$ lies on the graph of $f$ and has coordinates $(0.5, 0.825)$. Point $\text{B}$ is the image of $\text{A}$ under the given transformations and has coordinates $(p, q)$.

The piecewise function $g$ is given by

$g\left(x\right)=\{\begin{array}{cc}h\left(x\right) & 0.2\le x\le a\\ 1.25x+b & a<x\le p\end{array}$

The area enclosed by $y=g\left(x\right)$, the $x$-axis and the line $x=p$ is $0.0627292 {\text{m}}^2$ correct to six significant figures.

The cost adjacency matrix for the complete graph K₆ is given below.

It represents the distances in kilometres along dusty tracks connecting villages on an island. Find the minimum spanning tree for this graph; in all 3 cases state the order in which the edges are added.

It is desired to tarmac some of these tracks so that it is possible to walk from any village to any other village walking entirely on tarmac.

At an archery tournament, a particular competition sees a ball launched into the air while an archer attempts to hit it with an arrow.

The path of the ball is modelled by the equation

$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}5\\ 0\end{array}\right)+t\left(\begin{array}{c}{u}_x\\ u_y-5t\end{array}\right)$

where $x$ is the horizontal displacement from the archer and $y$ is the vertical displacement from the ground, both measured in metres, and $t$ is the time, in seconds, since the ball was launched.

• $u_x$ is the horizontal component of the initial velocity
• $u_y$ is the vertical component of the initial velocity.

In this question both the ball and the arrow are modelled as single points. The ball is launched with an initial velocity such that $u_x=8$ and $u_y=10$.

An archer releases an arrow from the point $(0, 2)$. The arrow is modelled as travelling in a straight line, in the same plane as the ball, with speed $60 {\text{m\hspace{0.05em}s}}^{-1}$ and an angle of elevation of $10°$.

The matrices A and B are defined by  and .

Triangle X is mapped onto triangle Y by the transformation represented by AB. The coordinates of triangle Y are (0, 0), (−30, −20) and (−16, 32).

Let G be the graph below.

The matrix A is defined by .

Pentagon, P, which has an area of 7 cm², is transformed by A.

The matrix B is defined by .

B represents the combined effect of the transformation represented by a matrix X, followed by the transformation represented by A.

In triangle $\text{PQR, PR}=12\text{ cm, QR}=p\text{ cm, PQ}=r\text{ cm}$ and $\mathrm{Q}\stackrel{^<!--\; ^\; -->}{\mathrm{P}}\mathrm{R}={30}^{\circ <!--\; \circ \; -->}$.

Consider the possible triangles with $\text{QR}=8\text{ cm}$.

Consider the case where $p$, the length of QR is not fixed at 8 cm.

A water trough which is 10 metres long has a uniform cross-section in the shape of a semicircle with radius 0.5 metres. It is partly filled with water as shown in the following diagram of the cross-section. The centre of the circle is O and the angle KOL is $\mathrm{\theta <!--\; \theta \; -->}$ radians.

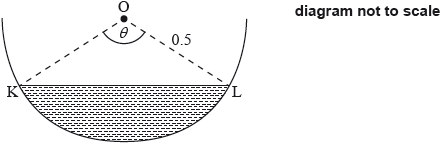
The volume of water is increasing at a constant rate of $0.0008{\text{m}}^3{\text{s}}^{-<!--\; -\; -->1}$.

An aircraft’s position is given by the coordinates ($x$, $y$, $z$), where $x$ and $y$ are the aircraft’s displacement east and north of an airport, and $z$ is the height of the aircraft above the ground. All displacements are given in kilometres.

The velocity of the aircraft is given as $\left(\begin{array}{c}-<!--\; -\; -->150\\ -<!--\; -\; -->50\\ -<!--\; -\; -->20\end{array}\right)\text{km}{\text{h}}^{-<!--\; -\; -->1}$.

At 13:00 it is detected at a position 30 km east and 10 km north of the airport, and at a height of 5 km. Let $t$ be the length of time in hours from 13:00.

If the aircraft continued to fly with the velocity given

When the aircraft is 4 km above the ground it continues to fly on the same bearing but adjusts the angle of its descent so that it will land at the point (0, 0, 0).

Two submarines A and B have their routes planned so that their positions at time t hours, 0 ≤ t < 20 , would be defined by the position vectors r_A $=\left(\begin{array}{c}2\\ 4\\ -<!--\; -\; -->1\end{array}\right)+t\left(\begin{array}{c}-<!--\; -\; -->1\\ 1\\ -<!--\; -\; -->0.15\end{array}\right)$ and r_B $=\left(\begin{array}{c}0\\ 3.2\\ -<!--\; -\; -->2\end{array}\right)+t\left(\begin{array}{c}-<!--\; -\; -->0.5\\ 1.2\\ 0.1\end{array}\right)$ relative to a fixed point on the surface of the ocean (all lengths are in kilometres).

To avoid the collision submarine B adjusts its velocity so that its position vector is now given by

r_B $=\left(\begin{array}{c}0\\ 3.2\\ -<!--\; -\; -->2\end{array}\right)+t\left(\begin{array}{c}-<!--\; -\; -->0.45\\ 1.08\\ 0.09\end{array}\right)$.

A canal system divides a city into six land masses connected by fifteen bridges, as shown in the diagram below.

State with reasons whether or not this graph has

The following table shows the costs in US dollars (US$) of direct flights between six cities. Blank cells indicate no direct flights. The rows represent the departure cities. The columns represent the destination cities.

The following table shows the least cost to travel between the cities.

A travelling salesman has to visit each of the cities, starting and finishing at city A.

The adjacency matrix of the graph G, with vertices P, Q, R, S, T is given by:

Consider the following diagram.

The sides of the equilateral triangle ABC have lengths 1 m. The midpoint of [AB] is denoted by P. The circular arc AB has centre, M, the midpoint of [CP].

The diagram shows two circles with centres at the points A and B and radii $2r$ and $r$, respectively. The point B lies on the circle with centre A. The circles intersect at the points C and D.

Let $\mathrm{\alpha <!--\; \alpha \; -->}$ be the measure of the angle CAD and $\mathrm{\theta <!--\; \theta \; -->}$ be the measure of the angle CBD in radians.

In a triangle $\text{ABC, AB}=4\text{ cm, BC}=3\text{ cm}$ and $\mathrm{B}\stackrel{^<!--\; ^\; -->}{\mathrm{A}}\mathrm{C}=\frac{\mathrm{\pi <!--\; \pi \; -->}}{9}$.