IB Questionbank

Updates to Questionbank

User interface language: English | Español

HL Paper 3

$G$ is a simple, connected, planar graph with $9$ vertices and $e$ edges.

The complement of $G$ has $e'$ edges.

Find the maximum possible value of $e$ .

[2]

Find an expression for $e'$ in terms of $e$ .

[2]

Given that the complement of $G$ is also planar and connected, find the possible values of $e$ .

[2]

$H$ is a simple graph with $v$ vertices and $e$ edges.

Given that both $H$ and its complement are planar and connected, find the maximum possible value of $v$ .

[5]

Christine and her friends live in Winnipeg, Canada. The weighted graph shows the location of their houses and the time, in minutes, to travel between each house.

Christine’s house is located at vertex $C$ .

Use Dijkstra’s algorithm to find the shortest time to travel from $C$ to $F$ , clearly showing how the algorithm has been applied.

[6]

a.i.

Hence write down the shortest path from $C$ to $F$ .

[1]

a.ii.

A new road is constructed that allows Christine to travel from $H$ to $A$ in $t$ minutes. If Christine starts from home and uses this new road her minimum travel time to $A$ is reduced, but her minimum travel time to $F$ remains the same.

Find the possible values of $t$ .

[5]

This question explores how graph algorithms can be applied to a graph with an unknown edge weight.

Graph $W$ is shown in the following diagram. The vertices of $W$ represent tourist attractions in a city. The weight of each edge represents the travel time, to the nearest minute, between two attractions. The route between $A$ and $F$ is currently being resurfaced and this has led to a variable travel time. For this reason, $AF$ has an unknown travel time $x$ minutes, where $x \in ℤ^{+}$ .

Daniel plans to visit all the attractions, starting and finishing at $A$ . He wants to minimize his travel time.

To find a lower bound for Daniel’s travel time, vertex $A$ and its adjacent edges are first deleted.

Daniel makes a table to show the minimum travel time between each pair of attractions.

Write down the value of

To find an upper bound for Daniel’s travel time, the nearest neighbour algorithm is used, starting at vertex $A$ .

Consider the case where $x = 3$ .

Consider the case where $x > 3$ .

Write down a Hamiltonian cycle in $W$ .

[1]

Use Prim’s algorithm, starting at vertex $B$ , to find the weight of the minimum spanning tree of the remaining graph. You should indicate clearly the order in which the algorithm selects each edge.

[5]

b.i.

Hence, for the case where $x < 9$ , find a lower bound for Daniel’s travel time, in terms of $x$ .

[2]

b.ii.

$p$ .

[1]

c.i.

$q$ .

[1]

c.ii.

$r$ .

[1]

c.iii.

Use the nearest neighbour algorithm to find two possible cycles.

[3]

d.i.

Find the best upper bound for Daniel’s travel time.

[2]

d.ii.

Find the least value of $x$ for which the edge $AF$ will definitely not be used by Daniel.

[2]

e.i.

Hence state the value of the upper bound for Daniel’s travel time for the value of $x$ found in part (e)(i).

[2]

e.ii.

The tourist office in the city has received complaints about the lack of cleanliness of some routes between the attractions. Corinne, the office manager, decides to inspect all the routes between all the attractions, starting and finishing at $H$ . The sum of the weights of all the edges in graph $W$ is $(92 + x)$ .

Corinne inspects all the routes as quickly as possible and takes $2$ hours.

Find the value of $x$ during Corinne’s inspection.

[5]

A graphic designer, Ben, wants to create an animation in which a sequence of squares is created by a composition of successive enlargements and translations and then rotated about the origin and reduced in size.

Ben outlines his plan with the following storyboards.

The first four frames of the animation are shown below in greater detail.

The sides of each successive square are one half the size of the adjacent larger square. Let the sequence of squares be $U_{0}, U_{1}, U_{2}, \dots$

The first square, $U_{0}$ , has sides of length $4 cm$ .

Ben decides the animation will continue as long as the width of the square is greater than the width of one pixel.

Ben decides to generate the squares using the transformation

$(\begin{matrix} x_{n} \\ y_{n} \end{matrix}) = A_{n} (\begin{matrix} x_{0} \\ y_{0} \end{matrix}) + b_{n}$

where $A_{n}$ is a $2 \times 2$ matrix that represents an enlargement, $b_{n}$ is a $2 \times 1$ column vector that represents a translation, $(x_{0}, y_{0})$ is a point in $U_{0}$ and $(x_{n}, y_{n})$ is its image in $U_{n}$ .

By considering the case where $(x_{0}, y_{0})$ is $(0, 0)$ ,

Once the image of squares has been produced, Ben wants to continue the animation by rotating the image counter clockwise about the origin and having it reduce in size during the rotation.

Let $E_{θ}$ be the enlargement matrix used when the original sequence of squares has been rotated through $θ$ degrees.

Ben decides the enlargement scale factor, $s$ , should be a linear function of the angle, $θ$ , and after a rotation of $360 °$ the sequence of squares should be half of its original length.

Find an expression for the width of $U_{n}$ in centimetres.

[2]

Given the width of a pixel is approximately $0.025 cm$ , find the number of squares in the final image.

[3]

Write down $A_{1}$ .

[1]

c.i.

Write down $A_{n}$ , in terms of $n$ .

[1]

c.ii.

state the coordinates, $(x_{1}, y_{1})$ , of its image in $U_{1}$ .

[1]

d.i.

hence find $b_{1}$ .

[2]

d.ii.

show that $b_{n} = (\begin{matrix} 8 (1 - 2^{- n}) \\ 8 (1 - 2^{- n}) \end{matrix})$ .

[3]

d.iii.

Hence or otherwise, find the coordinates of the top left-hand corner in $U_{7}$ .

[3]

Find, $s$ , in the form $s (θ) = m θ + c$ .

[4]

f.i.

Write down $E_{θ}$ .

[1]

f.ii.

Hence find the image of $(1, 1)$ after it is rotated $135 °$ and enlarged.

[4]

f.iii.

Find the value of $θ$ at which the enlargement scale factor equals zero.

[1]

After the enlargement scale factor equals zero, Ben continues to rotate the image for another two revolutions.

Describe the animation for these two revolutions, stating the final position of the sequence of squares.

[3]

This question is about a metropolitan area council planning a new town and the location of a new toxic waste dump.

A metropolitan area in a country is modelled as a square. The area has four towns, located at the corners of the square. All units are in kilometres with the $x$ -coordinate representing the distance east and the $y$ -coordinate representing the distance north from the origin at $(0, 0)$ .

Edison is modelled as being positioned at $E (0, 40)$ .
Fermitown is modelled as being positioned at $F (40, 40)$ .
Gaussville is modelled as being positioned at $G (40, 0)$ .
Hamilton is modelled as being positioned at $H (0, 0)$ .

The metropolitan area council decides to build a new town called Isaacopolis located at $I (30, 20)$ .

A new Voronoi diagram is to be created to include Isaacopolis. The equation of the perpendicular bisector of $[IE]$ is $y = \frac{3}{2} x + \frac{15}{2}$ .

The metropolitan area is divided into districts based on the Voronoi regions found in part (c).

A toxic waste dump needs to be located within the metropolitan area. The council wants to locate it as far as possible from the nearest town.

The toxic waste dump, $T$ , is connected to the towns via a system of sewers.

The connections are represented in the following matrix, $M$ , where the order of rows and columns is ( $E, F, G, H, I, T$ ).

$M = (\begin{matrix} 1 & 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \end{matrix})$

A leak occurs from the toxic waste dump and travels through the sewers. The pollution takes one day to travel between locations that are directly connected.

The digit $1$ in $M$ represents a direct connection. The values of $1$ in the leading diagonal of $M$ mean that once a location is polluted it will stay polluted.

The model assumes that each town is positioned at a single point. Describe possible circumstances in which this modelling assumption is reasonable.

[1]

Sketch a Voronoi diagram showing the regions within the metropolitan area that are closest to each town.

[1]

Find the equation of the perpendicular bisector of $[IF]$ .

[4]

c.i.

Given that the coordinates of one vertex of the new Voronoi diagram are $(20, 37.5)$ , find the coordinates of the other two vertices within the metropolitan area.

[4]

c.ii.

Sketch this new Voronoi diagram showing the regions within the metropolitan area which are closest to each town.

[2]

c.iii.

A car departs from a point due north of Hamilton. It travels due east at constant speed to a destination point due North of Gaussville. It passes through the Edison, Isaacopolis and Fermitown districts. The car spends $30 %$ of the travel time in the Isaacopolis district.

Find the distance between Gaussville and the car’s destination point.

[4]

Find the location of the toxic waste dump, given that this location is not on the edge of the metropolitan area.

[4]

e.i.

Make one possible criticism of the council’s choice of location.

[1]

e.ii.

Find which town is last to be polluted. Justify your answer.

[3]

f.i.

Write down the number of days it takes for the pollution to reach the last town.

[1]

f.ii.

A sewer inspector needs to plan the shortest possible route through each of the connections between different locations. Determine an appropriate start point and an appropriate end point of the inspection route.

Note that the fact that each location is connected to itself does not correspond to a sewer that needs to be inspected.

[2]

f.iii.

This question compares possible designs for a new computer network between multiple school buildings, and whether they meet specific requirements.

A school’s administration team decides to install new fibre-optic internet cables underground. The school has eight buildings that need to be connected by these cables. A map of the school is shown below, with the internet access point of each building labelled $A–H$ .

Jonas is planning where to install the underground cables. He begins by determining the distances, in metres, between the underground access points in each of the buildings.

He finds $AD = 89.2 m$ , $DF = 104.9 m$ and $A \hat{D} F = 83 °$ .

The cost for installing the cable directly between $A$ and $F$ is $$ 21 310$ .

Jonas estimates that it will cost $$ 110$ per metre to install the cables between all the other buildings.

Jonas creates the following graph, $S$ , using the cost of installing the cables between two buildings as the weight of each edge.

The computer network could be designed such that each building is directly connected to at least one other building and hence all buildings are indirectly connected.

The computer network fails if any part of it becomes unreachable from any other part. To help protect the network from failing, every building could be connected to at least two other buildings. In this way if one connection breaks, the building is still part of the computer network. Jonas can achieve this by finding a Hamiltonian cycle within the graph.

After more research, Jonas decides to install the cables as shown in the diagram below.

Each individual cable is installed such that each end of the cable is connected to a building’s access point. The connection between each end of a cable and an access point has a $1.4 %$ probability of failing after a power surge.

For the network to be successful, each building in the network must be able to communicate with every other building in the network. In other words, there must be a path that connects any two buildings in the network. Jonas would like the network to have less than a $2 %$ probability of failing to operate after a power surge.

Find $AF$ .

[3]

Find the cost per metre of installing this cable.

[2]

State why the cost for installing the cable between $A$ and $F$ would be higher than between the other buildings.

[1]

By using Kruskal’s algorithm, find the minimum spanning tree for $S$ , showing clearly the order in which edges are added.

[3]

d.i.

Hence find the minimum installation cost for the cables that would allow all the buildings to be part of the computer network.

[2]

d.ii.

State why a path that forms a Hamiltonian cycle does not always form an Eulerian circuit.

[1]

Starting at $D$ , use the nearest neighbour algorithm to find the upper bound for the installation cost of a computer network in the form of a Hamiltonian cycle.

Note: Although the graph is not complete, in this instance it is not necessary to form a table of least distances.

[5]

By deleting $D$ , use the deleted vertex algorithm to find the lower bound for the installation cost of the cycle.

[6]

Show that Jonas’s network satisfies the requirement of there being less than a $2 %$ probability of the network failing after a power surge.

[5]

The weights of the edges in the complete graph $G$ are given in the following table.

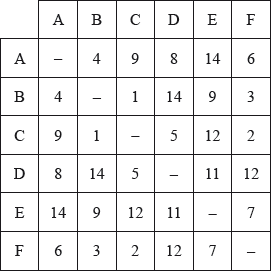
M17/5/MATHL/HP3/ENG/TZ0/DM/02

Starting at A , use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for $G$ .

[5]

By first deleting vertex A , use the deleted vertex algorithm together with Kruskal’s algorithm to find a lower bound for the travelling salesman problem for $G$ .

[7]

Consider the graph G represented in the following diagram.

The graph G is a plan of a holiday resort where each vertex represents a villa and the edges represent the roads between villas. The weights of the edges are the times, in minutes, Mr José, the security guard, takes to walk along each of the roads. Mr José is based at villa A.

State, with a reason, whether or not G has an Eulerian circuit.

[1]

Use Kruskal’s algorithm to find a minimum spanning tree for G, stating its total weight. Indicate clearly the order in which the edges are added.

[4]

Use a suitable algorithm to show that the minimum time in which Mr José can get from A to E is 13 minutes.

[5]

Find the minimum time it takes Mr José to patrol the resort if he has to walk along every road at least once, starting and ending at A. State clearly which roads need to be repeated.

[7]

In the context of graph theory, explain briefly what is meant by a circuit;

[1]

a.i.

In the context of graph theory, explain briefly what is meant by an Eulerian circuit.

[1]

a.ii.

The graph $G$ has six vertices and an Eulerian circuit. Determine whether or not its complement $G^{'}$ can have an Eulerian circuit.

[3]

Find an example of a graph $H$ , with five vertices, such that $H$ and its complement $H^{'}$ both have an Eulerian trail but neither has an Eulerian circuit. Draw $H$ and $H^{'}$ as your solution.

[4]

Consider the following weighted graph G.

State what feature of G ensures that G has an Eulerian trail.

[1]

a.i.

State what feature of G ensures that G does not have an Eulerian circuit.

[1]

a.ii.

Write down an Eulerian trail in G.

[2]

Starting and finishing at B, find a solution to the Chinese postman problem for G.

[3]

c.ii.

Calculate the total weight of the solution.

[1]

c.iii.

Mathilde delivers books to five libraries, A, B, C, D and E. She starts her deliveries at library D and travels to each of the other libraries once, before returning to library D. Mathilde wishes to keep her travelling distance to a minimum.

The weighted graph $H$ , representing the distances, measured in kilometres, between the five libraries, has the following table.

N17/5/MATHL/HP3/ENG/TZ0/DM/01

Draw the weighted graph $H$ .

[2]

Starting at library D use the nearest-neighbour algorithm, to find an upper bound for Mathilde’s minimum travelling distance. Indicate clearly the order in which the edges are selected.

[5]

By first removing library C, use the deleted vertex algorithm, to find a lower bound for Mathilde’s minimum travelling distance.

[4]

The simple, complete graph ${\kappa _n}(n > 2)$ has vertices ${{\text{A}}_1},{\text{ }}{{\text{A}}_2},{\text{ }}{{\text{A}}_3},{\text{ }} \ldots ,{\text{ }}{{\text{A}}_n}$ . The weight of the edge from ${{\text{A}}_i}$ to ${{\text{A}}_j}$ is given by the number $i + j$ .

Consider the general graph ${\kappa _n}$ .

(i) Draw the graph ${\kappa _4}$ including the weights of all the edges.

(ii) Use the nearest-neighbour algorithm, starting at vertex ${{\text{A}}_1}$ , to find a Hamiltonian cycle.

(iii) Hence, find an upper bound to the travelling salesman problem for this weighted graph.

[4]

Consider the graph ${\kappa _5}$ . Use the deleted vertex algorithm, with ${{\text{A}}_5}$ as the deleted vertex, to find a lower bound to the travelling salesman problem for this weighted graph.

[5]

(i) Use the nearest-neighbour algorithm, starting at vertex ${{\text{A}}_1}$ , to find a Hamiltonian cycle.

(ii) Hence find and simplify an expression in $n$ , for an upper bound to the travelling salesman problem for this weighted graph.

[7]

By splitting the weight of the edge ${{\text{A}}_i}{{\text{A}}_j}$ into two parts or otherwise, show that all Hamiltonian cycles of ${\kappa _n}$ have the same total weight, equal to the answer found in (c)(ii).

[3]

$G$ is a simple, connected graph with eight vertices.

$H$ is a connected, planar graph, with $v$ vertices, $e$ edges and $f$ faces. Every face in $H$ is bounded by exactly $k$ edges.

Write down the minimum number of edges in $G$ .

[1]

a.i.

Find the maximum number of edges in $G$ .

[2]

a.ii.

Find the maximum number of edges in $G$ , given that $G$ contains an Eulerian circuit.

[2]

a.iii.

Explain why $2e = kf$ .

[2]

b.i.

Find the value of $f$ when $v = 9$ and $k = 3$ .

[3]

b.ii.

Find the possible values of $f$ when $v = 13$ .

[4]

b.iii.

A driver needs to make deliveries to five shops $A$ , $B$ , $C$ , $D$ and $E$ . The driver starts and finishes his journey at the warehouse $W$ . The driver wants to find the shortest route to visit all the shops and return to the warehouse. The distances, in kilometres, between the locations are given in the following table.

By deleting $W$ , use the deleted vertex algorithm to find a lower bound for the length of a route that visits every shop, starting and finishing at $W$ .

[6]

Starting from $W$ , use the nearest-neighbour algorithm to find a route which gives an upper bound for this problem and calculate its length.

[4]