Find the maximum possible value of $e$.

Find an expression for $e\text{'}$ in terms of $e$.

Given that the complement of $G$ is also planar and connected, find the possible values of $e$.

$H$ is a simple graph with $v$ vertices and $e$ edges.

Given that both $H$ and its complement are planar and connected, find the maximum possible value of $v$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

substitutes  $v=9$  into either  $e=3v-6$  or  $e\le 3v-6$        (M1)

the maximum number of edges is  $21 \left(e\le 21\right)$        A1

[2 marks]

${\kappa }_9$ has $\left(\left(\begin{array}{c}9\\ 2\end{array}\right)=\right) 36 \text{edges}$        (A1)

so  $e\text{'}=36-e \left(=\left(\begin{array}{c}9\\ 2\end{array}\right)-e\right)$        A1

[2 marks]

$e\text{'}\le 21\Rightarrow 36-e\le 21$        (M1)

$15\le e\le 21$  (the possible values are $15, 16, 17, 18, 19, 20$ and $21$)        A1

[2 marks]

recognises that $e+e\text{'}=\frac{v\left(v-1\right)}{2}$ (or equivalent)        (A1)

uses  $e\le 3v-6$  and  $e\text{'}\le 3v-6$        M1

to form $\frac{v\left(v-1\right)}{2}-\left(3v-6\right)\le 3v-6$        A1

Note: Award A1 for $\frac{v\left(v-1\right)}{2}-\left(3v-6\right)=3v-6$.

attempts to solve their quadratic inequality (equality)        (M1)

$v^2-13v+24\le 0\Rightarrow 2.228\dots \le v\le 10.77\dots$

the maximum possible value of $v$ is $10 \left(v\le 10\right)$        A1

[5 marks]

Use Dijkstra’s algorithm to find the shortest time to travel from $\text{C}$ to $\text{F}$, clearly showing how the algorithm has been applied.

Hence write down the shortest path from $\text{C}$ to $\text{F}$.

A new road is constructed that allows Christine to travel from $\text{H}$ to $\text{A}$ in $t$ minutes. If Christine starts from home and uses this new road her minimum travel time to $\text{A}$ is reduced, but her minimum travel time to $\text{F}$ remains the same.

Find the possible values of $t$.

attempts to construct a graph or table to represent Dijkstra’s algorithm       M1

EITHER

OR

a clear attempt at Step 1 ($\text{C,\hspace{0.05em}D,\hspace{0.05em}H}$ and $\text{B}$ considered)        M1

Steps 2 and 3 correctly completed        A1

Step 4 ($\text{A\hspace{0.05em}}: 44\to 36$) correctly completed        A1

Steps 5 and 6 ($\text{E\hspace{0.05em}}: 41\to 40$  and  $\text{F\hspace{0.05em}}: 58\to 57$  or  $57\to 55$  or  $58\to 55$) correctly completed        A1

shortest time $=55$  (mins)        A1

[6 marks]

$\text{CHGEF}$        A1

Note: Award A1 only if it is clear that Dijkstra’s algorithm has been attempted in part (a) (i). This A1 can be awarded if the candidate attempts to use Dijkstra’s algorithm but neglects to state $55$ (mins).

[1 mark]

minimum travel time from $\text{C}$ to $\text{A}$ is reduced

$\text{CHA}$ is now $12+t$  (mins)        (M1)

$\text{CBA}$ is still $25+11$  (mins)

so $12+t<36 \left(t<24\right)$        (A1)

Note: Condone $t\le 24$.

travel time from $\text{C}$ to $\text{F}$ remains the same ($55$ mins)

$\text{CHAF}$ is now $12+t+21$  (mins)        (M1)

$12+t+21\ge 55 \left(t\ge 22\right)$        (A1)

so $22\le t<24$         A1

Note: Accept $t=22, 23$.

[5 marks]

Write down a Hamiltonian cycle in $W$.

Use Prim’s algorithm, starting at vertex $\text{B}$, to find the weight of the minimum spanning tree of the remaining graph. You should indicate clearly the order in which the algorithm selects each edge.

Hence, for the case where $x<9$, find a lower bound for Daniel’s travel time, in terms of $x$.

$p$.

$q$.

$r$.

Use the nearest neighbour algorithm to find two possible cycles.

Find the best upper bound for Daniel’s travel time.

Find the least value of $x$ for which the edge $\text{AF}$ will definitely not be used by Daniel.

Hence state the value of the upper bound for Daniel’s travel time for the value of $x$ found in part (e)(i).

The tourist office in the city has received complaints about the lack of cleanliness of some routes between the attractions. Corinne, the office manager, decides to inspect all the routes between all the attractions, starting and finishing at $\text{H}$. The sum of the weights of all the edges in graph $W$ is $(92+x)$.

Corinne inspects all the routes as quickly as possible and takes $2$ hours.

Find the value of $x$ during Corinne’s inspection.

e.g. $\text{ABCDEGHFA}$            A1

Note: Accept any other correct answers starting at any vertex.

[1 mark]

$7$ vertices, so $6$ edges required for MST                       (M1)

Note: To award (M1), their $6$ edges should not form a cycle.

            M1A1A1

Note: Award M1 for the first three edges in correct order, A1 for $\text{BH}$ in correct order and A1 for all of the edges correct.

weight of MST $=33$            A1

Note: The final A1 can be awarded independently of previous marks.

[5 marks]

lower bound $=33+3+x$                      (M1)

$=36+x$            A1

[2 marks]

$p=13$           A1

[1 mark]

$q=17$           A1

[1 mark]

$r=14$           A1

[1 mark]

attempt to use nearest neighbour algorithm                      (M1)

any two correct cycles from
$\text{ABCDEGHFA, AFGHBCDE(F)A, AB(A)FGHCDE(F)A}$           A1A1

Note: Bracketed vertices may be omitted in candidate’s answer.
Award M1A0A1 for candidates who list two correct sequences of vertices, but omit the final vertex $\text{A}$.

[3 marks]

use $\text{ABCDEGHFA}$  OR  their shortest cycle from (d)(i)                   (M1)

upper bound $=43$           A1

[2 marks]

cycle starts: $\text{ABCDEGHF}$

return to $\text{A}$ has two options, $\text{FA}=18$ or $x$                   (M1)

hence least value of $x=19$           A1

[2 marks]

upper bound $=58$           A2

[2 marks]

recognition that edges will be repeated / there are odd vertices           (M1)

$\text{BH}+\text{DG}=21, \text{BD}+\text{GH}=15, \text{BG}+\text{DH}=21$  OR  $18+x$           A1

recognizing $\text{BD}$ and $\text{GH}$ is lowest weight and is repeated           (M1)

solution to CPP $=107+x$           A1

$x=13$           A1

Note: Award M1A0M0A1A1 if only pairing $\text{BD}$ and $\text{GH}$ is considered, leading to a correct answer.

[5 marks]

Mostly well done, although some candidates wrote down a path instead of a cycle and some candidates wrote a cycle that did not include all the vertices.

Many candidates could apply the algorithm correctly to find the weight of the minimum spanning tree. A common misconception was selecting the shortest edge adjacent to the previous vertex, instead of selecting the shortest edge adjacent to the existing tree. This approach will not necessarily find the minimum spanning tree. A small number of candidates found the correct minimum spanning tree, but did not show evidence of using Prim’s algorithm, which only received partial credit; where a method/algorithm is explicit in the question, working must be seen to demonstrate that approach. Part (b)(ii) was also answered reasonably well, however several candidates did not read the instruction to give their answer in terms of $\mathrm{x}$, instead choosing a specific value.

Many candidates could apply the algorithm correctly to find the weight of the minimum spanning tree. A common misconception was selecting the shortest edge adjacent to the previous vertex, instead of selecting the shortest edge adjacent to the existing tree. This approach will not necessarily find the minimum spanning tree. A small number of candidates found the correct minimum spanning tree, but did not show evidence of using Prim’s algorithm, which only received partial credit; where a method/algorithm is explicit in the question, working must be seen to demonstrate that approach. Part (b)(ii) was also answered reasonably well, however several candidates did not read the instruction to give their answer in terms of $\mathrm{x}$, instead choosing a specific value.

Mostly well-answered.

Mostly well-answered.

Mostly well-answered.

Many candidates could successfully apply the nearest neighbour algorithm to find a correct cycle, but some made errors finding a second one. Part (ii) was done reasonably well, with many candidates either giving the correct answer or gaining follow-through marks for selecting their shortest cycle from part (d)(i). A small number of candidates incorrectly chose their longest cycle.

Many candidates could successfully apply the nearest neighbour algorithm to find a correct cycle, but some made errors finding a second one. Part (ii) was done reasonably well, with many candidates either giving the correct answer or gaining follow-through marks for selecting their shortest cycle from part (d)(i). A small number of candidates incorrectly chose their longest cycle.

This question had a mixed response. Some candidates used the table or the graph to realize that the two choices to get from $\mathrm{A}$ to $\mathrm{F}$ are either $18$ or $\mathrm{x}$. Some incorrectly stated $\mathrm{x}=18$. These candidates often achieved success in part (e)(ii), making the connection to their previous answer in part (d).

This question had a mixed response. Some candidates used the table or the graph to realize that the two choices to get from $\mathrm{A}$ to $\mathrm{F}$ are either $18$ or $\mathrm{x}$. Some incorrectly stated $\mathrm{x}=18$. These candidates often achieved success in part (e)(ii), making the connection to their previous answer in part (d).

A surprising number of candidates did not seem to realize this was an application of the Chinese Postman Problem and simply equated the given total weight to $120$ minutes. Not only does this show a lack of understanding of the problem, but it also showed a lack of appreciation of the amount of work required to answer a 5 mark question. Out of the many candidates who recognized the need to repeat edges connecting the odd vertices, some did not show complete working to explain why they chose to connect $\mathrm{BD}$ and $\mathrm{GH}$, only gaining partial credit.

Find an expression for the width of $U_n$ in centimetres.

Given the width of a pixel is approximately $0.025 \text{cm}$, find the number of squares in the final image.

Write down ${\mathit{A}}_1$.

Write down ${\mathit{A}}_n$, in terms of $n$.

state the coordinates, $\left(x_1, y_1\right)$, of its image in $U_1$.

hence find ${\mathit{b}}_1$.

show that ${\mathit{b}}_n=\left(\begin{array}{c}8\left(1-2^{-n}\right)\\ 8\left(1-2^{-n}\right)\end{array}\right)$.

Hence or otherwise, find the coordinates of the top left-hand corner in $U_7$.

Find, $s$, in the form $s\left(\theta \right)=m\theta +c$.

Write down $E_{\theta }$.

Hence find the image of $(1, 1)$ after it is rotated $135°$ and enlarged.

Find the value of $\theta$ at which the enlargement scale factor equals zero.

After the enlargement scale factor equals zero, Ben continues to rotate the image for another two revolutions.

Describe the animation for these two revolutions, stating the final position of the sequence of squares.

* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.

$4\left(\frac{1}{2^n}\right)$       M1A1

[2 marks]

$\frac{4}{2^n}>0.025$        (A1)

$2^n<160$

$n\le 7$        (A1)

Note: Accept equations in place of inequalities.  

Hence there are $8$ squares        A1

[3 marks]

$\left(\begin{array}{cc}\frac{1}{2}& 0\\ 0& \frac{1}{2}\end{array}\right)$        A1

[1 mark]

$A_n=\left(\begin{array}{cc}\frac{1}{2^n}& 0\\ 0& \frac{1}{2^n}\end{array}\right)$        A1

[1 mark]

$\left(4, 4\right)$        A1

[1 mark]

${\mathit{A}}_1\left(\begin{array}{c}0\\ 0\end{array}\right)+{\mathit{b}}_1=\left(\begin{array}{c}4\\ 4\end{array}\right)$        (M1)

 ${\mathit{b}}_1=\left(\begin{array}{c}4\\ 4\end{array}\right)$        A1

[2 marks]

Recognise the geometric series ${\mathit{b}}_n=\left(\begin{array}{c}4+2+1+\dots \\ 4+2+1+\dots \end{array}\right)$        M1

Each component is equal to $\frac{4\left(1-{\displaystyle \frac{1}{2^n}}\right)}{{\displaystyle \frac{1}{2}}} \left(=8\left(1-\frac{{\displaystyle 1}}{{\displaystyle 2^n}}\right)\right)$        M1A1

$\left(\begin{array}{c}8\left(1-\frac{1}{2^n}\right)\\ 8\left(1-\frac{1}{2^n}\right)\end{array}\right)$        AG

[3 marks]

$\left(\begin{array}{cc}\frac{1}{2^7}& 0\\ 0& \frac{1}{2^7}\end{array}\right)\left(\begin{array}{c}0\\ 4\end{array}\right)+\left(\begin{array}{c}8\left(1-\frac{1}{2^7}\right)\\ 8\left(1-\frac{1}{2^7}\right)\end{array}\right)$        M1A1

$\left(7.9375, 7.96875\right)$        A1

[3 marks]

$s\left(\theta \right)=m\theta +c$

$s\left(0\right)=1, c=1$        M1A1

$s\left(360\right)=\frac{1}{2}$        A1

$\frac{1}{2}=360m+1\Rightarrow m=-\frac{1}{720}$        A1

$s\left(\theta \right)=-\frac{\theta }{720}+1$

[4 marks]

$E_{\theta }=\left(\begin{array}{cc}-\frac{\theta }{720}+1& 0\\ 0& -\frac{\theta }{720}+1\end{array}\right)$        A1

[1 mark]

$\left(\begin{array}{cc}-\frac{135}{720}+1& 0\\ 0& -\frac{135}{720}+1\end{array}\right)\left(\begin{array}{cc}\cos 135°& -\sin 135°\\ \sin 135°& \cos 135°\end{array}\right)\left(\begin{array}{c}1\\ 1\end{array}\right)$        M1A1A1

 $\left(-1.15, 0\right)$        A1

[4 marks]

$\theta =720°$      A1

[1 mark]

The image will expand from zero (accept equivalent answers)

It will rotate counter clockwise

The design will (re)appear in the opposite (third) quadrant         A1A1

Note: Accept any two of the above

Its final position will be in the opposite (third) quadrant or $180˚$ from its original position or equivalent statement.         A1

[3 marks]

The model assumes that each town is positioned at a single point. Describe possible circumstances in which this modelling assumption is reasonable.

Sketch a Voronoi diagram showing the regions within the metropolitan area that are closest to each town.

Find the equation of the perpendicular bisector of $\left[\text{IF}\right]$.

Given that the coordinates of one vertex of the new Voronoi diagram are $(20, 37.5)$, find the coordinates of the other two vertices within the metropolitan area.

Sketch this new Voronoi diagram showing the regions within the metropolitan area which are closest to each town.

A car departs from a point due north of Hamilton. It travels due east at constant speed to a destination point due North of Gaussville. It passes through the Edison, Isaacopolis and Fermitown districts. The car spends $30\%$ of the travel time in the Isaacopolis district.

Find the distance between Gaussville and the car’s destination point.

Find the location of the toxic waste dump, given that this location is not on the edge of the metropolitan area.

Make one possible criticism of the council’s choice of location.

Find which town is last to be polluted. Justify your answer.

Write down the number of days it takes for the pollution to reach the last town.

A sewer inspector needs to plan the shortest possible route through each of the connections between different locations. Determine an appropriate start point and an appropriate end point of the inspection route.

Note that the fact that each location is connected to itself does not correspond to a sewer that needs to be inspected.

the size of each town is small (in comparison with the distance between the towns)
OR
if towns have an identifiable centre
OR
the centre of the town is at that point       R1

Note: Accept a geographical landmark in place of “centre”, e.g. “town hall” or “capitol”.

[1 mark]

       A1

Note: There is no need for a scale / coordinates here. Condone boundaries extending beyond the metropolitan area.

[1 mark]

the gradient of $\text{IF}$ is $\frac{40-20}{40-30}=2$          (A1)

negative reciprocal of any gradient          (M1)

gradient of perpendicular bisector $=\frac{1}{2}$

Note: Seeing $-\frac{2}{3}$ (for example) used clearly as a gradient anywhere is evidence of the “negative reciprocal” method despite being applied to an inappropriate gradient.

midpoint is $\left(\frac{40+30}{2}, \frac{40+20}{2}\right)=\left(35, 30\right)$          (A1)

equation of perpendicular bisector is $y-30=-\frac{1}{2}\left(x-35\right)$         A1

Note: Accept equivalent forms e.g. $y=-\frac{1}{2}x+\frac{95}{2}$  or  $2y+x-95=0$.
Allow FT for the final A1 from their midpoint and gradient of perpendicular bisector, as long as the M1 has been awarded

[4 marks]

the perpendicular bisector of $\text{EH}$ is $y=20$          (A1)

Note: Award this A1 if seen in the $y$-coordinate of any final answer or if $20$ is used as the $y$-value in the equation of any other perpendicular bisector.

attempt to use symmetry OR intersecting two perpendicular bisectors         (M1)

$\left(\frac{25}{3}, 20\right)$         A1

$\left(20, 2.5\right)$         A1

[4 marks]

         M1A1

Note: Award M1 for exactly four perpendicular bisectors around $\text{I}$ ($\text{IE}$, $\text{IF}$, $\text{IG}$ and $\text{IH}$) seen, even if not in exactly the right place.

Award A1 for a completely correct diagram. Scale / coordinates are NOT necessary. Vertices should be in approximately the correct positions but only penalized if clearly wrong (condone northern and southern vertices appearing to be very close to the boundary).

Condone the Voronoi diagram extending outside of the square.

Do not award follow-though marks in this part.

[2 marks]

$30\%$ of $40$ is $12$         (A1)

recognizing line intersects bisectors at $y=c$ (or equivalent) but different $x$-values          (M1)

$c=\frac{3}{2}{x}_1+\frac{15}{2}$  and $c=-\frac{1}{2}{x}_2+\frac{95}{2}$

finding an expression for the distance in Isaacopolis in terms of one variable         (M1)

$x_2-x_1=\left(95-2c\right)-\frac{2c-15}{3}=100-\frac{8c}{3}$

equating their expression to $12$

$100-\frac{8c}{3}=0.3\times 40=12$

$c=33$

distance $=33 \left(\text{km}\right)$        A1

[4 marks]

must be a vertex (award if vertex given as a final answer)         (R1)

attempt to calculate the distance of at least one town from a vertex         (M1)

Note: This must be seen as a calculation or a value.

correct calculation of distances        A1

$\frac{65}{3}$  OR  $21.7$  AND  $\sqrt{406.25}$  OR  $20.2$

$\left(\frac{25}{3}, 20\right)$        A1

Note: Award R1M0A0A0 for a vertex written with no other supporting calculations.
Award R1M0A0A1 for correct vertex with no other supporting calculations.
The final A1 is not dependent on the previous A1. There is no follow-through for the final A1.

Do not accept an answer based on “uniqueness” in the question.

[4 marks]

For example, any one of the following:

decision does not take into account the different population densities

closer to a city will reduce travel time/help employees

it is closer to some cites than others        R1

Note: Accept any correct reason that engages with the scenario.
Do not accept any answer to do with ethical issues about whether toxic waste should ever be dumped, or dumped in a metropolitan area.

[1 mark]

METHOD 1

attempting ${\mathit{M}}^3$         M1

attempting ${\mathit{M}}^4$         M1

e.g.

last row/column of ${\mathit{M}}^3=\left(3 5 1 6 0 7\right)$

last row/column of ${\mathit{M}}^4=\left(10 12 4 16 1 18\right)$

hence Isaacopolis is the last city to be polluted          A1

Note: Do not award the A1 unless both ${\mathit{M}}^3$ and ${\mathit{M}}^4$ are considered.
Award M1M0A0 for a claim that the shortest distance is from $T$ to $I$ and that it is $4$, without any support.

METHOD 2

attempting to translate $\mathit{M}$ to a graph or a list of cities polluted on each day         (M1)

correct graph or list         A1

hence Isaacopolis is the last city to be polluted          A1

Note: Award M1A1A1 for a clear description of the graph in words leading to the correct answer.

[3 marks]

it takes $4$ days        A1

[1 mark]

EITHER

the orders of the different vertices are:

$\text{E 2}$
$\text{F 1}$
$\text{G 2}$
$\text{H 2}$
$\text{I \hspace{0.05em}\hspace{0.05em}\hspace{0.05em}1}$
$\text{T 2}$           (A1)

Note: Accept a list where each order is $2$ greater than listed above.

OR

a correct diagram/graph showing the connections between the locations           (A1)

Note: Accept a diagram with loops at each vertex.
This mark should be awarded if candidate is clearly using their correct diagram from the previous part.

THEN

“Start at F and end at I”  OR  “Start at I and end at F”            A1

Note: Award A1A0 for “it could start at either F or I”.
Award A1A1 for “IGEHTF” OR “FTHEGI”.
Award A1A1 for “F and I” OR “I and F”.

[2 marks]

Question 2 was based on Voronoi diagrams, but a substantial number of candidates appeared to have not met this topic.

2(a) was generally well answered, although a strangely common answer was to claim that the towns must be 1km by 1km! Perhaps this came from thinking of coordinates as representing pixels rather than points.

2(b) was done well by most candidates who knew what a Voronoi diagram was.

2(c)(i) showed some poor planning skills by many candidates who found a line perpendicular to the given Voronoi edge rather than finding the gradient of IF.

In 2(c)(ii) candidates would have benefited from taking a step back and thinking about the symmetry of the situation before unthinkingly intersecting a lot of lines.

2(c)(iii) was done well by some, but many did not seem to have any intuition for the effect of adding a point to a Voronoi diagram.

2(d) was probably the worst answered question. Candidates did not seem to have the problem-solving tools to deal with this slightly unfamiliar situation.

In 2(e) many candidates clearly did not know that the solution to the toxic waste problem (as described in the syllabus) occurs at a vertex of the Voronoi diagram.

A pleasing number of candidates were able to approach 2(f) even if they were unable to do earlier parts of the question, and in these very long questions candidates should be advised that sometimes later parts are not necessarily harder or impossible to access. Very few who attempted the matrix power approach could interpret what zeroes meant in the matrices produced, but a good number successfully turned the matrix into a graph and proceeded well from there.

Find $\text{AF}$.

Find the cost per metre of installing this cable.

State why the cost for installing the cable between $\text{A}$ and $\text{F}$ would be higher than between the other buildings.

By using Kruskal’s algorithm, find the minimum spanning tree for $S$, showing clearly the order in which edges are added.

Hence find the minimum installation cost for the cables that would allow all the buildings to be part of the computer network.

State why a path that forms a Hamiltonian cycle does not always form an Eulerian circuit.

Starting at $\text{D}$, use the nearest neighbour algorithm to find the upper bound for the installation cost of a computer network in the form of a Hamiltonian cycle.

Note: Although the graph is not complete, in this instance it is not necessary to form a table of least distances.

By deleting $\text{D}$, use the deleted vertex algorithm to find the lower bound for the installation cost of the cycle.

Show that Jonas’s network satisfies the requirement of there being less than a $2\%$ probability of the network failing after a power surge.

${\text{AF}}^2=89.2^2+104.9^2-2\left(89.2\right)\left(104.9\right)\cos 83$         (M1)(A1)

Note: Award (M1) for substitution into the cosine rule and (A1) for correct substitution.

$\text{AF}=129 \text{m} \left(129.150\dots \right)$           A1

[3 marks]

$21310÷129.150\dots$         (M1)

$\$165$           A1

[2 marks]

any reasonable statement referring to the lake         R1

(eg. there is a lake between $\text{A}$ and $\text{F}$, the cables would need to be installed under/over/around the lake, special waterproof cables are needed for lake, etc.)

[1 mark]

edges (or weights) are chosen in the order

$\text{CE} \left(8239\right)$
$\text{DG} \left(8668\right)$
$\text{BD } \left(8778\right)$
$\text{AB} \left(8811\right)$
$\text{DE } \left(8833\right)$
$\text{EH} \left(9251\right)$
$\text{DF} \left(11 539\right)$               A1A1A1

Note: Award A1 for the first two edges chosen in the correct order. Award A1A1 for the first six edges chosen in the correct order. Award A1A1A1 for all seven edges chosen in the correct order. Accept a diagram as an answer, provided the order of edges is communicated.

[3 marks]

Finding the sum of the weights of their edges               (M1)
$8239+8668+8778+8811+8833+9251+11539$

total cost $=\$64119$               A1

[2 marks]

a Hamiltonian cycle is not always an Eulerian circuit as it does not have to include all edges of the graph (only all vertices)             R1

[1 mark]

edges (or weights) are chosen in the order

$\text{DG} \left(8668\right)$
$\text{GH} \left(9603\right)$
$\text{HE} \left(9251\right)$
$\text{EC} \left(8239\right)$
$\text{CB} \left(13 156\right)$
$\text{BA} \left(8811\right)$
$\text{AF} \left(21 310\right)$
$\text{FD} \left(11 539\right)$              A1A1A1

Note: Award A1 for the first two edges chosen in the correct order. Award A1A1 for the first five edges chosen in the correct order. Award A1A1A1 for all eight edges chosen in the correct order. Accept a diagram as an answer, provided the order of edges is communicated.

finding the sum of the weights of their edges                (M1)
$8668+9603+9251+8239+13156+8811+21310+11539$

upper bound $=\$90 577$              A1

[5 marks]

attempt to find MST after deleting vertex D         (M1)
these edges (or weights) (in any order)

$\text{CE} \left(8239\right)$
$\text{AB} \left(8811\right)$
$\text{EH} \left(9251\right)$
$\text{GH} \left(9603\right)$
$\text{BE} \left(10 153\right)$
$\text{FG} \left(12 606\right)$              A1

Note: Prim’s or Kruskal’s algorithm could be used at this stage.

reconnect $\text{D}$ to MST with two different edges         (M1)

$\text{DG} \left(8668\right)$
$\text{BD} \left(8778\right)$              A1

Note: This A1 is independent of the first A mark and can be awarded if both $\text{DG}$ and $\text{BD}$ are chosen to reconnect $\text{D}$ to the MST, even if the MST is incorrect.

finding the sum of the weights of their edges              (M1)
$8239+8811+9251+9603+10153+12606+8668+8778$

Note: For candidates with an incorrect MST or no MST, the weights of at least seven of the edges being summed (two of which must connect to $\text{D}$) must be shown to award this (M1).

lower bound $=\$76 109$              A1

[6 marks]

METHOD 1

recognition of a binomial distribution         (M1)
$X~\text{B}\left(2, 0.014\right)$

finding the probability that a cable fails (at least one of its connections fails)
$\text{P}\left(X>0\right)=0.027804$  OR  $1-\text{P}\left(X=0\right)=0.027804$             A1

recognition that two cables must fail for the network to go offline         M1

recognition of binomial distribution for network, $Y~\text{B}\left(8, 0.027804\right)$         (M1)

$\text{P}\left(Y\ge 2\right)=0.0194 \left(0.0193602\dots \right)$  OR  $1-\text{P}\left(Y<2\right)=0.0194 \left(0.0193602\dots \right)$             A1

therefore, the diagram satisfies the requirement since $1.94\%<2\%$             AG

Note: Evidence of binomial distribution may be seen as combinations.

METHOD 2

recognition of a binomial distribution          (M1)
$X~\text{B}\left(16, 0.014\right)$

finding the probability that at least two connections fail
$\text{P}\left(X\ge 2\right)=0.0206473\dots$  OR  $1-\text{P}\left(X<2\right)=0.0206473\dots$             A1

recognition that the previous answer is an overestimate          M1

finding probability of two ends of the same cable failing, $F~\text{B}\left(2, 0.014\right)$,
and the ends of the other $14$ cables not failing, $S~\text{B}\left(14, 0.014\right)$
$\text{P}\left(F=2\right)\times \text{P}\left(S=0\right)=0.0000160891\dots$             (A1)

$0.0000160891\dots \times 8=0.00128713...$

$0.0206473\dots -0.00128713\dots =0.0194 \left(0.0193602\dots \right)$             A1

therefore, the diagram satisfies the requirement since $1.94\%<2\%$             AG

METHOD 3

recognition of a binomial distribution          M1
$X~\text{B}\left(16, 0.014\right)$

finding the probability that the network remains secure if $0$ or $1$ connections fail or if $2$ connections fail provided that the second failed connection occurs at the other end of the cable with the first failure         (M1)

$\text{P}$(remains secure) $=\text{P}\left(X\le 1\right)+\frac{1}{15}\times \text{P}\left(X=2\right)$             A1

$=0.9806397625$             A1

$\text{P}$(network fails) $=1-0.9806397625=0.0194 \left(0.0193602\dots \right)$              A1

therefore, the diagram satisfies the requirement since $1.94\%<2\%$             AG

METHOD 4

$\text{P}$(network failing)

$=1-\text{P}\left(0 \text{connections failing}\right)-\text{P}\left(1 \text{connection failing}\right)-\text{P}\left(2 \text{connections on the same cable failing}\right)$          M1

$=1-0.{986}^{16}-{}_{16}C_1\times 0.014\times 0.{986}^{15}-{}_{8}C_1\times 0.{014}^2\times 0.{986}^{14}$              A1A1A1

Note: Award A1 for each of 2^nd, 3^rd and last terms.

$=0.0194 \left(0.0193602\dots \right)$              A1

therefore, the diagram satisfies the requirement since $1.94\%<2\%$             AG

[5 marks]

This question part was intended to be an easy introduction to help candidates begin working with the larger story and most candidates handled it well. However, it was surprisingly common for a candidate to correctly choose the cosine rule and to make the correct substitutions into the formula but then arrive at an incorrect answer. The frequency of this mistake suggests that candidates were either making simple entry mistakes into their GDC or forgetting to ensure that their GDC was set to degrees rather than radians.

(b) and (c) Most candidates were able to gain the three marks available.

(d), (f) and (g) These three question parts required candidates to demonstrate their ability to carry out graph theory algorithms. Kruskal’s algorithm was split into two different question parts to guide candidates to show their work. As a result, many were able to score well in part (d)(ii) either from having the correct MST or from “follow through” marks from an incorrect MST. However, without this guidance in 2(f) and 2(g), many candidates did a poor job of showing the process they were using to apply the algorithms. The candidates that scored well were detailed in showing the order of how edges were selected and how they were being summed to arrive at the final answers. Although “follow through” within the problem was not available for the final answer in parts 2(f) and 2(g), many candidates missed the opportunity to gain the final method mark in both parts by not fully showing the process they used.

Many candidates were able to state the definitions of Hamiltonian cycles and Eulerian circuits. However, the question was not asking for definitions but rather a distinct conclusion of why a Hamiltonian cycle is not always an Eulerian circuit. Disappointingly, many incorrect answers contained five or more lines or writing that may have used up exam time that could have been devoted to other question parts. Another common mistake seen here was candidates incorrectly trying to state a reason based on the number of odd vertices.

This question was very challenging for almost all the candidates. Although there were several different methods that candidates could have used to answer this question, most candidates were only able to gain one or two marks here. Many candidates did recognize that something binomial was needed, but few knew how to setup the correct parameters for the distribution.

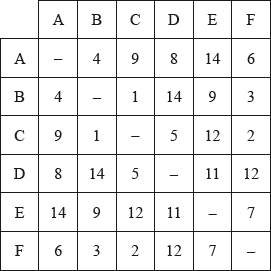
Starting at A , use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for $G$.

By first deleting vertex A , use the deleted vertex algorithm together with Kruskal’s algorithm to find a lower bound for the travelling salesman problem for $G$.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

the edges are traversed in the following order

AB     A1

BC

CF     A1

FE

ED     A1

DA   A1

$\text{upper bound}=\text{weight of this cycle}=4+1+2+7+11+8=33$     A1

[5 marks]

having deleted A, the order in which the edges are added is

BC     A1

CF     A1

CD     A1

EF     A1

Note:     Accept indication of the correct order on a diagram.

to find the lower bound, we now reconnect A using the two edges with the lowest weights, that is AB and AF     (M1)(A1)

$\text{lower bound}=1+2+5+7+4+6=25$     A1

Note:     Award (M1)(A1)A1 for $\text{LB}=15+4+6=25$ obtained either from an incorrect order of correct edges or where order is not indicated.

[7 marks]

State, with a reason, whether or not G has an Eulerian circuit.

Use Kruskal’s algorithm to find a minimum spanning tree for G, stating its total weight. Indicate clearly the order in which the edges are added.

Use a suitable algorithm to show that the minimum time in which Mr José can get from A to E is 13 minutes.

Find the minimum time it takes Mr José to patrol the resort if he has to walk along every road at least once, starting and ending at A. State clearly which roads need to be repeated.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

no because the graph has vertices (A, B, D, F) of odd degree        R1

[1 mark]

the edges are added in the order

BI   5  

DH   5       A1

AB   6  

AF   6  

CI   6       A1

CD   7  

EF   7       A1

total weight = 42           A1

Note: The orders of the edges with the same weight are interchangeable.
Accept indication of correct edge order on a diagram.

[4 marks]

clear indication of using Dijkstra for example       M1

[5 marks]

there are 4 vertices of odd degree (A, F, B and D)       (A1)

attempting to list at least 2 possible pairings of odd vertices       M1

A → F and B → D has minimum weight 6 + 17 = 23

A → B and F → D has minimum weight 6 + 18 = 24

A → D and F → B has minimum weight 20 + 12 = 32       A1A1

Note: Award A1A0 for 2 pairs.

minimum time is (116 + 23 =) 139 (mins)       (M1)A1

roads repeated are AF, BC and CD       A1

[7 marks]

In the context of graph theory, explain briefly what is meant by a circuit;

In the context of graph theory, explain briefly what is meant by an Eulerian circuit.

The graph $G$ has six vertices and an Eulerian circuit. Determine whether or not its complement $G^{\prime }$ can have an Eulerian circuit.

Find an example of a graph $H$, with five vertices, such that $H$ and its complement $H^{\prime }$ both have an Eulerian trail but neither has an Eulerian circuit. Draw $H$ and $H^{\prime }$ as your solution.

a circuit is a walk that begins and ends at the same vertex and has no repeated edges     A1

[1 mark]

an Eulerian circuit is a circuit that contains every edge of a graph     A1

[1 mark]

if $G$ has an Eulerian circuit all vertices are even (are of degree 2 or 4)     A1

hence, $G^{\prime }$ must have all vertices odd (of degree 1 or 3)     R1

hence, $G^{\prime }$ cannot have an Eulerian circuit     R1

Note:     Award A1 to candidates who begin by considering a specific $G$ and $G^{\prime }$ (diagram). Award R1R1 to candidates who then consider a general $G$ and $G^{\prime }$.

[3 marks]

for example

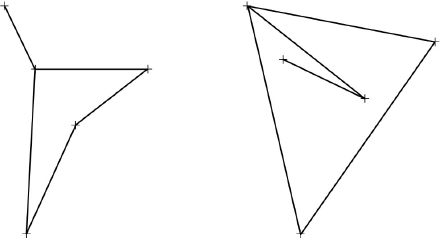
A2

A2

Notes:     Each graph must have 3 vertices of order 2 and 2 odd vertices. Award A2 if one of the graphs satisfies that and the final A2 if the other graph is its complement.

[4 marks]

State what feature of G ensures that G has an Eulerian trail.

State what feature of G ensures that G does not have an Eulerian circuit.

Write down an Eulerian trail in G.

Starting and finishing at B, find a solution to the Chinese postman problem for G.

Calculate the total weight of the solution.

G has an Eulerian trail because it has (exactly) two vertices (B and F) of odd degree      R1

[1 mark]

G does not have an Eulerian circuit because not all vertices are of even degree      R1

[1 mark]

for example BAEBCEFCDF      A1A1

Note: Award A1 for start/finish at B/F, A1 for the middle vertices.

[2 marks]

we require the Eulerian trail in (b), (weight = 65)     (M1)

and the minimum walk FEB (15)     A1

for example BAEBCEFCDFEB    A1

Note: Accept EB added to the end or FE added to the start of their answer in (b) in particular for follow through.

[3 marks]

total weight is (65 + 15=)80      A1

[1 mark]

Draw the weighted graph $H$.

Starting at library D use the nearest-neighbour algorithm, to find an upper bound for Mathilde’s minimum travelling distance. Indicate clearly the order in which the edges are selected.

By first removing library C, use the deleted vertex algorithm, to find a lower bound for Mathilde’s minimum travelling distance.

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

complete graph on 5 vertices     A1

weights correctly marked on graph     A1

[2 marks]

clear indication that the nearest-neighbour algorithm has been applied     M1

DA (or 16)     A1

AB (or 18) then BC (or 15)     A1

CE (or 17) then ED (or 19)     A1

$\text{UB}=85$     A1

[5 marks]

an attempt to find the minimum spanning tree     (M1)

DA (16) then BE (17) then AB (18) (total 51)     A1

reconnect C with the two edges of least weight, namely CB (15) and CE (17)     M1

$\text{LB}=83$     A1

[4 marks]

(i)     Draw the graph ${\kappa }_4$ including the weights of all the edges.

(ii)     Use the nearest-neighbour algorithm, starting at vertex ${\text{A}}_1$, to find a Hamiltonian cycle.

(iii)     Hence, find an upper bound to the travelling salesman problem for this weighted graph.

Consider the graph ${\kappa }_5$. Use the deleted vertex algorithm, with ${\text{A}}_5$ as the deleted vertex, to find a lower bound to the travelling salesman problem for this weighted graph.

(i)     Use the nearest-neighbour algorithm, starting at vertex ${\text{A}}_1$, to find a Hamiltonian cycle.

(ii)    Hence find and simplify an expression in $n$, for an upper bound to the travelling salesman problem for this weighted graph.

By splitting the weight of the edge ${\text{A}}_i{\text{A}}_j$ into two parts or otherwise, show that all Hamiltonian cycles of ${\kappa }_n$ have the same total weight, equal to the answer found in (c)(ii).

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

(i)          A1A1

Note: A1 for the graph, A1 for the weights.

(ii)     cycle is ${\text{A}}_1{\text{A}}_2{\text{A}}_3{\text{A}}_4{\text{A}}_1$     A1

(iii)     upper bound is $3+5+7+5=20$     A1

[4 marks]

with ${\text{A}}_5$ deleted, (applying Kruskal’s Algorithm) the minimum spanning tree will consist of the edges ${\text{A}}_1{\text{A}}_2,{\text{A}}_1{\text{A}}_3\text{, }{\text{A}}_1{\text{A}}_4$, of weights 3, 4, 5     (M1)A1

the two edges of smallest weight from ${\text{A}}_5$ are ${\text{A}}_5{\text{A}}_1$ and ${\text{A}}_5{\text{A}}_2$ of weights 6 and 7     (M1)A1

so lower bound is $3+4+5+6+7=25$     A1

[5 marks]

(i)     starting at ${\text{A}}_1$ we go ${\text{A}}_2,{\text{A}}_3\dots {\text{A}}_n$

we now have to take ${\text{A}}_n{\text{A}}_1$

thus the cycle is ${\text{A}}_1{\text{A}}_2{\text{A}}_3\dots {\text{A}}_{n-1}{\text{A}}_n{\text{A}}_1$     A1A1

Note: Final A1 is for ${\text{A}}_n{\text{A}}_1$.

(ii)     smallest edge from ${\text{A}}_1$ is ${\text{A}}_1{\text{A}}_2$ of weight 3, smallest edge from ${\text{A}}_2$ (to a new vertex) is ${\text{A}}_2{\text{A}}_3$ of weight 5, smallest edge from ${\text{A}}_{n-1}$ (to a new vertex) is ${\text{A}}_{n-1}{\text{A}}_n$ of weight $2n-1$     (M1)

weight of ${\text{A}}_n{\text{A}}_1$ is $n+1$

weight is $3+5+7+\dots +(2n-1)+(n+1)$     A1

$=\frac{(n-1)}{2}(2n+2)+(n+1)$    M1A1

$=n(n+1)$ (which is an upper bound)     A1

Note: Follow through is not applicable.

[7 marks]

put a marker on each edge ${\text{A}}_i{\text{A}}_j$ so that $i$ of the weight belongs to vertex ${\text{A}}_i$ and $j$ of the weight belongs to vertex ${\text{A}}_j$     M1

the Hamiltonian cycle visits each vertex once and only once and for vertex ${\text{A}}_i$ there will be weight $i$ (belonging to vertex ${\text{A}}_i$) both going in and coming out     R1

so the total weight will be $\sum _{i=1}^{n}2i=2\frac{n}{2}(n+1)=n(n+1)$     A1AG

Note: Accept other methods for example induction.

[3 marks]

Write down the minimum number of edges in $G$.

Find the maximum number of edges in $G$.

Find the maximum number of edges in $G$, given that $G$ contains an Eulerian circuit.

Explain why $2e=kf$.

Find the value of $f$ when $v=9$ and $k=3$.

Find the possible values of $f$ when $v=13$.

7 (a tree)        A1

[1 mark]

$\frac{8\times 7}{2}\left(7+6+5+4+3+2+1\right)$  (a complete graph)        (M1)

$=28$        A1

[2 marks]

$\frac{8\times 6}{2}$ (since every vertex must be of degree 6)        (M1)

$=24$        A1

[2 marks]

counting the edges around every face gives $kf$ edges       A1

but as every edge is counted in 2 faces        R1

$\Rightarrow kf=2e$       AG

[2 marks]

using $v-e+f=2$ with $v=9$       M1

EITHER

substituting $2e=3f$  into  $2\left(9\right)-2e+2f=4$       (M1)

OR

substituting $e=\frac{3f}{2}$  into  $9-e+f=2$       (M1)

THEN

$18-f=4$

$f=14$       A1

[3 marks]

$2v-kf+2f=4$  (or equivalent)       M1

when $v=13$

$\left(k-2\right)f=22$  or  $\left(2-k\right)f=-22$       A1

EITHER

$\left(k-2\right)f=1\times 2\times 11$      M1

OR

substituting at least two of  $k=13\text{, }4\text{, }3$  into  $f=\frac{22}{k-2}$  (or equivalent)      M1

THEN

$f=2\text{, }11\text{, 22}$  (since $f>1$)       A1

[4 marks]

By deleting $W$, use the deleted vertex algorithm to find a lower bound for the length of a route that visits every shop, starting and finishing at $W$.

Starting from $W$, use the nearest-neighbour algorithm to find a route which gives an upper bound for this problem and calculate its length.

deleting $\text{W}$ and its adjacent edges, the minimal spanning tree is

   A1A1A1A1

Note: Award the A1’s for either the edges or their weights.

the minimum spanning tree has weight = 54

Note: Accept a correct drawing of the minimal spanning tree.

adding in the weights of 2 deleted edges of least weight $\text{WB}$ and $\text{WC}$       (M1)
lower bound = 54 + 36 + 39

= 129         A1

[6 marks]

attempt at the nearest-neighbour algorithm      M1

$\text{WB}$
$\text{BA}$
$\text{AD}$
$\text{DE}$
$\text{EC}$
$\text{CW}$         A1

Note: Award M1 for a route that begins with $\text{WB}$ and then $\text{BA}$.

upper bound = 36 + 11 + 15 + 12 + 22 + 39 = 135       (M1)A1

[4 marks]