
SL Paper 1
A triangular field is such that and , each measured correct to the nearest metre, and the angle at is equal to , measured correct to the nearest .
Calculate the maximum possible area of the field.
Markscheme
attempt to find any relevant maximum value (M1)
largest sides are and (A1)
smallest possible angle is (A1)
attempt to substitute into area of a triangle formula (M1)
A1
[5 marks]
Examiners report
Iron in the asteroid 16 Psyche is said to be valued at quadrillion euros , where one quadrillion .
James believes the asteroid is approximately spherical with radius . He uses this information to estimate its volume.
Write down the value of the iron in the form where .
Calculate James’s estimate of its volume, in .
The actual volume of the asteroid is found to be .
Find the percentage error in James’s estimate of the volume.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1)(A1) (C2)
Note: Award (A1) for , (A1) for . Award (A1)(A0) for .
Award (A0)(A0) for answers of the type .
[2 marks]
(M1)
Note: Award (M1) for correct substitution in volume of sphere formula.
(A1) (C2)
[2 marks]
(M1)
Note: Award (M1) for their correct substitution into the percentage error formula (accept a consistent absence of “” from all terms).
(A1)(ft) (C2)
Note: Follow through from their answer to part (b). If the final answer is negative, award at most (M1)(A0).
[2 marks]
Examiners report
Three towns, , and are represented as coordinates on a map, where the and axes represent the distances east and north of an origin, respectively, measured in kilometres.
Town is located at and town is located at . A road runs along the perpendicular bisector of . This information is shown in the following diagram.
Find the equation of the line that the road follows.
Town is due north of town and the road passes through town .
Find the -coordinate of town .
Markscheme
midpoint A1
(M1)A1
Note: Accept equivalent gradient statements including using midpoint.
M1
Note: Award M1 for finding the negative reciprocal of their gradient.
OR OR A1
[5 marks]
substituting into their equation from part (a) (M1)
A1
Note: Award M1A0 for as their final answer.
[2 marks]
Examiners report
A large proportion of candidates seemed to be well drilled into finding the gradient of a line and the subsequent gradient of the normal. But without finding the coordinates of the midpoint of AB, no more marks were gained.
Many candidates worked out the value of correctly (or “correct” following the value they found in part (a)) but then incorrectly gave their answer as a coordinate pair.
The diagram below shows a helicopter hovering at point , vertically above a lake. Point is the point on the surface of the lake, directly below the helicopter.
Minta is swimming at a constant speed in the direction of point . Minta observes the helicopter from point as she looks upward at an angle of . After minutes, Minta is at point and she observes the same helicopter at an angle of .
Write down the size of the angle of depression from to .
Find the distance from to .
Find the distance from to .
Find Minta’s speed, in metres per hour.
Markscheme
A1
[1 mark]
OR OR (M1)
A1
[2 marks]
METHOD 1
attempt to find (M1)
(A1)
A1
METHOD 2
attempt to find (M1)
(A1)
A1
[3 marks]
A1
[1 mark]
Examiners report
The Voronoi diagram below shows three identical cellular phone towers, and . A fourth identical cellular phone tower, is located in the shaded region. The dashed lines in the diagram below represent the edges in the Voronoi diagram.
Horizontal scale: unit represents .
Vertical scale: unit represents .
Tim stands inside the shaded region.
Tower has coordinates and the edge connecting vertices and has equation .
Explain why Tim will receive the strongest signal from tower .
Write down the coordinates of tower .
Tower has coordinates .
Find the gradient of the edge of the Voronoi diagram between towers and .
Markscheme
every point in the shaded region is closer to tower R1
Note: Specific reference must be made to the closeness of tower .
[1 mark]
A1A1
Note: Award A1 for each correct coordinate. Award at most A0A1 if parentheses are missing.
[2 marks]
correct use of gradient formula (M1)
e.g.
taking negative reciprocal of their (at any point) (M1)
edge gradient A1
[3 marks]
Examiners report
Points and have coordinates and respectively.
The line , which passes through , has equation .
Express in terms of .
Find the value of .
Consider a unit vector , such that , where .
Point is such that .
Find the coordinates of .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
valid approach to find (M1)
eg
A1 N2
[2 marks]
valid approach (M1)
eg
one correct equation (A1)
eg
correct value for A1
eg
substituting their value into their expression/equation to find (M1)
eg
A1 N3
[5 marks]
valid approach (M1)
eg
correct working to find (A1)
eg and
correct approach to find (seen anywhere) A1
eg
recognizing unit vector has magnitude of (M1)
eg
correct working (A1)
eg
A1
substituting their value of (M1)
eg
(accept ) A1 N4
Note: The marks for finding are independent of the first two marks.
For example, it is possible to award marks such as (M0)(A0)A1(M1)(A1)A1 (M0)A0 or (M0)(A0)A1(M1)(A0)A0 (M1)A0.
[8 marks]
Examiners report
A piece of candy is made in the shape of a solid hemisphere. The radius of the hemisphere is .
Calculate the total surface area of one piece of candy.
The total surface of the candy is coated in chocolate. It is known that gram of the chocolate covers an area of .
Calculate the weight of chocolate required to coat one piece of candy.
Markscheme
OR (M1)(A1)(M1)
Note: Award M1 for use of surface area of a sphere formula (or curved surface area of a hemisphere), A1 for substituting correct values into hemisphere formula, M1 for adding the area of the circle.
A1
[4 marks]
(M1)
A1
[2 marks]
Examiners report
In this question, all lengths are in metres and time is in seconds.
Consider two particles, and , which start to move at the same time.
Particle moves in a straight line such that its displacement from a fixed-point is given by , for .
Find an expression for the velocity of at time .
Particle also moves in a straight line. The position of is given by .
The speed of is greater than the speed of when .
Find the value of .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
recognizing velocity is derivative of displacement (M1)
eg
velocity A1 N2
[2 marks]
valid approach to find speed of (M1)
eg , velocity
correct speed (A1)
eg
recognizing relationship between speed and velocity (may be seen in inequality/equation) R1
eg , speed = | velocity | , graph of speed , speed velocity
correct inequality or equation that compares speed or velocity (accept any variable for ) A1
eg
(seconds) (accept , do not accept ) A1 N2
Note: Do not award the last two A1 marks without the R1.
[5 marks]
Examiners report
A farmer owns a triangular field . The length of side is and side is . The angle between these two sides is .
Find the area of the field.
The farmer would like to divide the field into two equal parts by constructing a straight fence from to a point on .
Find . Fully justify any assumptions you make.
Markscheme
* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.
Area (M1)(A1)
A1
Note: units must be given for the final A1 to be awarded.
[3 marks]
(M1)A1
A1
METHOD 1
Because the height and area of each triangle are equal they must have the same length base R1
must be placed half-way along A1
A1
Note: the final two marks are dependent on the R1 being awarded.
METHOD 2
Let
M1
Use of area formula
A1
A1
[6 marks]
Examiners report
The following diagram shows a triangle .
, and .
Let .
Given that is acute, find .
Find .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
METHOD 1 – (sine rule)
evidence of choosing sine rule (M1)
eg
correct substitution (A1)
eg
A1 N2
METHOD 2 – (perpendicular from vertex )
valid approach to find perpendicular length (may be seen on diagram) (M1)
eg ,
correct perpendicular length (A1)
eg
A1 N2
Note: Do not award the final A mark if candidate goes on to state , as this demonstrates a lack of understanding.
[3 marks]
attempt to substitute into double-angle formula for cosine (M1)
correct working (A1)
eg
A1 N2
[3 marks]
Examiners report
A storage container consists of a box of length , width and height , and a lid in the shape of a half-cylinder, as shown in the diagram. The lid fits the top of the box exactly. The total exterior surface of the storage container is to be painted.
Find the area to be painted.
Markscheme
AND (A1)
(A1)
(A1)
(M1)
use of curved surface area formula (M1)
(A1)
A1
[7 marks]
Examiners report
Joey is making a party hat in the form of a cone. The hat is made from a sector, , of a circular piece of paper with a radius of and as shown in the diagram.
To make the hat, sides and are joined together. The hat has a base radius of .
Write down the perimeter of the base of the hat in terms of .
Find the value of .
Find the surface area of the outside of the hat.
Markscheme
A1
Note: Answer must be in terms of .
[1 mark]
METHOD 1
OR (M1)
Note: Award (M1) for correct substitution into length of an arc formula.
A1
METHOD 2
(M1)
A1
[2 marks]
EITHER
(M1)
Note: Award (M1) for correct substitution into area of a sector formula.
OR
(M1)
Note: Award (M1) for correct substitution into curved area of a cone formula.
THEN
(Area) A1
Note: Allow FT from their part (a)(ii) even if their angle is not obtuse.
[2 marks]
Examiners report
Although most candidates understood what to do in part (a), many of them wrote a decimal approximation instead and did not give their answer in terms of as required in this part. Many candidates were able to use the length of arc formula in (a)(ii). Some candidates went wrong with this question by confusing between the two values: and for the radius. In part (b), although candidates were able to find the surface area of the outside of the hat, several added the surface area of the base to their calculation. A few candidates used the cosine rule to find chord which was then used as the circumference of the base of the cone.
Although most candidates understood what to do in part (a), many of them wrote a decimal approximation instead and did not give their answer in terms of as required in this part. Many candidates were able to use the length of arc formula in (a)(ii). Some candidates went wrong with this question by confusing between the two values: and for the radius. In part (b), although candidates were able to find the surface area of the outside of the hat, several added the surface area of the base to their calculation. A few candidates used the cosine rule to find chord which was then used as the circumference of the base of the cone.
Although most candidates understood what to do in part (a), many of them wrote a decimal approximation instead and did not give their answer in terms of as required in this part. Many candidates were able to use the length of arc formula in (a)(ii). Some candidates went wrong with this question by confusing between the two values: and for the radius. In part (b), although candidates were able to find the surface area of the outside of the hat, several added the surface area of the base to their calculation. A few candidates used the cosine rule to find chord which was then used as the circumference of the base of the cone.
There are four stations used by the fire wardens in a national forest.
On the following Voronoi diagram, the coordinates of the stations are and where distances are measured in kilometres.
The dotted lines represent the boundaries of the regions patrolled by the fire warden at each station. The boundaries meet at and .
To reduce the areas of the regions that the fire wardens patrol, a new station is to be built within the quadrilateral . The new station will be located so that it is as far as possible from the nearest existing station.
The Voronoi diagram is to be updated to include the region around the new station at . The edges defined by the perpendicular bisectors of and have been added to the following diagram.
Show that the new station should be built at .
Write down the equation of the perpendicular bisector of .
Hence draw the missing boundaries of the region around on the following diagram.
Markscheme
(the best placement is either point or point )
attempt at using the distance formula (M1)
OR
OR
OR
OR
OR
( or or ) AND
( or or ) A1
OR (or or ) is greater than (or or ) A1
point is the furthest away AG
Note: Follow through from their values provided their (or or ) is greater than their (or or ).
[3 marks]
A1
[1 mark]
A1A1
Note: Award A1 for each correct straight line. Do not FT from their part (b)(i).
[1 mark]
Examiners report
In part (a) many candidates realized that distances were required. Many candidates seemed to have an idea about Voronoi diagrams. However, several candidates did not realize that they had to consider point as well in their comparison. Hence, several candidates only calculated distances from . The numerical comparison of the distance from and from need to be clearly shown. It was a pity to see that some candidates lost marks due to incorrect rounding of the values to three significant figures. The most common error being . In part (b)(i) not many candidates seemed to understand what was required. A significant number of candidates wrote down the equation of the line through , , rather than the required line. In part (b)(ii), it seemed that much time was lost as many candidates attempted to find the equation of the perpendicular bisector of to draw the boundaries.
In part (a) many candidates realized that distances were required. Many candidates seemed to have an idea about Voronoi diagrams. However, several candidates did not realize that they had to consider point as well in their comparison. Hence, several candidates only calculated distances from . The numerical comparison of the distance from and from need to be clearly shown. It was a pity to see that some candidates lost marks due to incorrect rounding of the values to three significant figures. The most common error being . In part (b)(i) not many candidates seemed to understand what was required. A significant number of candidates wrote down the equation of the line through , , rather than the required line. In part (b)(ii), it seemed that much time was lost as many candidates attempted to find the equation of the perpendicular bisector of to draw the boundaries.
In part (a) many candidates realized that distances were required. Many candidates seemed to have an idea about Voronoi diagrams. However, several candidates did not realize that they had to consider point as well in their comparison. Hence, several candidates only calculated distances from . The numerical comparison of the distance from and from need to be clearly shown. It was a pity to see that some candidates lost marks due to incorrect rounding of the values to three significant figures. The most common error being . In part (b)(i) not many candidates seemed to understand what was required. A significant number of candidates wrote down the equation of the line through , , rather than the required line. In part (b)(ii), it seemed that much time was lost as many candidates attempted to find the equation of the perpendicular bisector of to draw the boundaries.
The front view of a doghouse is made up of a square with an isosceles triangle on top.
The doghouse is high and wide, and sits on a square base.
The top of the rectangular surfaces of the roof of the doghouse are to be painted.
Find the area to be painted.
Markscheme
height of triangle at roof (A1)
Note: Award A1 for (height of triangle) seen on the diagram.
OR (M1)
A1
Note: If using then (A1) for angle of , (M1) for a correct trig statement.
area of one rectangle on roof M1
area painted
A1
[5 marks]
Examiners report
Although the first question on the paper, with appropriate low-level mathematics, the interpretation required seems to have been quite high, and many candidates found this challenging. Many candidates scored only the one mark for the height of the triangle. The most common wrong method seen was calculation of the area of the triangle and adding their result to the calculation 2 × 0.9 × 0.9. Stronger candidates lost the final mark either through premature rounding or incorrect units; both are aspects that can and do occur throughout candidate responses and hence clearly require focus in the classroom.
The owner of a convenience store installs two security cameras, represented by points and . Both cameras point towards the centre of the store’s cash register, represented by the point .
The following diagram shows this information on a cross-section of the store.
The cameras are positioned at a height of , and the horizontal distance between the cameras is . The cash register is sitting on a counter so that its centre, , is above the floor.
The distance from Camera to the centre of the cash register is .
Determine the angle of depression from Camera to the centre of the cash register. Give your answer in degrees.
Calculate the distance from Camera to the centre of the cash register.
Without further calculation, determine which camera has the largest angle of depression to the centre of the cash register. Justify your response.
Markscheme
OR (M1)
A1
[2 marks]
METHOD 1
OR OR (M1)
Note: Award M1 for attempt to use Pythagorean Theorem with seen or for attempt to use cosine or tangent ratio.
(A1)
Note: Award the M1A1 if is seen in part (a).
(A1)
Note: Award A1 for or equivalent seen, either as a separate calculation or in Pythagorean Theorem.
A1
METHOD 2
attempt to use cosine rule (M1)
(A1)(A1)
Note: Award A1 for substituted into cosine rule formula, A1 for correct substitution.
A1
[4 marks]
camera is closer to the cash register (than camera and both cameras are at the same height on the wall) R1
the larger angle of depression is from camera A1
Note: Do not award R0A1. Award R0A0 if additional calculations are completed and used in their justification, as per the question. Accept “” or “” as evidence for the R1.
[2 marks]
Examiners report
Many candidates calculated the angle from vertical rather than the angle of depression.
Candidates could successfully use their vertical angle from (a) or other correct trigonometry, such as Pythagorean theorem or cosine rule, to find the distance from camera 2 to the cash register. This question is a good example of how premature rounding can affect a final answer, and some had an inaccurate final answer because they had rounded intermediate values.
Many provided reasonable justification for their response, even though they often followed correct reasoning with an incorrect conclusion about the larger angle of depression.
An inclined railway travels along a straight track on a steep hill, as shown in the diagram.
The locations of the stations on the railway can be described by coordinates in reference to , and -axes, where the and axes are in the horizontal plane and the -axis is vertical.
The ground level station has coordinates and station , located near the top of the hill, has coordinates . All coordinates are given in metres.
Station is to be built halfway between stations and .
Find the distance between stations and .
Find the coordinates of station .
Write down the height of station , in metres, above the ground.
Markscheme
attempt at substitution into 3D distance formula (M1)
A1
[2 marks]
attempt at substitution in the midpoint formula (M1)
A1
[2 marks]
A1
[1 mark]
Examiners report
Points A(3, 1), B(3, 5), C(11, 7), D(9, 1) and E(7, 3) represent snow shelters in the Blackburn National Forest. These snow shelters are illustrated in the following coordinate axes.
Horizontal scale: 1 unit represents 1 km.
Vertical scale: 1 unit represents 1 km.
The Park Ranger draws three straight lines to form an incomplete Voronoi diagram.
Calculate the gradient of the line segment AE.
Find the equation of the line which would complete the Voronoi cell containing site E.
Give your answer in the form where , , .
In the context of the question, explain the significance of the Voronoi cell containing site E.
Markscheme
(M1)
= 0.5 A1
[2 marks]
(A1) (M1)
Note: Award (A1) for their −2 seen, award (M1) for the correct substitution of (5, 2) and their normal gradient in equation of a line.
A1
[3 marks]
every point in the cell is closer to E than any other snow shelter A1
[1 mark]
Examiners report
A garden includes a small lawn. The lawn is enclosed by an arc of a circle with centre and radius , such that . The straight border of the lawn is defined by chord .
The lawn is shown as the shaded region in the following diagram.
A footpath is to be laid around the curved side of the lawn. Find the length of the footpath.
Find the area of the lawn.
Markscheme
(M1)(A1)
A1
[3 marks]
evidence of splitting region into two areas (M1)
(M1)(M1)
Note: Award M1 for correctly substituting into area of sector formula, M1 for evidence of substituting into area of triangle formula.
A1
[4 marks]
Examiners report
Ollie has installed security lights on the side of his house that are activated by a sensor. The sensor is located at point C directly above point D. The area covered by the sensor is shown by the shaded region enclosed by triangle ABC. The distance from A to B is 4.5 m and the distance from B to C is 6 m. Angle AĈB is 15°.
Find CÂB.
Point B on the ground is 5 m from point E at the entrance to Ollie’s house. He is 1.8 m tall and is standing at point D, below the sensor. He walks towards point B.
Find the distance Ollie is from the entrance to his house when he first activates the sensor.
Markscheme
(M1)(A1)
CÂB = 20.2º (20.187415…) A1
Note: Award (M1) for substituted sine rule formula and award (A1) for correct substitutions.
[3 marks]
A1
(let X be the point on BD where Ollie activates the sensor)
(M1)
Note: Award A1 for their correct angle . Award M1 for correctly substituted trigonometric formula.
A1
(M1)
= 2.45 (m) (2.44714…) A1
[5 marks]
Examiners report
The diagram below is part of a Voronoi diagram.
Diagram not to scale
A and B are sites with B having the co-ordinates of (4, 6). L is an edge; the equation of this perpendicular bisector of the line segment from A to B is
Find the co-ordinates of the point A.
Markscheme
Line from A to B will have the form M1A1
Through so line is M1A1
Intersection of and is (2, 5) M1A1
Let then M1A1A1
[9 marks]
Examiners report
The Bermuda Triangle is a region of the Atlantic Ocean with Miami , Bermuda , and San Juan as vertices, as shown on the diagram.
The distances between , and are given in the following table, correct to three significant figures.
Calculate the value of , the measure of angle .
Find the area of the Bermuda Triangle.
Markscheme
attempt at substituting the cosine rule formula (M1)
(A1)
(accept rad ) A1
[3 marks]
correctly substituted area of triangle formula (M1)
A1
Note: Accept from use of . Other angles and their corresponding sides may be used.
[2 marks]
Examiners report
Most candidates were successful at selecting the cosine rule formula in part (a). In most cases, the cosine rule formula was correctly substituted. Some candidates found it hard to choose the correct side to obtain the required angle. Most of the candidates scored one or two marks out of three in this part. In part (b) some candidates assumed the triangle was right angled and used instead of . In part (b) many candidates who answered part (a) incorrectly were able to recover. Many candidates managed to score full marks in this part despite an incorrect answer in part (a). Some found angle or in part (a) but used the correct sides to obtain the correct area. Final answers given in calculator notations (such as ) scored at most one mark out of two. Calculator notation should generally be avoided; it is considered too informal to earn A marks, and although it can imply a method and earn M marks, we advise that candidates still provide the necessary commentary to support any GDC notation.
Most candidates were successful at selecting the cosine rule formula in part (a). In most cases, the cosine rule formula was correctly substituted. Some candidates found it hard to choose the correct side to obtain the required angle. Most of the candidates scored one or two marks out of three in this part. In part (b) some candidates assumed the triangle was right angled and used instead of . In part (b) many candidates who answered part (a) incorrectly were able to recover. Many candidates managed to score full marks in this part despite an incorrect answer in part (a). Some found angle or in part (a) but used the correct sides to obtain the correct area. Final answers given in calculator notations (such as ) scored at most one mark out of two. Calculator notation should generally be avoided; it is considered too informal to earn A marks, and although it can imply a method and earn M marks, we advise that candidates still provide the necessary commentary to support any GDC notation.
Let and , where O is the origin. L1 is the line that passes through A and B.
Find a vector equation for L1.
The vector is perpendicular to . Find the value of p.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
any correct equation in the form r = a + tb (accept any parameter for t)
where a is , and b is a scalar multiple of A2 N2
eg r = , r = 2i + j + 3k + s(i + 3j + k)
Note: Award A1 for the form a + tb, A1 for the form L = a + tb, A0 for the form r = b + ta.
[2 marks]
METHOD 1
correct scalar product (A1)
eg (1 × 2) + (3 × p) + (1 × 0), 2 + 3p
evidence of equating their scalar product to zero (M1)
eg a•b = 0, 2 + 3p = 0, 3p = −2
A1 N3
METHOD 2
valid attempt to find angle between vectors (M1)
correct substitution into numerator and/or angle (A1)
eg
A1 N3
[3 marks]
Examiners report
The position vectors of points P and Q are i 2 j k and 7i 3j 4k respectively.
Find a vector equation of the line that passes through P and Q.
The line through P and Q is perpendicular to the vector 2i nk. Find the value of .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
valid attempt to find direction vector (M1)
eg
correct direction vector (or multiple of) (A1)
eg6i j 3k
any correct equation in the form r a tb (any parameter for ) A2 N3
where a is i 2j k or 7i 3j 4k , and b is a scalar multiple of 6i j 3k
egr 7i 3j 4k t(6i j 3k), r
Notes: Award A1 for the form a tb, A1 for the form L a tb, A0 for the form r b ta.
[4 marks]
correct expression for scalar product (A1)
eg
setting scalar product equal to zero (seen anywhere) (M1)
egu v
A1 N2
[3 marks]
Examiners report
Money boxes are coin containers used by children and come in a variety of shapes. The money box shown is in the shape of a cylinder. It has a radius of 4.43 cm and a height of 12.2 cm.
Find the volume of the money box.
A second money box is in the shape of a sphere and has the same volume as the cylindrical money box.
Find the diameter of the second money box.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(V =) (M1)(A1)
Note: Award (M1) for substitution into volume of a cylinder formula, (A1) for correct substitution.
752 cm3 (752.171…cm3) (A1)(C3)
[3 marks]
(M1)
Note: Award (M1) for equating their volume to the volume of a sphere formula.
5.64169…cm (A1)(ft)
Note: Follow through from part (a).
11.3 cm (11.2833…cm) (A1)(ft) (C3)
[3 marks]
Examiners report
A solid right circular cone has a base radius of 21 cm and a slant height of 35 cm.
A smaller right circular cone has a height of 12 cm and a slant height of 15 cm, and is removed from the top of the larger cone, as shown in the diagram.
Calculate the radius of the base of the cone which has been removed.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(M1)
Note: Award (M1) for correct substitution into Pythagoras theorem.
OR
(M1)
Note: Award (M1) for a correct equation.
= 9 (cm) (A1) (C2)
[2 marks]
Examiners report
Emily’s kite ABCD is hanging in a tree. The plane ABCDE is vertical.
Emily stands at point E at some distance from the tree, such that EAD is a straight line and angle BED = 7°. Emily knows BD = 1.2 metres and angle BDA = 53°, as shown in the diagram

T is a point at the base of the tree. ET is a horizontal line. The angle of elevation of A from E is 41°.
Find the length of EB.
Write down the angle of elevation of B from E.
Find the vertical height of B above the ground.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
Units are required in parts (a) and (c).
(M1)(A1)
Note: Award (M1) for substitution into sine formula, (A1) for correct substitution.
OROR (A1) (C3)
[3 marks]
34° (A1) (C1)
[1 mark]
Units are required in parts (a) and (c).
(M1)
Note: Award (M1) for correct substitution into a trigonometric ratio.
OROR (A1)(ft) (C2)
Note: Accept “BT” used for height. Follow through from parts (a) and (b). Use of 7.86 gives an answer of 4.39525….
[2 marks]
Examiners report
A vertical pole stands on horizontal ground. The bottom of the pole is taken as the origin, , of a coordinate system in which the top, , of the pole has coordinates . All units are in metres.
The pole is held in place by ropes attached at .
One of the ropes is attached to the ground at a point with coordinates . The rope forms a straight line from to .
Find the length of the rope connecting to .
Find , the angle the rope makes with the ground.
Markscheme
(M1)
A1
[2 marks]
OR OR (M1)
A1
[2 marks]
Examiners report
This question was the first of its type to be tested and the problem was reduced (erroneously) to 2D trigonometry. Whilst a minority of candidates did tackle this part correctly, many simply arrived at an incorrect length with metres.
The incorrect interpretation of the diagram as being 2D, meant that there was an assumption that OA was of length 3.2 metres and so ° was seen on many scripts. If, using their incorrect answer for part (a), the candidate had used it was possible to award “follow through” marks.
The straight metal arm of a windscreen wiper on a car rotates in a circular motion from a pivot point, , through an angle of . The windscreen is cleared by a rubber blade of length that is attached to the metal arm between points and . The total length of the metal arm, , is .
The part of the windscreen cleared by the rubber blade is shown unshaded in the following diagram.
Calculate the length of the arc made by , the end of the rubber blade.
Determine the area of the windscreen that is cleared by the rubber blade.
Markscheme
attempt to substitute into length of arc formula (M1)
A1
[2 marks]
subtracting two substituted area of sectors formulae (M1)
OR (A1)
A1
[3 marks]
Examiners report
There was some difficulty determining the correct radius to substitute, with several candidates substituting a radius of 46.
It was common to see candidates subtracting the radii before substituting into the area formula, rather than subtracting the sector areas after calculating each. Using the π key on the calculator rather than an approximated value was prevalent and pleasing to see.
A cylinder with radius and height is shown in the following diagram.
The sum of and for this cylinder is 12 cm.
Write down an equation for the area, , of the curved surface in terms of .
Find .
Find the value of when the area of the curved surface is maximized.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
OR (A1)(M1) (C2)
Note: Award (A1) for or seen. Award (M1) for correctly substituting into curved surface area of a cylinder. Accept OR .
[2 marks]
(A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for and (A1)(ft) for . Follow through from part (a). Award at most (A1)(ft)(A0) if additional terms are seen.
[2 marks]
(M1)
Note: Award (M1) for setting their part (b) equal to zero.
6 (cm) (A1)(ft) (C2)
Note: Follow through from part (b).
[2 marks]
Examiners report
A balloon in the shape of a sphere is filled with helium until the radius is 6 cm.
The volume of the balloon is increased by 40%.
Calculate the volume of the balloon.
Calculate the radius of the balloon following this increase.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
Units are required in parts (a) and (b).
(M1)
Note: Award (M1) for correct substitution into volume of sphere formula.
(A1) (C2)
Note: Answers derived from the use of approximations of (3.14; 22/7) are awarded (A0).
[2 marks]
Units are required in parts (a) and (b).
OR OR (M1)(M1)
Note: Award (M1) for multiplying their part (a) by 1.4 or equivalent, (M1) for equating to the volume of a sphere formula.
OR OR OR (M1)
Note: Award (M1) for isolating .
(A1)(ft) (C4)
Note: Follow through from part (a).
[4 marks]
Examiners report
Let be an obtuse angle such that .
Let .
Find the value of .
Line passes through the origin and has a gradient of . Find the equation of .
Find the derivative of .
The following diagram shows the graph of for 0 ≤ ≤ 3. Line is a tangent to the graph of at point P.
Given that is parallel to , find the -coordinate of P.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
evidence of valid approach (M1)
eg sketch of triangle with sides 3 and 5,
correct working (A1)
eg missing side is 4 (may be seen in sketch), ,
A2 N4
[4 marks]
correct substitution of either gradient or origin into equation of line (A1)
(do not accept )
eg , ,
A2 N4
Note: Award A1A0 for .
[2 marks]
(seen anywhere, including answer) A1
choosing product rule (M1)
eg
correct derivatives (must be seen in a correct product rule) A1A1
eg ,
A1 N5
[5 marks]
valid approach to equate their gradients (M1)
eg , , ,
correct equation without (A1)
eg , ,
correct working (A1)
eg ,
(do not accept ) A1 N1
Note: Do not award the final A1 if additional answers are given.
[4 marks]
Examiners report
Two schools are represented by points and on the graph below. A road, represented by the line with equation , passes near the schools. An architect is asked to determine the location of a new bus stop on the road such that it is the same distance from the two schools.
Find the equation of the perpendicular bisector of . Give your equation in the form .
Determine the coordinates of the point on where the bus stop should be located.
Markscheme
gradient (A1)
midpoint (A1)
gradient of bisector (M1)
perpendicular bisector: OR (M1)
perpendicular bisector: A1
[5 marks]
attempt to solve simultaneous equations (M1)
A1
[2 marks]
Examiners report
A line, , has equation . Point lies on .
Find .
A second line, , is parallel to and passes through (1, 2, 3).
Write down a vector equation for .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
correct equation (A1)
eg ,
(A1)
substitute their value into component (M1)
eg ,
A1 N3
[4 marks]
(=(i + 2j + 3k) + (6i + 2k)) A2 N2
Note: Accept any scalar multiple of for the direction vector.
Award A1 for , A1 for , A0 for .
[2 marks]
Examiners report
Point A has coordinates (−4, −12, 1) and point B has coordinates (2, −4, −4).
The line L passes through A and B.
Show that
Find a vector equation for L.
Point C (k , 12 , −k) is on L. Show that k = 14.
Find .
Write down the value of angle OBA.
Point D is also on L and has coordinates (8, 4, −9).
Find the area of triangle OCD.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
correct approach A1
eg
AG N0
[1 mark]
any correct equation in the form r = a + tb (any parameter for t) A2 N2
where a is or and b is a scalar multiple of
eg r r
Note: Award A1 for the form a + tb, A1 for the form L = a + tb, A0 for the form r = b + ta.
[2 marks]
METHOD 1 (solving for t)
valid approach (M1)
eg
one correct equation A1
eg −4 + 8t = 12, −12 + 8t = 12
correct value for t (A1)
eg t = 2 or 3
correct substitution A1
eg 2 + 6(2), −4 + 6(3), −[1 + 3(−5)]
k = 14 AG N0
METHOD 2 (solving simultaneously)
valid approach (M1)
eg
two correct equations in A1
eg k = −4 + 6t, −k = 1 −5t
EITHER (eliminating k)
correct value for t (A1)
eg t = 2 or 3
correct substitution A1
eg 2 + 6(2), −4 + 6(3)
OR (eliminating t)
correct equation(s) (A1)
eg 5k + 20 = 30t and −6k − 6 = 30t, −k = 1 − 5
correct working clearly leading to k = 14 A1
eg −k + 14 = 0, −6k = 6 −5k − 20, 5k = −20 + 6(1 + k)
THEN
k = 14 AG N0
[4 marks]
correct substitution into scalar product A1
eg (2)(6) − (4)(8) − (4)(−5), 12 − 32 + 20
= 0 A1 N0
[2 marks]
A1 N1
[1 marks]
METHOD 1 ( × height × CD)
recognizing that OB is altitude of triangle with base CD (seen anywhere) M1
eg sketch showing right angle at B
or (seen anywhere) (A1)
correct magnitudes (seen anywhere) (A1)(A1)
correct substitution into A1
eg
area A1 N3
METHOD 2 (subtracting triangles)
recognizing that OB is altitude of either ΔOBD or ΔOBC(seen anywhere) M1
eg sketch of triangle showing right angle at B
one correct vector or or or (seen anywhere) (A1)
eg ,
(seen anywhere) (A1)
one correct magnitude of a base (seen anywhere) (A1)
correct working A1
eg
area A1 N3
METHOD 3 (using ab sin C with ΔOCD)
two correct side lengths (seen anywhere) (A1)(A1)
attempt to find cosine ratio (seen anywhere) M1
eg
correct working for sine ratio A1
eg
correct substitution into A1
eg
area A1 N3
[6 marks]
Examiners report
A solid glass paperweight consists of a hemisphere of diameter 6 cm on top of a cuboid with a square base of length 6 cm, as shown in the diagram.
The height of the cuboid, x cm, is equal to the height of the hemisphere.
Write down the value of x.
Calculate the volume of the paperweight.
1 cm3 of glass has a mass of 2.56 grams.
Calculate the mass, in grams, of the paperweight.
Markscheme
3 (cm) (A1) (C1)
[1 mark]
units are required in part (a)(ii)
(M1)(M1)
Note: Award (M1) for their correct substitution in volume of sphere formula divided by 2, (M1) for adding their correctly substituted volume of the cuboid.
= 165 cm3 (164.548…) (A1)(ft) (C3)
Note: The answer is 165 cm3; the units are required. Follow through from part (a)(i).
[3 marks]
their 164.548… × 2.56 (M1)
Note: Award (M1) for multiplying their part (a)(ii) by 2.56.
= 421 (g) (421.244…(g)) (A1)(ft) (C2)
Note: Follow through from part (a)(ii).
[2 marks]
Examiners report
Six equilateral triangles, each with side length 3 cm, are arranged to form a hexagon.
This is shown in the following diagram.
The vectors p , q and r are shown on the diagram.
Find p•(p + q + r).
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
METHOD 1 (using |p| |2q| cosθ)
finding p + q + r (A1)
eg 2q,
| p + q + r | = 2 × 3 (= 6) (seen anywhere) A1
correct angle between p and q (seen anywhere) (A1)
(accept 60°)
substitution of their values (M1)
eg 3 × 6 × cos
correct value for cos (seen anywhere) (A1)
eg
p•(p + q + r) = 9 A1 N3
METHOD 2 (scalar product using distributive law)
correct expression for scalar distribution (A1)
eg p• p + p•q + p•r
three correct angles between the vector pairs (seen anywhere) (A2)
eg 0° between p and p, between p and q, between p and r
Note: Award A1 for only two correct angles.
substitution of their values (M1)
eg 3.3.cos0 +3.3.cos + 3.3.cos120
one correct value for cos0, cos or cos (seen anywhere) A1
eg
p•(p + q + r) = 9 A1 N3
METHOD 3 (scalar product using relative position vectors)
valid attempt to find one component of p or r (M1)
eg sin 60 = , cos 60 = , one correct value
one correct vector (two or three dimensions) (seen anywhere) A1
eg
three correct vectors p + q + r = 2q (A1)
p + q + r = or (seen anywhere, including scalar product) (A1)
correct working (A1)
eg
p•(p + q + r) = 9 A1 N3
[6 marks]
Examiners report
A line passes through points and .
The line also passes through the point .
Show that .
Find a vector equation for .
Find the value of .
The point D has coordinates . Given that is perpendicular to , find the possible values of .
Markscheme
correct approach A1
eg
AG N0
[1 mark]
any correct equation in the form (any parameter for )
where is or and is a scalar multiple of A2 N2
eg
Note: Award A1 for the form , A1 for the form , A0 for the form .
[2 marks]
METHOD 1 – finding value of parameter
valid approach (M1)
eg
one correct equation (not involving ) (A1)
eg
correct parameter from their equation (may be seen in substitution) A1
eg
correct substitution (A1)
eg
A1 N2
METHOD 2 – eliminating parameter
valid approach (M1)
eg
one correct equation (not involving ) (A1)
eg
correct equation (with ) A1
eg
correct working to solve for (A1)
eg
A1 N2
[5 marks]
valid approach to find or (M1)
eg
correct vector for or (may be seen in scalar product) A1
eg
recognizing scalar product of or with direction vector of is zero (seen anywhere) (M1)
eg
correct scalar product in terms of only A1
eg
correct working to solve quadratic (A1)
eg
A1A1 N3
[7 marks]
Examiners report
Consider the vectors a = and b = .
Find the value of for which a and b are
parallel.
perpendicular.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
valid approach (M1)
eg b = 2a, a = b, cos θ = 1, a•b = −|a||b|, 2 = 18
= 9 A1 N2
[2 marks]
evidence of scalar product (M1)
eg a•b, (0)(0) + (3)(6) + (18)
recognizing a•b = 0 (seen anywhere) (M1)
correct working (A1)
eg 18 + 18 = 0, 18 = −18 (A1)
= −1 A1 N3
[4 marks]
Examiners report
Yao drains the oil from his motorbike into two identical cuboids with rectangular bases of width cm and length cm. The height of each cuboid is cm.
The oil from the motorbike fills the first cuboid completely and the second cuboid to a height of cm. The information is shown in the following diagram.
Calculate the volume of oil drained from Yao’s motorbike.
Yao then pours all the oil from the cuboids into an empty cylindrical container. The height of the oil in the container is cm.
Find the internal radius, , of the container.
Markscheme
units are required in both parts
(M1)(M1)
Note: Award (M1) for correct substitutions in volume formula for both cuboids. Award (M1) for adding the volumes of both cuboids.
cm3 (A1) (C3)
[3 marks]
units are required in both parts
(M1)(M1)
Note: Award (M1) for correct substitution in volume of cylinder formula. Award (M1) for equating their expression (must include and ) to their .
cm (… cm) (A1)(ft) (C3)
Note: Follow through from their part (a).
[3 marks]
Examiners report
The following diagram shows triangle ABC, with , , and .
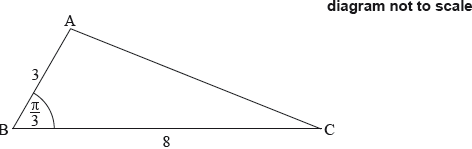
Show that .
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
evidence of choosing the cosine rule (M1)
eg
correct substitution into RHS of cosine rule (A1)
eg
evidence of correct value for (may be seen anywhere, including in cosine rule) A1
eg
correct working clearly leading to answer A1
eg
AG N0
Note: Award no marks if the only working seen is or (or similar).
[4 marks]
correct substitution for semicircle (A1)
eg
valid approach (seen anywhere) (M1)
eg
A1 N2
[3 marks]
Examiners report
A buoy is floating in the sea and can be seen from the top of a vertical cliff. A boat is travelling from the base of the cliff directly towards the buoy.
The top of the cliff is 142 m above sea level. Currently the boat is 100 metres from the buoy and the angle of depression from the top of the cliff to the boat is 64°.
Draw and label the angle of depression on the diagram.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1) (C1)
Note: The horizontal line must be shown and the angle of depression must be labelled. Accept a numerical or descriptive label.
[1 mark]
Examiners report
Helen is building a cabin using cylindrical logs of length 2.4 m and radius 8.4 cm. A wedge is cut from one log and the cross-section of this log is illustrated in the following diagram.
Find the volume of this log.
Markscheme
volume M1M1M1
Note: Award M1 240 × area, award M1 for correctly substituting area sector formula, award M1 for subtraction of their area of the sector from area of circle.
= 45800 (= 45811.96071) A1
[4 marks]
Examiners report
The magnitudes of two vectors, u and v, are 4 and respectively. The angle between u and v is .
Let w = u − v. Find the magnitude of w.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
METHOD 1 (cosine rule)
diagram including u, v and included angle of (M1)
eg
sketch of triangle with w (does not need to be to scale) (A1)
eg
choosing cosine rule (M1)
eg
correct substitution A1
eg
(seen anywhere) (A1)
correct working (A1)
eg 16 + 3 − 12
| w | = A1 N2
METHOD 2 (scalar product)
valid approach, in terms of u and v (seen anywhere) (M1)
eg | w |2 = (u − v)•(u − v), | w |2 = u•u − 2u•v + v•v, | w |2 = ,
| w | =
correct value for u•u (seen anywhere) (A1)
eg | u |2 = 16, u•u = 16,
correct value for v•v (seen anywhere) (A1)
eg | v |2 = 16, v•v = 3,
(seen anywhere) (A1)
u•v (= 6) (seen anywhere) A1
correct substitution into u•u − 2u•v + v•v or (2 or 3 dimensions) (A1)
eg 16 − 2(6) + 3 (= 7)
| w | = A1 N2
Examiners report
Two fixed points, A and B, are 40 m apart on horizontal ground. Two straight ropes, AP and BP, are attached to the same point, P, on the base of a hot air balloon which is vertically above the line AB. The length of BP is 30 m and angle BAP is 48°.
On the diagram, draw and label with an x the angle of depression of B from P.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1) (C1)
[1 mark]