An ice-skater is skating such that her position vector when viewed from above at time $t$ seconds can be modelled by

$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}a {\text{e}}^{bt}\cos t\\ a {\text{e}}^{bt}\text{\hspace{0.05em}sin} t\end{array}\right)$

with respect to a rectangular coordinate system from a point $\text{O}$, where the non-zero constants $a$ and $b$ can be determined. All distances are in metres.

At time $t=0$, the displacement of the ice-skater is given by $\left(\begin{array}{c}5\\ 0\end{array}\right)$ and the velocity of the ice‑skater is given by $\left(\begin{array}{c}-3.5\\ 5\end{array}\right)$.

Consider the following system of coupled differential equations.

$\frac{dx}{dt}=-4x$

$\frac{dy}{dt}=3x-2y$

Find the value of $\frac{dy}{dx}$

A ball is attached to the end of a string and spun horizontally. Its position relative to a given point, $\text{O}$, at time $t$ seconds, $t\ge 0$, is given by the equation

$\mathit{r}=\left(\begin{array}{c}1.5 \cos (0.1t^2)\\ 1.5 \sin (0.1t^2)\end{array}\right)$ where all displacements are in metres.

The string breaks when the magnitude of the ball’s acceleration exceeds $20 {\text{ms}}^{-2}$.

A change in grazing habits has resulted in two species of herbivore, $\text{X}$ and $\text{Y}$, competing for food on the same grasslands. At time $t=0$ environmentalists begin to record the sizes of both populations. Let the size of the population of $\text{X}$ be $x$, and the size of the population $\text{Y}$ be $y$. The following model is proposed for predicting the change in the sizes of the two populations:

$\dot{x}=0.3x-0.1y$

$\dot{y}=-0.2x+0.4y$

for $x, y>0$

For this system of coupled differential equations find

When $t=0$ $\text{X}$ has a population of $2000$.

It is known that $\text{Y}$ has an initial population of $2900$.

A particle $\text{P}$ moves along the $x$-axis. The velocity of $\text{P}$ is $v{\text{\hspace{0.05em}m\hspace{0.05em}s}}^{-1}$ at time $t$ seconds, where $v=-2t^2+16t-24$ for $t\ge 0$.

A shock absorber on a car contains a spring surrounded by a fluid. When the car travels over uneven ground the spring is compressed and then returns to an equilibrium position.

The displacement, $x$, of the spring is measured, in centimetres, from the equilibrium position of $x=0$. The value of $x$ can be modelled by the following second order differential equation, where $t$ is the time, measured in seconds, after the initial displacement.

$\ddot{x}+3\dot{x}+1.25x=0$

The differential equation can be expressed in the form $\left(\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right)=\mathit{A}\left(\begin{array}{c}x\\ y\end{array}\right)$, where $\mathit{A}$ is a $2\times 2$ matrix.

The cross-sectional view of a tunnel is shown on the axes below. The line $\left[\text{AB}\right]$ represents a vertical wall located at the left side of the tunnel. The height, in metres, of the tunnel above the horizontal ground is modelled by $y=-0.1x^3+ 0.8x^2, 2\le x\le 8$, relative to an origin $\text{O}$.

Point $\text{A}$ has coordinates $(2, 0)$, point $\text{B}$ has coordinates $(2, 2.4)$, and point $\text{C}$ has coordinates $(8, 0)$.

Find the height of the tunnel when

A particle moves such that its displacement, $x$ metres, from a point $\text{O}$ at time $t$ seconds is given by the differential equation

$\frac{d^{2}x}{d{t}^2}+5\frac{dx}{dt}+6x=0$

The equation for the motion of the particle is amended to

$\frac{d^{2}x}{d{t}^2}+5\frac{dx}{dt}+6x=3t+4$.

When $t=0$ the particle is stationary at $\text{O}$.

The curve $y=f\left(x\right)$ is shown in the graph, for $0⩽<!--\; ⩽\; -->x⩽<!--\; ⩽\; -->10$.

The curve $y=f\left(x\right)$ passes through the following points.

It is required to find the area bounded by the curve, the $x$-axis, the $y$-axis and the line $x=10$.

One possible model for the curve $y=f\left(x\right)$ is a cubic function.

At an archery tournament, a particular competition sees a ball launched into the air while an archer attempts to hit it with an arrow.

The path of the ball is modelled by the equation

$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}5\\ 0\end{array}\right)+t\left(\begin{array}{c}{u}_x\\ u_y-5t\end{array}\right)$

where $x$ is the horizontal displacement from the archer and $y$ is the vertical displacement from the ground, both measured in metres, and $t$ is the time, in seconds, since the ball was launched.

• $u_x$ is the horizontal component of the initial velocity
• $u_y$ is the vertical component of the initial velocity.

In this question both the ball and the arrow are modelled as single points. The ball is launched with an initial velocity such that $u_x=8$ and $u_y=10$.

An archer releases an arrow from the point $(0, 2)$. The arrow is modelled as travelling in a straight line, in the same plane as the ball, with speed $60 {\text{m\hspace{0.05em}s}}^{-1}$ and an angle of elevation of $10°$.

A biologist introduces $100$ rabbits to an island and records the size of their population $\left(x\right)$ over a period of time. The population growth of the rabbits can be approximately modelled by the following differential equation, where $t$ is time measured in years.

$\frac{dx}{dt}=2x$

A population of $100$ foxes is introduced to the island when the population of rabbits has reached $1000$. The subsequent population growth of rabbits and foxes, where $y$ is the population of foxes at time $t$, can be approximately modelled by the coupled equations:

$\frac{dx}{dt}=x\left(2-0.01y\right)$

$\frac{dy}{dt}=y\left(0.0002x-0.8\right)$

Use Euler’s method with a step size of $0.25$, to find

The graph of the population sizes, according to this model, for the first $4$ years after the foxes were introduced is shown below.

Describe the changes in the populations of rabbits and foxes for these $4$ years at

Jorge is carefully observing the rise in sales of a new app he has created.

The number of sales in the first four months is shown in the table below.

Jorge believes that the increase is exponential and proposes to model the number of sales $N$ in month $t$ with the equation

$N=A{\text{e}}^{rt}, A, r\in \mathrm{ℝ}$

Jorge plans to adapt Euler’s method to find an approximate value for $r$.

With a step length of one month the solution to the differential equation can be approximated using Euler’s method where

$N\left(n+1\right)\approx N\left(n\right)+1\times N\text{'}\left(n\right), n\in \mathrm{\mathbb{N}}$

Jorge decides to take the mean of these values as the approximation of $r$ for his model. He also decides the graph of the model should pass through the point $(2, 52)$.

The sum of the square residuals for these points for the least squares regression model is approximately $6.555$.

A student investigating the relationship between chemical reactions and temperature finds the Arrhenius equation on the internet.

$k=A{\text{e}}^{-\frac{c}{T}}$

This equation links a variable $k$ with the temperature $T$, where $A$ and $c$ are positive constants and $T>0$.

The Arrhenius equation predicts that the graph of $\ln k$ against $\frac{1}{T}$ is a straight line.

Write down

The following data are found for a particular reaction, where $T$ is measured in Kelvin and $k$ is measured in ${\text{cm}}^3 {\text{mol}}^{-1} {\text{s}}^{-1}$:

Find an estimate of

The voltage $v$ in a circuit is given by the equation

$v\left(t\right)=3\text{sin}\left(100\mathrm{\pi <!--\; \pi \; -->}t\right)$, $t⩾<!--\; ⩾\; -->0$ where $t$ is measured in seconds.

The current $i$ in this circuit is given by the equation

$i\left(t\right)=2\text{sin}\left(100\mathrm{\pi <!--\; \pi \; -->}\left(t+0.003\right)\right)$.

The power $p$ in this circuit is given by $p\left(t\right)=v\left(t\right)\times <!--\; \times \; -->i\left(t\right)$.

The average power $p_{av}$ in this circuit from $t=0$ to $t=T$ is given by the equation

$p_{av}\left(T\right)=\frac{1}{T}{\int <!--\; \int \; -->}_0^{T}p\left(t\right)\text{d}t$, where $T>0$.

Consider the system of paired differential equations

$\stackrel{\dot{}<!--\; \dot{}\; -->}{x}=3x+2y$

$\stackrel{\dot{}<!--\; \dot{}\; -->}{y}=2x+3y$.

This represents the populations of two species of symbiotic toadstools in a large wood.

Time $t$ is measured in decades.

Consider the curve $y=\sqrt{x}$.

The shape of a piece of metal can be modelled by the region bounded by the functions $f$, $g$, the $x$-axis and the line segment $\text{[AB]}$, as shown in the following diagram. The units on the $x$ and $y$ axes are measured in metres.

The piecewise function $f$ is defined by

$f\left(x\right)=\{\begin{array}{cc}\sqrt{x} & 0\le x\le 0.16\\ 1.25x+0.2 & 0.16<x\le 0.5\end{array}$

The graph of $g$ is obtained from the graph of $f$ by:

• a stretch scale factor of $\frac{1}{2}$ in the $x$ direction,
• followed by a stretch scale factor $\frac{1}{2}$ in the $y$ direction,
• followed by a translation of $0.2$ units to the right.

Point $\text{A}$ lies on the graph of $f$ and has coordinates $(0.5, 0.825)$. Point $\text{B}$ is the image of $\text{A}$ under the given transformations and has coordinates $(p, q)$.

The piecewise function $g$ is given by

$g\left(x\right)=\{\begin{array}{cc}h\left(x\right) & 0.2\le x\le a\\ 1.25x+b & a<x\le p\end{array}$

The area enclosed by $y=g\left(x\right)$, the $x$-axis and the line $x=p$ is $0.0627292 {\text{m}}^2$ correct to six significant figures.

A sector of a circle, centre $\text{O}$ and radius $4.5 \text{m}$, is shown in the following diagram.

A square field with side $8 \text{m}$ has a goat tied to a post in the centre by a rope such that the goat can reach all parts of the field up to $4.5 \text{m}$ from the post.

^{[Source: mynamepong, n.d. Goat [image online] Available at: https://thenounproject.com/term/goat/1761571/
This file is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)
https://creativecommons.org/licenses/by-sa/3.0/deed.en [Accessed 22 April 2010] Source adapted.]}

Let $V$ be the volume of grass eaten by the goat, in cubic metres, and $t$ be the length of time, in hours, that the goat has been in the field.

The goat eats grass at the rate of $\frac{dV}{dt}=0.3 t{\text{e}}^{-t}$.

Consider the function .

Consider the region bounded by the curve $y=f(x)$, the $x$-axis and the lines $x=\frac{\mathrm{\pi <!--\; \pi \; -->}}{6},x=\frac{\mathrm{\pi <!--\; \pi \; -->}}{3}$.

An environmental scientist is asked by a river authority to model the effect of a leak from a power plant on the mercury levels in a local river. The variable $x$ measures the concentration of mercury in micrograms per litre.

The situation is modelled using the second order differential equation

$\frac{{\text{d}}^{2}x}{d{t}^2}+3\frac{dx}{dt}+2x=0$

where $t\ge 0$ is the time measured in days since the leak started. It is known that when $t=0, x=0$ and $\frac{dx}{dt}=1$.

If the mercury levels are greater than $0.1$ micrograms per litre, fishing in the river is considered unsafe and is stopped.

The river authority decides to stop people from fishing in the river for $10\%$ longer than the time found from the model.

A water trough which is 10 metres long has a uniform cross-section in the shape of a semicircle with radius 0.5 metres. It is partly filled with water as shown in the following diagram of the cross-section. The centre of the circle is O and the angle KOL is $\mathrm{\theta <!--\; \theta \; -->}$ radians.

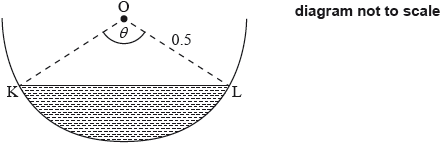
The volume of water is increasing at a constant rate of $0.0008{\text{m}}^3{\text{s}}^{-<!--\; -\; -->1}$.

Charlotte decides to model the shape of a cupcake to calculate its volume.

From rotating a photograph of her cupcake she estimates that its cross-section passes through the points $(0, 3.5), (4, 6), (6.5, 4), (7, 3)$ and $(7.5, 0)$, where all units are in centimetres. The cross-section is symmetrical in the $x$-axis, as shown below:

She models the section from $(0, 3.5)$ to $(4, 6)$ as a straight line.

Charlotte models the section of the cupcake that passes through the points $(4, 6), (6.5, 4), (7, 3)$ and $(7.5, 0)$ with a quadratic curve.

Charlotte thinks that a quadratic with a maximum point at $(4, 6)$ and that passes through the point $(7.5, 0)$ would be a better fit.

Believing this to be a better model for her cupcake, Charlotte finds the volume of revolution about the $x$-axis to estimate the volume of the cupcake.

Consider $f(x)=-<!--\; -\; -->1+\ln <!--\; \; -->\left(\sqrt{x^2-<!--\; -\; -->1}\right)$

The function $f$ is defined by $f(x)=-<!--\; -\; -->1+\ln <!--\; \; -->\left(\sqrt{x^2-<!--\; -\; -->1}\right),x\in <!--\; \in \; -->D$

The function $g$ is defined by $g(x)=-<!--\; -\; -->1+\ln <!--\; \; -->\left(\sqrt{x^2-<!--\; -\; -->1}\right),x\in <!--\; \in \; -->\left]1,\mathrm{\infty <!--\; \infty \; -->}\right[$.

Consider the function .

Let $u=\tan <!--\; \; -->x$.

A point P moves in a straight line with velocity $v$ ms⁻¹ given by $v\left(t\right)={\text{e}}^{-<!--\; -\; -->t}-<!--\; -\; -->8t^2{\text{e}}^{-<!--\; -\; -->2t}$ at time t seconds, where t ≥ 0.

A curve C is given by the implicit equation $x+y-<!--\; -\; -->\text{cos}\left(xy\right)=0$.

The curve $xy=-<!--\; -\; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{2}$ intersects C at P and Q.

The following graph shows the two parts of the curve defined by the equation $x^{2}y=5-<!--\; -\; -->y^4$, and the normal to the curve at the point P(2 , 1).

Xavier, the parachutist, jumps out of a plane at a height of $h$ metres above the ground. After free falling for 10 seconds his parachute opens. His velocity, $v\text{m}{\text{s}}^{-<!--\; -\; -->1}$, $t$ seconds after jumping from the plane, can be modelled by the function

His velocity when he reaches the ground is $2.8\text{ m}{\text{s}}^{-<!--\; -\; -->1}$.

The region $A$ is enclosed by the graph of $y=2\arcsin <!--\; \; -->(x-<!--\; -\; -->1)-<!--\; -\; -->\frac{\mathrm{\pi <!--\; \pi \; -->}}{4}$, the $y$-axis and the line $y=\frac{\mathrm{\pi <!--\; \pi \; -->}}{4}$.

The curve $C$ is defined by equation $xy-<!--\; -\; -->\ln <!--\; \; -->y=1,y>0$.

An object is placed into the top of a long vertical tube, filled with a thick viscous fluid, at time $t=0$ seconds.

Initially it is thought that the resistance of the fluid would be proportional to the velocity of the object. The following model was proposed, where the object’s displacement, $x$, from the top of the tube, measured in metres, is given by the differential equation

$\frac{{\text{d}}^{2}x}{\text{d}{t}^2}=9.81-<!--\; -\; -->0.9\left(\frac{\text{d}x}{\text{d}t}\right)$.

The maximum velocity approached by the object as it falls is known as the terminal velocity.

An experiment is performed in which the object is placed in the fluid on a number of occasions and its terminal velocity recorded. It is found that the terminal velocity was consistently smaller than that predicted by the model used. It was suggested that the resistance to motion is actually proportional to the velocity squared and so the following model was set up.

$$\frac{{\text{d}}^{2}x}{\text{d}{t}^2}=9.81-<!--\; -\; -->0.9{\left(\frac{\text{d}x}{\text{d}t}\right)}^2$$

At terminal velocity the acceleration of an object is equal to zero.

The function $f$ is defined by $f\left(x\right)=\frac{2\text{ln}x+1}{x-<!--\; -\; -->3}$, 0 < $x$ < 3.

Draw a set of axes showing $x$ and $y$ values between −3 and 3. On these axes